As duas tarefas do aprendizado supervisionado: regressão e classificação. Regressão linear, funções de perda e a descida do gradiente.

De Vishal Maini. 19 de agosto de 2019.

Esta série está disponível como um e-book completo! Baixe aqui. Gratuito para baixar; aprecio contribuições (paypal.me/ml4h).

Quanto dinheiro ganharemos gastando mais com publicidade digital? Este solicitante de empréstimo pagará o empréstimo ou não? O que vai acontecer com o mercado de ações amanhã?

Em problemas de aprendizado supervisionado, começamos com um conjunto de dados que contêm exemplos de treinamento com rótulos corretos associados. Por exemplo, ao aprender a classificar dígitos manuscritos, um algoritmo de aprendizado supervisionado recebe milhares de imagens de dígitos manuscritos junto com rótulos que contêm o número correto que cada imagem representa. O algoritmo aprenderá então a relação entre as imagens e seus números associados e aplicará essa relação aprendida para classificar imagens completamente novas (sem rótulos) que a máquina nunca viu antes. É assim que você pode depositar um cheque tirando uma foto com seu celular!

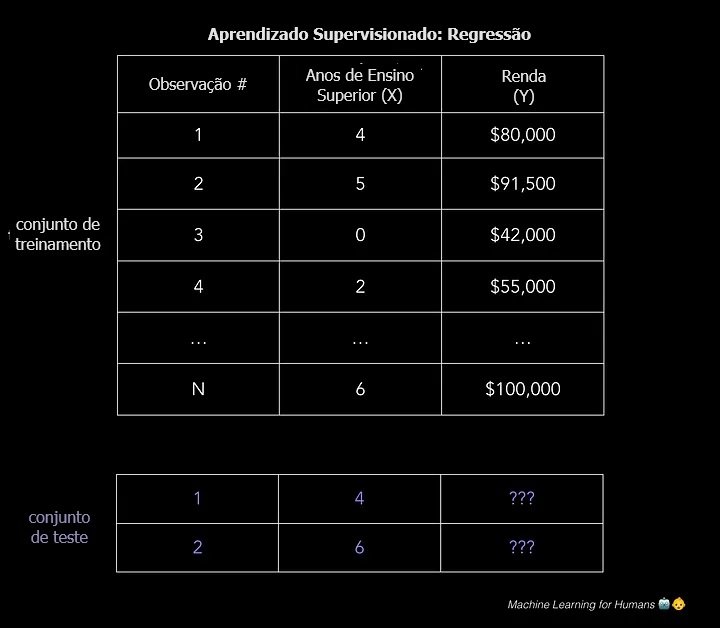
Para ilustrar como funciona o aprendizado supervisionado, vamos examinar o problema de prever a renda anual com base no número de anos de ensino superior que alguém completou. Expresando isso de forma mais formal, gostaríamos de construir um modelo que se aproxime da relação f entre o número de anos de ensino superior X e a renda anual correspondente Y .

X (entrada) = anos de ensino superior Y (saída) = renda anual f = função que descreve a relação entre X e Y ϵ (épsilon) = termo de erro aleatório (positivo ou negativo) com média zero Com relação a épsilon: (1) ϵ representa erro irredutível no modelo, que é um limite teórico em torno do desempenho do seu algoritmo devido ao ruído inerente aos fenômenos que você está tentando explicar. Por exemplo, imagine construir um modelo para prever o resultado de um lançamento de moeda. (2) Aliás, o matemático Paul Erdős referiu-se às crianças como “épsilons” porque em cálculo (mas não em estatística!) ϵ denota uma quantidade positiva arbitrariamente pequena. Adequado, não?

Um método para prever a renda seria criar um modelo rígido baseado em regras sobre como a renda e a educação estão relacionadas. Por exemplo: “Eu estimaria que, para cada ano adicional de ensino superior, a renda anual aumenta em US$ 5.000.”

renda = (US$ 5.000 * anos_de_educação) + renda_base Esta abordagem é um exemplo de engenharia de solução (em vez de aprendizado de solução, como é o caso do método de regressão linear descrito abaixo).

Você poderia criar um modelo mais complexo incluindo algumas regras sobre tipo de diploma, anos de experiência profissional, níveis escolares, etc. Por exemplo: “Se o indivíduo concluiu o bacharelado ou um curso mais avançado, dê à estimativa de renda um multiplicador de 1,5x.”

Mas esse tipo de programação explícita baseada em regras não funciona bem com dados complexos. Imagine tentar projetar um algoritmo de classificação de imagens feito de declarações se-então que descrevem as combinações de brilho de pixel que deveriam ser rotuladas como “gato” ou “não gato”.

O aprendizado de máquina supervisionado resolve esse problema fazendo com que o computador faça o trabalho para você. Identificando padrões nos dados, a máquina é capaz de formar heurísticas. A principal diferença entre isso e o aprendizado humano é que o aprendizado de máquina funciona em hardware de computador e é melhor compreendido através das lentes da ciência da computação e da estatística, enquanto o casamento de padrões humano acontece em um cérebro biológico (enquanto realiza os mesmos objetivos).

No aprendizado supervisionado, a máquina tenta aprender a relação entre renda e educação do zero, executando dados de treinamento rotulados por meio de um algoritmo de aprendizado. Essa função aprendida pode ser usada para estimar a renda de pessoas cuja renda Y é desconhecida, desde que tenhamos como entrada os anos de escolaridade X. Em outras palavras, podemos aplicar nosso modelo aos dados de teste não rotulados para estimar Y.

O objetivo do aprendizado supervisionado é prever Y com a maior precisão possível ao receber novos exemplos nos quais X é conhecido e Y é desconhecido. A seguir exploraremos várias das abordagens mais comuns a isso.

As duas tarefas do aprendizado supervisionado: regressão e classificação

Regressão: prever um valor numérico contínuo. Por quanto será vendida esta casa? Classificação : atribuir um rótulo. Esta é a foto de um gato ou de um cachorro?

O restante desta seção se concentrará na regressão. Na Parte 2.2 nos aprofundaremos nos métodos de classificação.

Regressão: prever um valor contínuo

A regressão prevê uma variável-alvo contínua Y. Permite estimar um valor, como preços de habitação ou a expectativa de vida humana, com base nos dados de entrada X.

Aqui, variável-alvo significa a variável desconhecida que nos importamos de prever, e contínua significa que não há lacunas (descontinuidades) no valor que Y pode assumir. O peso e a altura de uma pessoa são valores contínuos. Variáveis ​​discretas, por outro lado, só podem assumir um número finito de valores: por exemplo, o número de filhos que alguém tem é uma variável discreta.

Prever a renda é um problema clássico de regressão. Seus dados de entrada X incluem todas as informações relevantes sobre os indivíduos no conjunto de dados que podem ser usadas ​​para prever a renda, como anos de educação, anos de experiência profissional, cargo ou CEP. Esses atributos são chamados de características, que podem ser numéricas (p. ex., anos de experiência profissional) ou categóricas (p. ex., cargo ou área de estudo).

Você desejará o máximo possível de observações de treinamento que relacionem essas características à saída-alvo Y, para que seu modelo possa aprender a relação f entre X e Y.

Os dados são divididos em um conjunto de dados de treinamento e um conjunto de dados de teste. O conjunto de treinamento possui rótulos, para que seu modelo possa aprender com esses exemplos rotulados. O conjunto de teste não possui rótulos, ou seja, ainda não se sabe o valor que se está tentando prever. É importante que seu modelo possa generalizar para situações nunca encontradas antes, para que possa ter um bom desempenho nos dados de teste.

Regressão Y = f(X) + ϵ , sendo X = (x1, x2…xn) Treinamento: a máquina aprende f a partir de dados de treinamento rotulados Teste: a máquina prevê Y a partir de dados de teste não rotulados Observe que X pode ser um tensor com qualquer número de dimensões. Um tensor 1D é um vetor (1 linha e muitas colunas), um tensor 2D é uma matriz (muitas linhas e muitas colunas) e então você pode ter tensores com 3, 4, 5 ou mais dimensões (p. ex., um tensor 3D com linhas, colunas e profundidade). Para uma revisão desses termos, consulte as primeiras páginas desta revisão de álgebra linear .

Em nosso exemplo 2D trivialmente simples, isso poderia assumir a forma de um arquivo .csv onde cada linha contém o nível de escolaridade e a renda de uma pessoa. Adicione mais colunas com mais características e você terá um modelo mais complexo, mas possivelmente mais preciso.

Então, como resolvemos esses problemas?

Como construímos modelos que fazem previsões precisas e úteis no mundo real? Fazemos isso usando algoritmos de aprendizado supervisionado.

Agora vamos para a parte divertida: conhecer os algoritmos. Exploraremos algumas das maneiras de abordar regressão e classificação e ilustraremos os principais conceitos de aprendizado de máquina durante o processo.

Regressão linear (mínimos quadrados ordinários)

“Trace a reta. Sim, isso conta como aprendizado de máquina.”

Primeiro, vamos nos concentrar em resolver o problema da previsão da renda com regressão linear, uma vez que modelos lineares não funcionam bem com tarefas de reconhecimento de imagem (esse é o domínio do aprendizado profundo, que exploraremos mais tarde).

Temos nosso conjunto de dados X e os valores-alvo correspondentes Y. O objetivo da regressão de mínimos quadrados ordinários (MQO) é aprender um modelo linear que podemos usar para prever um novo y dado um x não visto anteriormente com o mínimo de erro possível. Queremos adivinhar quanta renda alguém ganha com base em quantos anos de educação recebeu.

X_treinamento = [4, 5, 0, 2, …, 6] # anos de ensino superior Y_treinamento = [80, 91,5, 42, 55, …, 100] # renda anual correspondente, em milhares de dólares

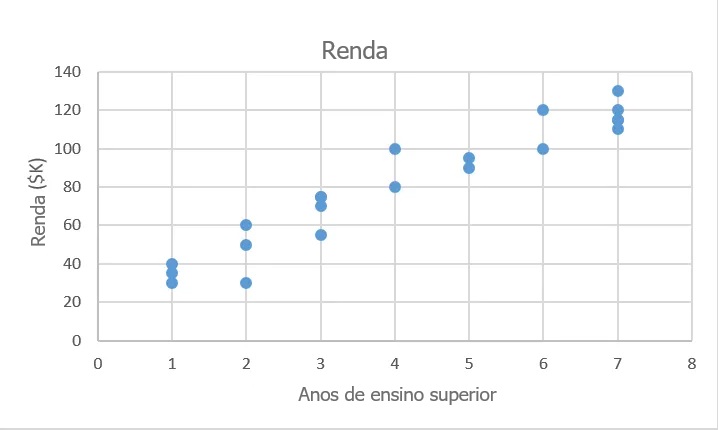
A regressão linear é um método paramétrico, o que significa que faz uma suposição sobre a forma da função que relaciona X e Y (abordaremos exemplos de métodos não paramétricos mais tarde). Nosso modelo será uma função que prevê ŷ dado um x específico:

β0 é a interseção y e β1 é a inclinação da nossa reta, ou seja, quanto a renda aumenta (ou diminui) com um ano a mais de educação.

Nosso objetivo é aprender os parâmetros do modelo (neste caso, β0 e β1) que minimizam o erro nas previsões do modelo.

Para encontrar os melhores parâmetros:

1. Defina uma função de custo, ou função de perda, que mede quão imprecisas são as previsões do nosso modelo.

2. Encontre os parâmetros que minimizem a perda, ou seja, que tornem o nosso modelo o mais preciso possível.

Graficamente, em duas dimensões, isso resulta numa reta de melhor ajuste. Em três dimensões, traçaríamos um plano e assim por diante com hiperplanos de dimensões superiores.

Uma observação sobre dimensionalidade: nosso exemplo é bidimensional para simplificar, mas normalmente você terá mais características (x’s) e coeficientes (betas) em seu modelo, p. ex., ao adicionar variáveis ​​mais relevantes para melhorar a precisão das previsões do seu modelo. Os mesmos princípios são generalizados para dimensões superiores, embora as coisas fiquem muito mais difíceis de visualizar além de três dimensões.

Matematicamente, observamos a diferença entre cada ponto de dados real (y) e a previsão do nosso modelo (ŷ). Eleve essas diferenças ao quadrado para evitar números negativos, penalize diferenças maiores, some-as e calcule a média em seguida. Essa é uma medida de quão bem nossos dados se ajustam à reta.

Para um problema simples como esse, podemos calcular uma solução fechada utilizando cálculo para encontrar os parâmetros beta ideais que minimizam a nossa função de perda. Mas conforme uma função de custo cresce em complexidade, não é mais viável encontrar uma solução fechada com cálculo. Essa é a motivação para uma abordagem iterativa chamada descida do gradiente, que nos permite minimizar uma função de perda complexa.

Descida do gradiente: aprenda os parâmetros

“Coloque uma venda, dê um passo ladeira abaixo. Você encontrou o fundo quando não tem para onde ir além de subir.”

A descida do gradidente sempre será mencionada, especialmente em redes neurais. Bibliotecas de aprendizado de máquina, como a scikit-learn e a TensorFlow, usam-na em segundo plano em todos os lugares; por isso vale a pena entender os detalhes.

O objetivo da descida do gradiente é encontrar o mínimo da função de perda do nosso modelo, obtendo iterativamente uma aproximação cada vez melhor dela.

Imagine-se caminhando por um vale com uma venda nos olhos. Seu objetivo é encontrar o fundo do vale. Como você faria?

Uma abordagem razoável seria tocar o solo ao seu redor e mover-se na direção em que o solo estiver mais inclinado. Dê um passo e repita o mesmo processo continuamente até que o solo esteja plano. Então, você sabe que chegou ao fundo de um vale; se você se mover para qualquer direção de onde está, terminará na mesma elevação ou mais acima.

Voltando à matemática, o solo torna-se a nossa função de perda, e a elevação no fundo do vale é o mínimo dessa função.

Vamos dar uma olhada na função de perda que vimos na regressão:

Vemos que isso é realmente uma função de duas variáveis: β0 e β1. Todas as demais variáveis ​​estão determinadas, já que X, Y e n são dados durante o treinamento. Queremos tentar minimizar essa função.

A função é f(β0,β1)=z. Para iniciar a descida do gradiente, você faz um palpite sobre os parâmetros β0 e β1 que minimizem a função.

A seguir, você encontra as derivadas parciais da função de perda em relação a cada parâmetro beta: [dz/dβ0, dz/dβ1]. Uma derivada parcial indica quanto a perda total aumenta ou diminui se você aumentar β0 ou β1 em uma quantidade muito pequena.

Em outras palavras, quanto aumentar a sua estimativa de renda anual, presumindo zero ensino superior (β0), aumentaria a perda (ou seja, imprecisão) do seu modelo? Você quer ir na direção oposta para acabar andando ladeira abaixo e minimizar a perda.

Da mesma forma, se você aumentar sua estimativa de quanto cada ano incremental de educação afeta a renda (β1), quanto isso aumenta a perda (z)? Se a derivada parcial dz/β1 for um número negativo, então aumentar β1 é bom porque reduzirá a perda total. Se for um número positivo, você deseja diminuir β1. Se for zero, não altere β1 porque isso significa que você atingiu o valor ideal.

Continue fazendo isso até chegar ao fundo, ou seja, até o algoritmo convergir e a perda ser minimizada. Existem muitos truques e casos excepcionais além do escopo desta série, mas geralmente é assim que você encontra os parâmetros ideais para seu modelo paramétrico .

Sobreajuste

Sobreajuste: “Sherlock, a sua explicação do que acabou de acontecer é muito específica para a situação.” Regularização: “Não complique as coisas, Sherlock. Vou dar um soco em você por cada palavra extra.” Hiperparâmetro (λ): “Aqui está a força com que vou socar você por cada palavra extra.”

Um problema comum no aprendizado de máquina é o sobreajuste: aprender uma função que explica perfeitamente os dados de treinamento com os quais o modelo aprendeu, mas não generaliza bem para dados de teste não vistos. O sobreajuste acontece quando um modelo aprende demais com os dados de treinamento a ponto de começar a captar idiossincrasias que não representam os padrões do mundo real. Isso se torna especialmente problemático conforme você torna seu modelo cada vez mais complexo. O subajuste é um problema relacionado em que seu modelo não é complexo o suficiente para capturar a tendência subjacente nos dados.

Conflito entre viés e variância Viés é a quantidade de erro introduzida quando aproximamos fenômenos do mundo real de um modelo simplificado. Variância é o quanto o erro de teste do seu modelo muda com base na variação nos dados de treinamento. Reflete a sensibilidade do modelo às idiossincrasias do conjunto de dados no qual foi treinado. Conforme um modelo aumenta em complexidade e tem mais balanço (flexibilidade), o seu viés diminui (ele explica bem os dados de treinamento), mas a variância aumenta (ele não generaliza tão bem). Em última análise, para ter um bom modelo, você precisa de um com baixo viés e baixa variância.

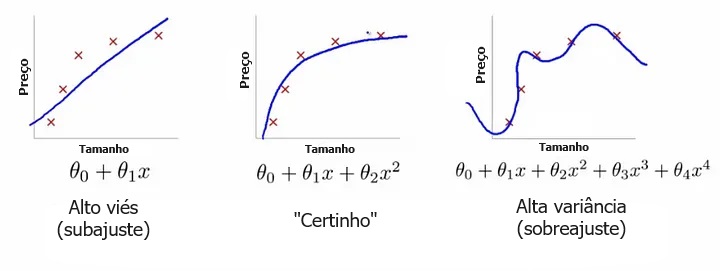
Lembre-se de que a única coisa que nos importa é o desempenho do modelo nos dados de teste. Você deseja prever quais e-mails serão marcados como spam antes de serem marcados, e não apenas construir um modelo que seja 100% preciso em reclassificar os e-mails que ele usou para construir a si mesmo. A visão é perfeita em retrospectiva; a verdadeira questão é se as lições aprendidas ajudarão no futuro.

O modelo à direita tem perda zero para os dados de treinamento porque se ajusta perfeitamente a cada ponto de dados. Mas a lição não se generaliza. Faria um péssimo trabalho ao tentar explicar um novo ponto de dados que ainda não esteja em jogo.

Duas maneiras de combater o sobreajuste:

1. Use mais dados de treinamento. Quanto mais você tiver, mais difícil será sobreajustar os dados, aprendendo demais com um único exemplo de treinamento.

2. Use regularização. Adicione uma penalidade na função de perda pela construção de um modelo que atribui muito poder explicativo a qualquer característica única ou permite que características demais sejam levadas em consideração.

A primeira parte da soma acima é a nossa função de custo normal. A segunda parte é um termo de regularização que adiciona uma penalidade para grandes coeficientes beta que dão muito poder explicativo a qualquer característica específica. Com esses dois elementos em vigor, a função de custo equilibra-se agora entre duas prioridades: explicar os dados de treinamento e evitar que essa explicação se torne demasiado específica.

O coeficiente lambda do termo de regularização na função de custo é um hiperparâmetro: uma configuração geral do seu modelo que pode ser aumentada ou diminuída (ou seja, ajustada) para melhorar o desempenho. Um valor lambda mais alto penalizará mais severamente grandes coeficientes beta que podem levar a um potencial sobreajuste. Para decidir o melhor valor de lambda, você usaria um método chamado validação cruzada, que envolve reter parte dos dados de treinamento durante o treinamento e, em seguida, ver quão bem o seu modelo explica a parte retida. Veremos isso com mais profundidade.

Uau! Conseguimos.

Aqui está o que abordamos nesta seção:

• Como o aprendizado de máquina supervisionado permite que os computadores aprendam com dados de treinamento rotulados sem serem explicitamente programados
• As tarefas do aprendizado supervisionado: regressão e classificação
• Regressão linear, um algoritmo paramétrico básico
• O aprendizado de parâmetros com a descida do gradiente
• Sobreajuste e regularização

Na próxima seção — Parte 2.2: Aprendizado Supervisionado II — falaremos sobre dois métodos fundamentais de classificação: regressão logística e máquinas de vetores de suporte.

Materiais práticos e leituras adicionais

2.1a: regressão linear

Para um tratamento mais completo da regressão linear, leia os capítulos 1–3 de An Introduction to Statistical Learning. O livro está disponível gratuitamente on-line e é um excelente recurso para compreender os conceitos de aprendizado de máquina, acompanhado de exercícios.

Para mais prática:

• Brinque com o conjunto de dados Boston Housing. Você pode usar software com boas interfaces gráficas, como Minitab e Excel, ou fazer isso da maneira mais difícil (mas mais gratificante) com Python ou R .
• Experimente um desafio Kaggle , p. ex., previsão de preços de habitação, e veja como outras pessoas abordaram o problema depois de tentar você mesmo.

2.1b: implementando a descida do gradiente

Para realmente implementar a descida do gradiente em Python, confira este tutorial. E aqui está uma descrição matematicamente mais rigorosa dos mesmos conceitos.

Na prática, você raramente precisará implementar a descida do gradiente do zero, mas entender como ela funciona nos bastidores permitirá que você a use de maneira mais eficaz e entenda por que as coisas quebram quando elas quebram.

---

Tradução: Luan Marques.

Link para o original.