Blog

De Nelson Elhage, Tristan Hume, Catherine Olsson, Nicholas Schiefer, Tom Henighan, Shauna Kravec, Zac Hatfield-Dodds, Robert Lasenby, Dawn Drain, Carol Chen, Roger Grosse, Sam McCandlish, Jared Kaplan, Dario Amodei, Martin Wattenberg, Christopher Olah

Seria muito conveniente se os neurônios individuais das redes neurais artificiais correspondessem a características claramente interpretáveis da entrada. Por exemplo, em um classificador “ideal” do ImageNet, cada neurônio dispararia apenas na presença de uma característica visual específica, como a cor vermelha, uma curva virada para a esquerda ou um focinho de cachorro. Empiricamente, em modelos que estudamos, alguns dos neurônios mapeiam claramente para características. Mas nem sempre é o caso que as características correspondem tão claramente aos neurônios, especialmente em grandes modelos de linguagem nos quais na verdade parece ser raro que os neurônios correspondam a características claras. Isso traz muitas questões. Por que é que às vezes os neurônios se alinham com características e às vezes não? Por que alguns modelos e tarefas têm muitos desses neurônios claros, enquanto são extremamente raros em outros?

Neste artigo, usamos modelos simplificados — pequenas redes de ReLU treinadas em dados sintéticos com características de entrada esparsas — para investigar como e quando os modelos representam mais características do que têm dimensões. Chamamos esse fenômeno de sobreposição [1, 2, 3]. Quando as características são esparsas, a sobreposição permite compressão além do que um modelo linear permitiria, às custas de “interferência” que requer filtragem não linear.

Considere um modelo simplificado no qual treinamos uma incorporação (embedding) de cinco características de importância variável¹ em duas dimensões, adicionamos um ReLU depois para filtragem e variamos a esparsidade das características. Com características densas, o modelo aprende a representar uma base ortogonal das duas características mais importantes (similar ao que a Análise de Componentes Principais poderia nos dar), e as outras três características não são representadas. Mas se tornamos as características esparsas, isso muda:

[imagem]

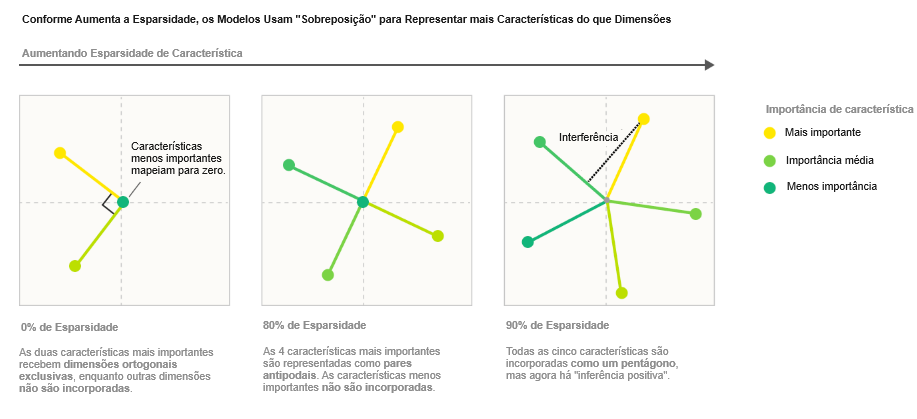
Não só os modelos podem armazenar características adicionais em sobreposição tolerando alguma interferência; também mostraremos que, pelo menos em certos casos limitados, os modelos podem realizar computação enquanto em sobreposição. (Em particular, mostraremos que os modelos podem colocar circuitos simples que calculam a função de valor absoluto em sobreposição.) Isso nos leva a propor que as redes neurais que observamos na prática estão de alguma forma simulando de forma ruidosa redes muito maiores e altamente esparsas. Em outras palavras, é possível que os modelos que treinamos possam ser considerados como fazendo “a mesma coisa que” um modelo imaginado muito maior, representando exatamente as mesmas características, mas sem interferência.

A sobreposição de características não é uma ideia nova. Vários artigos anteriores de interpretabilidade a consideraram [1, 2, 3, 4], e está muito relacionada ao tópico longamente estudado da amostragem compressiva na matemática [5], bem como às ideias de códigos distribuídos, densos e populacionais na neurociência [6] e aprendizado profundo [7]. Qual, então, é a contribuição deste artigo?

Para os pesquisadores de interpretabilidade, nossa principal contribuição é fornecer uma demonstração direta de que a sobreposição ocorre em redes neurais artificiais, dada uma configuração relativamente natural, sugerindo que isso também pode ocorrer na prática. Ou seja, mostramos um caso em que a interpretação de redes neurais como tendo uma estrutura esparsa em sobreposição não é apenas uma interpretação útil pós-hoc, mas na verdade a “verdade fundamental” de um modelo. Oferecemos uma teoria de quando e por que isso ocorre, revelando um diagrama de fases para a sobreposição. Isso explica por que os neurônios às vezes são “monossemânticos”, respondendo a uma única característica, e às vezes “polissemânticos” [8], respondendo a muitas características não relacionadas. Também descobrimos que, pelo menos em nosso modelo simplificado, a sobreposição exibe uma estrutura geométrica complexa.

Mas nossos resultados também podem ser de interesse mais amplo. Encontramos evidências preliminares de que a sobreposição pode estar ligada a exemplos adversários e compreensão (grokking), e também pode sugerir uma teoria para o desempenho de modelos de mistura de especialistas. Mais amplamente, o modelo simplificado que investigamos tem uma estrutura inesperadamente rica, exibindo mudanças de fase, uma estrutura geométrica baseada em politopos uniformes, saltos semelhantes a “níveis de energia” durante o treinamento e um fenômeno que é qualitativamente semelhante ao efeito Hall quântico fracionário na física, entre outros fenômenos marcantes. Investigamos originalmente o assunto para obter compreensão de neurônios claramente interpretáveis em modelos maiores, mas encontramos esses modelos simplificados surpreendentemente interessantes por si sós.

Resultados-chave dos nossos modelos de brinquedo Em nossos modelos simplificados, somos capazes de demonstrar que: – A sobreposição é um fenômeno real e observado. – Neurônios tanto monossemânticos quanto polissemânticos podem se formar. – Pelo menos alguns tipos de computação podem ser realizados em sobreposição. – Se as características são ou não armazenadas em sobreposição é governado por uma mudança de fase. – A sobreposição organiza características em estruturas geométricas como digonos, triângulos, pentágonos e tetraedros. Nossos modelos simplificados são redes de ReLU simples; então parece justo dizer que as redes neurais exibem essas propriedades em pelo menos alguns regimes, mas não está claro o que generalizar para redes reais.

Definição e motivação: características, direções e sobreposição

Em nosso trabalho, frequentemente pensamos em redes neurais como tendo características da entrada representadas como direções no espaço de ativações. Isso não é uma afirmação trivial. Não é óbvio que tipo de estrutura devemos esperar que as representações de redes neurais tenham. Quando dizemos algo como “as incorporações de palavras têm uma direção de gênero” ou “os modelos de visão têm neurônios detectores de curvas”, estamos implicitamente fazendo afirmações fortes sobre a estrutura das representações das redes.

Apesar disso, acreditamos que esse tipo de “hipótese de representação linear” é apoiado tanto por descobertas empíricas significativas quanto por argumentos teóricos. Pode-se pensar nisso como duas propriedades separadas, que exploraremos mais detalhadamente em breve:

1. Decomponibilidade: as representações das redes podem ser descritas em termos de características independentemente compreensíveis.
2. Linearidade: as características são representadas por direção.

Se esperamos fazer engenharia reversa em redes neurais, precisamos de uma propriedade como a decomponibilidade. A decomponibilidade é o que nos permite raciocinar sobre o modelo sem precisar entender o todo! Mas não basta as coisas serem decomponíveis: precisamos ser capazes de acessar a decomposição de alguma forma. Para fazer isso, precisamos identificar as características individuais dentro de uma representação. Em uma representação linear, isso corresponde a determinar quais direções no espaço de ativações correspondem a quais características independentes da entrada.

Às vezes, identificar direções de características é muito fácil porque as características parecem corresponder a neurônios. Por exemplo, muitos neurônios nas camadas iniciais do InceptionV1 claramente correspondem a características (p. ex., neurônios detectores de curvas). Por que é que às vezes obtemos essa propriedade extremamente útil, mas em outros casos não? Hipotetizamos que realmente existem duas forças contrárias impulsionando isso:

1. Base privilegiada: apenas algumas representações têm uma base privilegiada que incentiva as características a se alinharem com direções de base (ou seja, a corresponderem a neurônios).
2. Sobreposição: representações lineares podem representar mais características do que dimensões, usando uma estratégia que chamamos de sobreposição. Isso pode ser visto como redes neurais simulando redes maiores. Isso afasta as características da correspondência aos neurônios.

A sobreposição foi posta como hipótese em trabalhos anteriores [1, 2, 3, 4] e, em alguns casos, presumir algo como a sobreposição demonstrou ajudar a encontrar uma estrutura interpretável [1, 2]. No entanto, não estamos cientes de que a sobreposição de características tenha sido demonstrada de forma inequívoca em redes neurais antes ([10] demonstra um fenômeno relacionado da sobreposição de modelos). O objetivo deste artigo é mudar isso, demonstrando a sobreposição e explorando como ela interage com bases privilegiadas. Se a sobreposição ocorre em redes, ela influencia profundamente quais abordagens para pesquisa de interpretabilidade fazem sentido; então a demonstração inequívoca parece importante.

O objetivo desta seção será motivar essas ideias e desempacotá-las em detalhes.

Vale ressaltar que muitas das ideias desta seção têm conexões próximas com ideias em outras linhas de pesquisa de interpretabilidade (especialmente desentrelaçamento), neurociência (representações distribuídas, códigos populacionais, etc.), amostragem compressiva e muitas outras linhas de trabalho. Esta seção se concentrará em articular nossa perspectiva sobre o problema. […]

Fenômenos empíricos

Quando falamos sobre “características” e como elas são representadas, isso é essencialmente construção teórica em torno de vários fenômenos empíricos observados. Antes de descrevermos como conceituamos esses resultados, simplesmente descreveremos alguns dos principais resultados que motivam nosso pensamento:

• Incorporações de Palavras: um resultado famoso de Mikolov et al. [11] descobriu que as incorporações de palavras parecem ter direções que correspondem a propriedades semânticas, permitindo a incorporação de vetores aritméticos como
  • V("rei") - V("homem") + V("mulher") = V("rainha") (mas veja [12])
• Espaços Latentes: resultados semelhantes de “aritmética de vetores” e direções interpretáveis também foram encontrados para redes generativas adversárias (p. ex., [13]).
• Neurônios Interpretáveis: existe um corpo significativo de resultados encontrando neurônios que parecem ser interpretáveis (em redes neurais recorrentes [14, 15]; em redes neurais convolucionais [16, 17]; em redes generativas adversárias [18]), ativando-se em resposta a alguma propriedade compreensível. Este trabalho enfrentou algum ceticismo [19, 20]. Em resposta, vários artigos visaram fornecer explicações extremamente detalhadas de alguns neurônios específicos, na esperança de estabelecer exemplos de neurônios que realmente detectam alguma propriedade compreensível (notavelmente Cammarata et al. [9], mas também [21, 22]).
• Universalidade: muitos neurônios análogos que respondem às mesmas propriedades podem ser encontrados em redes [23, 3, 21].
• Neurônios Polissemânticos: ao mesmo tempo, também existem muitos neurônios que parecem não responder a uma propriedade interpretável da entrada, e em particular, muitos neurônios polissemânticos que parecem responder a misturas não relacionadas de entradas [8].

Como resultado, tendemos a pensar nas representações de redes neurais como sendo compostas por características que são representadas como direções. Vamos detalhar essa ideia nas seções seguintes.

O que são características?

Nosso uso do termo “característica” é motivado pelas propriedades interpretáveis da entrada às quais observamos neurônios (ou direções de incorporação de palavras) responderem. Existe uma rica variedade de tais propriedades observadas!² Gostaríamos de usar o termo “característica” para abranger todas essas propriedades.

No entanto, mesmo com essa motivação, acaba sendo bastante desafiador criar uma definição satisfatória de uma característica. Em vez de oferecer uma única definição na qual estejamos confiantes, consideramos três potenciais definições operacionais:

1. Características como funções arbitrárias. Uma abordagem seria definir características como qualquer função da entrada (como em [24]). Mas isso não parece se encaixar exatamente em nossas motivações. Há algo de especial sobre essas características que estamos observando: elas parecem, de alguma forma, ser abstrações fundamentais para raciocinar sobre os dados, com as mesmas características se formando de forma confiável em diferentes modelos. As características também parecem identificáveis: gato e carro são duas características, enquanto gato+carro e gato-carro parecem ser misturas de características em vez de características em algum sentido importante.
2. Características como propriedades interpretáveis. Todas as características que descrevemos são surpreendentemente compreensíveis para humanos. Poderíamos tentar usar isso para uma definição: características são a presença de “conceitos” compreensíveis para humanos na entrada. Mas parece importante permitir características que talvez não compreendamos. Se o AlphaFold descobrir alguma estrutura química importante para prever o enovelamento de proteínas, é bem possível que inicialmente não compreendamos!
3. Neurônios em Modelos Suficientemente Grandes. Uma abordagem final é definir características como propriedades da entrada para as quais uma rede neural suficientemente grande dedicará confiavelmente um neurônio para representar.³ Por exemplo, detectores de curvas parecem ocorrer de forma confiável em modelos de visão suficientemente sofisticados, e assim são uma característica. Para propriedades interpretáveis que atualmente só observamos em neurônios polissemânticos, a esperança é que um modelo suficientemente grande dedique um neurônio a elas. Essa definição é ligeiramente circular, mas evita os problemas das definições anteriores.

Escrevemos este artigo com a definição final “neurônios em modelos suficientemente grandes” em mente. No entanto, não estamos apegados demais a ela e, na verdade, achamos que é provavelmente importante não se apegar prematuramente a uma definição.⁴

Características como direções

Como mencionamos em seções anteriores, geralmente pensamos em características como sendo representadas por direções. Por exemplo, em incorporações de palavras, “gênero” e “realeza” parecem corresponder a direções, permitindo aritmética como

V("rei") - V("homem") + V("mulher") = V("rainha")[11]

Exemplos de neurônios interpretáveis também são casos de características como direções, já que quanto que um neurônio se ativa corresponde a uma direção de base na representação.

Vamos chamar uma representação de rede neural de linear se as características corresponderem a direções no espaço de ativações. Em uma representação linear, cada característica f_i tem uma direção de representação correspondente W_i. A presença de múltiplas características f₁, f₂ …, ativando-se com valores x_f1, x_f2… é representada por x_f1 W_f1 + x_f2 W_f2 … Para ficar claro, as características sendo representadas são quase certamente funções não lineares da entrada. É apenas o mapeamento de características para vetores de ativação que é linear. Note que se algo é uma representação linear depende do que você considera como as características.

Não achamos que seja coincidência que as redes neurais pareçam empiricamente ter representações lineares. Redes neurais são construídas a partir de funções lineares intercaladas com não linearidades. Em certo sentido, as funções lineares são a grande maioria da computação (por exemplo, conforme medido em FLOPs). Representações lineares são o formato natural para redes neurais representarem informações! Concretamente, existem três principais benefícios:

• Representações lineares são as saídas naturais de algoritmos óbvios que uma camada pode implementar. Se alguém configurar um neurônio para reconhecer uma determinada predefinição de peso, ele será ativado mais quando um estímulo corresponder melhor à predefinição e menos quando corresponder menos bem.
• Representações lineares tornam as características “linearmente acessíveis”. Uma camada típica de rede neural é uma função linear seguida de uma não linearidade. Se uma característica na camada anterior é representada linearmente, um neurônio na próxima camada pode “selecioná-la” e fazer com que ele se excite ou iniba consistentemente esse neurônio. Se uma característica fosse representada de forma não linear, o modelo não seria capaz de fazer isso em uma única etapa.
• Eficiência Estatística. Representar características como direções diferentes pode permitir generalizações não locais em modelos com transformações lineares (como os pesos das redes neurais), aumentando sua eficiência estatística com relação a modelos que só podem generalizar localmente. Esta visão é especialmente defendida em alguns dos escritos de Bengio (p. ex., [7]). Um argumento mais acessível pode ser encontrado neste post.

É possível construir representações não lineares e recuperar informações delas, se você usar várias camadas (embora mesmo esses exemplos possam ser vistos como representações lineares com características mais exóticas). […] No entanto, nossa intuição é que representações não lineares geralmente são ineficientes para redes neurais.

Alguém pode pensar que uma representação linear só pode armazenar tantas características quantas dimensões possui, mas acontece que esse não é o caso! Veremos que o fenômeno que chamamos de sobreposição permitirá que os modelos armazenem mais características — potencialmente muito mais características — em representações lineares.

[…]

Bases privilegiadas vs. não privilegiadas

Mesmo que as características sejam codificadas como direções, uma pergunta natural a fazer é: quais direções? Em alguns casos, parece útil considerar as direções de base, mas em outros não. Por que isso acontece?

Quando os pesquisadores estudam incorporações de palavras, não faz sentido analisar as direções de base. Não haveria motivo para esperar que uma dimensão de base fosse diferente de qualquer outra direção possível. Uma maneira de ver isso é imaginar a aplicação de alguma transformação linear aleatória M na incorporação de palavras, e aplicar M^-1 nos pesos seguintes. Isso produziria um modelo idêntico no qual as dimensões de base são completamente diferentes. Isso é o que queremos dizer com uma base não privilegiada. Claro, é possível estudar ativações sem uma base privilegiada: você só precisa identificar direções interessantes para estudar de alguma forma, como criar uma direção de gênero em uma incorporação de palavras tomando o vetor de diferença entre “homem” e “mulher”.

Mas muitas camadas de redes neurais não são assim. Muitas vezes, algo sobre a arquitetura torna as direções de base especiais, como a aplicação de uma função de ativação. Isso “quebra a simetria”, tornando essas direções especiais e potencialmente incentivando as características a se alinharem com as dimensões de base. Chamamos isso de base privilegiada e chamamos as direções de base de “neurônios”. Muitas vezes, esses neurônios correspondem a características interpretáveis.

[imagem]

Dessa perspectiva, só faz sentido perguntar se um neurônio é interpretável quando ele está em uma base privilegiada. Na verdade, geralmente reservamos a palavra “neurônio” para direções de base que estão em uma base privilegiada. (Veja uma discussão mais longa aqui).

Observe que ter uma base privilegiada não garante que as características estarão alinhadas com as bases — veremos que muitas vezes não estão! Mas é uma condição mínima para a pergunta sequer fazer sentido.

A hipótese da sobreposição

Mesmo quando há uma base privilegiada, muitas vezes acontece de os neurônios serem “polissemânticos”, respondendo a várias características não relacionadas. Uma explicação para isso é a hipótese da sobreposição [2, 1, 3]. Em termos gerais, a ideia da sobreposição é que as redes neurais “querem representar mais características do que têm neurônios”, e então elas exploram uma propriedade de espaços de alta dimensão para simular um modelo com muito mais neurônios.

[imagem]

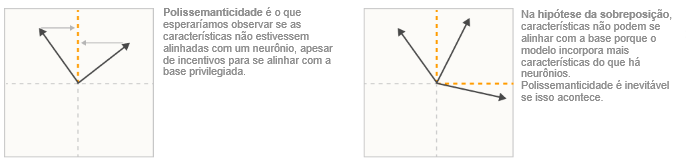
Vários resultados da matemática sugerem que algo assim possa ser plausível:

• Vetores Quase Ortogonais. Embora seja possível ter n vetores ortogonais em um espaço n-dimensional, é possível ter exp(n) muitos vetores “quase ortogonais” (< similaridade de cosseno ϵ) em espaços de alta dimensão. Veja o lema de Johnson-Lindenstrauss.
• Amostragem Compressiva. Em geral, se um vetor é projetado em um espaço de menor dimensão, não é possível reconstruir o vetor original. No entanto, isso muda se soubermos que o vetor original é esparso. Nesse caso, muitas vezes é possível recuperar o vetor original.

Concretamente, na hipótese da sobreposição, as características são representadas como direções quase ortogonais no espaço vetorial das saídas dos neurônios. Como as características são apenas quase ortogonais, a ativação de uma característica se parece com a ligeira ativação de outras características. Tolerar esse “ruído” ou “interferência” tem um custo. Mas para redes neurais com características altamente esparsas, esse custo pode ser compensado pelo benefício de poder representar mais características! (Crucialmente, a esparsidade reduz muito os custos, uma vez que características esparsas raramente estão ativas para interferir umas com as outras, e funções de ativação não lineares criam oportunidades para filtrar pequenas quantidades de ruído.)

[imagem]

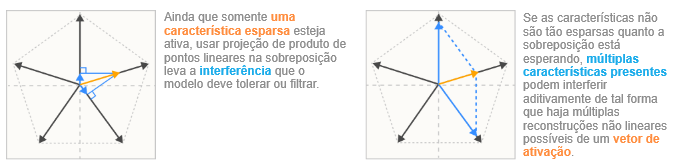
Uma maneira de pensar nisso é que uma pequena rede neural pode ser capaz de “simular” ruidosamente um modelo maior e esparsamente:

[imagem]

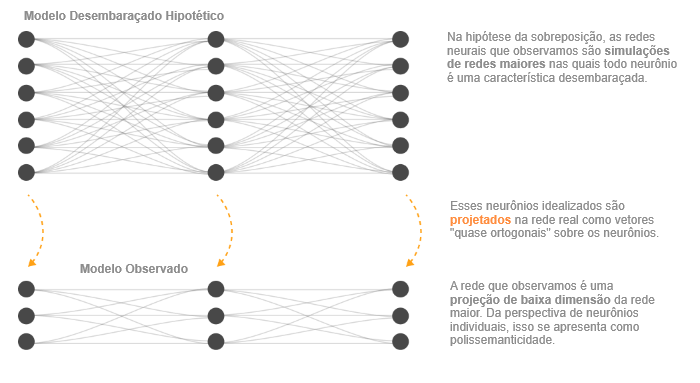
Embora tenhamos descrito a sobreposição com relação aos neurônios, ela também pode ocorrer em representações com uma base não privilegiada, como uma incorporação de palavras. Sobreposição simplesmente significa que há mais características do que dimensões.

Resumo: uma hierarquia de propriedades de características

As ideias desta seção podem ser concebidas em termos de quatro propriedades progressivamente mais rigorosas que as representações de redes neurais podem ter.

• Decomponibilidade: ativações de redes neurais que são decomponíveis podem ser decompostas em características, cujo significado não depende do valor de outras características. (Esta propriedade é, em última análise, a mais importante — veja o papel da decomposição em derrotar a maldição da dimensionalidade.)
• Linearidade: as características correspondem a direções. Cada característica f_i tem uma direção de representação correspondente W_i. A presença de múltiplas características f₁, f₂ … ativando-se com valores x_f1, x_f2… é representada por x_f1 W_f1 + x_f2 W_f2 …
• Sobreposição vs. Não Sobreposição: uma representação linear exibe sobreposição se W^TW não for invertível. Se W^TW for invertível, não exibe sobreposição.
• Alinhado à Base: uma representação está alinhada à base se todos os W_i forem vetores de base one-hot. Uma representação está parcialmente alinhada à base se todos os W_i forem esparsos. Isso requer uma base privilegiada.

As duas primeiras (decomponibilidade e linearidade) são propriedades que segundo nossa hipótese são amplamente difundidas, enquanto as últimas (não sobreposição e alinhado à base) são propriedades que acreditamos ocorrerem apenas às vezes.

Demonstrando a sobreposição

Se levarmos a hipótese da sobreposição a sério, uma primeira pergunta natural é se as redes neurais podem realmente representar de forma ruidosa mais características do que têm neurônios. Se não puderem, a hipótese da sobreposição pode ser confortavelmente descartada.

A intuição dos modelos lineares seria que isso não é possível: o melhor que um modelo linear pode fazer é armazenar os componentes principais. Mas veremos que adicionar apenas uma leve não linearidade pode fazer os modelos se comportarem de maneira radicalmente diferente! Essa será nossa primeira demonstração da sobreposição. (Também será uma lição objetiva sobre a complexidade mesmo de redes neurais muito simples.)

Configuração do experimento

Nosso objetivo é explorar se uma rede neural pode projetar um vetor de alta dimensão x ∈ Rⁿ num vetor de menor dimensão h ∈ R^m e então recuperá-lo.⁵

[imagem]

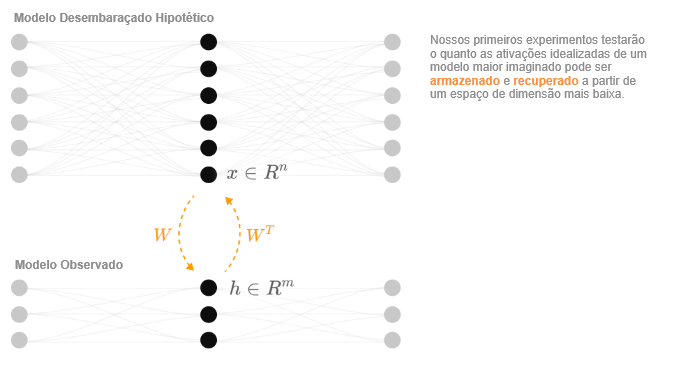
O vetor de características (X)

Começamos descrevendo o vetor de alta dimensão x: as ativações de nosso modelo idealizado e desembaraçado maior. Chamamos cada elemento x_i de “característica” porque estamos imaginando que as características estão perfeitamente alinhadas com os neurônios no modelo hipotético maior. Em um modelo de visão, isso pode ser um filtro de Gabor, um detector de curvas ou um detector de orelhas caídas. Em um modelo de linguagem, pode corresponder a um token que se refere a uma pessoa famosa específica ou a uma oração sendo um tipo particular de descrição.

Como não temos nenhuma verdade fundamental para as características, precisamos criar dados sintéticos para x que simulem quaisquer propriedades importantes que acreditamos que as características tenham do ponto de vista da modelagem delas. Fazemos três suposições principais:

• Esparsidade de Características: no mundo natural, muitas características parecem ser esparsas no sentido em que ocorrem apenas raramente. Por exemplo, na visão, a maioria das posições em uma imagem não contém uma borda horizontal, ou uma curva, ou uma cabeça de cachorro[3]. Na linguagem, a maioria dos tokens não se refere a Martin Luther King ou não faz parte de uma oração descrevendo música[3]. Essa ideia remonta ao trabalho clássico sobre visão e estatísticas de imagens naturais (veja, p. ex., Olshausen, 1997, a seção “Why Sparseness?”[26]). Por esse motivo, escolheremos uma distribuição esparsa para nossas características.
• Mais Características do que Neurônios: existe um número enorme de características potencialmente úteis que um modelo pode representar.⁶ O desequilíbrio entre características e neurônios em modelos reais parece ser uma tensão central nas representações de redes neurais.
• Características Variam em Importância: nem todas as características são igualmente úteis para uma tarefa específica. Algumas podem reduzir a perda mais do que outras. Para um modelo do ImageNet, no qual classificar diferentes espécies de cachorro é uma tarefa central, um detector de orelhas caídas pode ser uma das características mais importantes que ele pode ter. Em contraste, outra característica pode melhorar o desempenho apenas ligeiramente.⁷

Concretamente, nossos dados sintéticos são definidos da seguinte forma: os vetores de entrada x são dados sintéticos feitos para simular as propriedades que acreditamos que as verdadeiras características subjacentes de nossa tarefa têm. Consideramos cada dimensão x_i como uma “característica”. Cada uma tem uma esparsidade associada S_i e importância I_i. Deixamos x_i = 0 com probabilidade S_i, mas caso contrário, é distribuído uniformemente entre [0, 1].⁸ Na prática, focamos no caso em que todas as características têm a mesma esparsidade, S_i = S.

O modelo (X → X’)

Vamos, na verdade, considerar dois modelos, o que justificamos abaixo. O primeiro “modelo linear” é uma linha de base bem compreendida que não exibe sobreposição. O segundo “modelo de saída de ReLU” é um modelo muito simples que exibe sobreposição. Os dois modelos variam apenas na função de ativação final.

Modelo Linear	Modelo de Saída de ReLu
h = Wx	h = Wx
x′ = WTh + b	x′ = ReLU(WTh+b)
x′ = WTWx + b	x′ = ReLU(WTWx+b)

Por que esses modelos?

A hipótese da sobreposição sugere que cada característica no modelo de dimensão superior corresponde a uma direção no espaço de dimensão inferior. Isso significa que podemos representar a projeção para baixo como um mapeamento linear h = W_x. Note que cada coluna W_i corresponde à direção no espaço de dimensão inferior que representa uma característica x_i.

Para recuperar o vetor original, usaremos a transposição da mesma matriz W^T. Isso tem a vantagem de evitar qualquer ambiguidade sobre qual direção no espaço de dimensão inferior realmente corresponde a uma característica. Além disso, parece relativamente fundamentado em termos matemáticos ⁹ e funciona empiricamente.

Também adicionamos um viés. Uma motivação para isso é que permite ao modelo definir características que ele não representa para o seu valor esperado. Mas veremos mais tarde que a capacidade de definir um viés negativo é importante para a sobreposição por um segundo conjunto de razões: grosso modo, permite que os modelos descartem pequenas quantidades de ruído.

O último passo é se adicionar ou não uma função de ativação. Isso acaba sendo crucial para determinar se a sobreposição ocorre. Em uma rede neural real, quando as características são realmente usadas pelo modelo para fazer cálculos, haverá uma função de ativação; então parece razoável incluir uma no final.

A perda

Nossa perda é o erro médio quadrático ponderado pelas importâncias das características, I_i​, descritas acima:

[imagem]

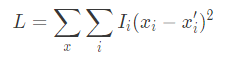
Resultados básicos

Nosso primeiro experimento será simplesmente treinar alguns modelos de saída de ReLU com diferentes níveis de esparsidade e visualizar os resultados. (Também treinaremos um modelo linear; se otimizado o suficiente, a solução do modelo linear não depende do nível de esparsidade.)

A principal questão é como visualizar os resultados. A maneira mais simples é visualizar W^TW (uma matriz de características por características) e b (um vetor de comprimento de característica). Note que as características são organizadas das mais importantes para as menos importantes; então os resultados têm uma estrutura bastante agradável. Aqui está um exemplo de como esse tipo de visualização pode ser, para um modelo pequeno (n = 20; m = 5;) que se comporta de forma “similar ao modelo linear esperado”, representando apenas tantas características quantas dimensões tem:

[imagem]

Mas o que realmente nos interessa é este fenômeno hipotético de sobreposição: o modelo representa “características extras” armazenando-as de forma não ortogonal? Existe uma maneira de abordar isso de forma mais explícita? Bem, uma questão é exatamente quantas características o modelo aprende a representar. Para qualquer característica, se ela é representada ou não é determinado por ||W_i||, a norma de seu vetor de incorporação.

Também gostaríamos de entender se uma determinada característica compartilha sua dimensão com outras características. Para isso, calculamos:

[imagem]

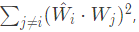
projetando todas as outras características no vetor de direção de W_i. Será 0 se a característica for ortogonal a outras características (azul escuro abaixo). Por outro lado, valores ≥ 1 significam que há algum grupo de outras características que podem ativar W_i tão fortemente quanto a própria característica i!

Podemos visualizar o modelo que examinamos anteriormente desta forma:

[imagem]

Agora que temos uma maneira de visualizar modelos, podemos começar a realmente fazer experimentos. Começaremos considerando modelos com apenas algumas características (n = 20; m = 5; I_i = 0,7ⁱ) ). Isso facilitará a visualizar o que acontece. Consideramos um modelo linear e vários modelos de saída de ReLU treinados em dados com diferentes níveis de esparsidade de características:

[imagem]

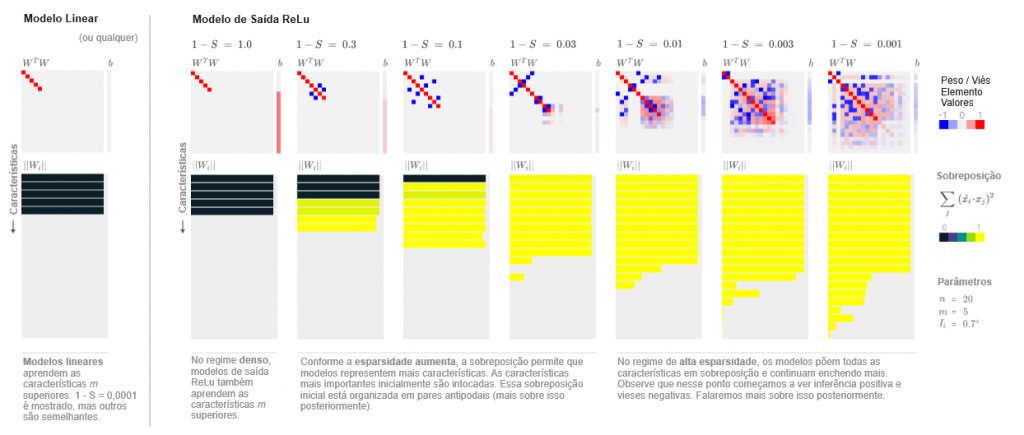
Como nossas intuições-padrão esperariam, o modelo linear sempre aprende as m características mais importantes, análogo a aprender os componentes principais. O modelo de saída de ReLU se comporta da mesma forma em características densas (1 – S = 1,0), mas conforme a esparsidade aumenta, vemos a sobreposição surgir. O modelo representa mais características ao fazê-las não serem ortogonais entre si. Ele começa com características menos importantes e gradualmente afeta as mais importantes. Inicialmente, isso envolve organizá-las em pares antipodais, sendo que o vetor de representação de uma característica é exatamente o negativo do outro, mas observamos que ela gradualmente transita para outras estruturas geométricas conforme representa mais características. […]

Os resultados são qualitativamente semelhantes para modelos com mais características e dimensões ocultas. Por exemplo, se considerarmos um modelo com m = 20 dimensões ocultas e n = 80 características (com importância aumentada para I_i = 0,9ⁱ) para dar conta de ter mais características), observamos essencialmente uma versão redimensionada da visualização acima:

[imagem]

Entendimento matemático

Na seção anterior, observamos um resultado empírico surpreendente: adicionar um ReLU à saída do nosso modelo permitiu uma solução radicalmente diferente — sobreposição — que não ocorre em modelos lineares.

O modelo no qual isso ocorre ainda é bastante matematicamente simples. Podemos entender analiticamente por que a sobreposição está ocorrendo? E, a propósito, por que adicionar uma única não linearidade faz as coisas serem tão diferentes do caso do modelo linear? Acontece que podemos obter uma resposta bastante satisfatória, revelando que nosso modelo é governado pelo equilíbrio de duas forças concorrentes — benefício de características e interferência — que serão uma intuição útil daqui para frente. Também descobriremos uma conexão com o famoso Problema de Thomson na química.

Vamos começar com o caso linear. Isso é bem entendido pelo trabalho anterior! Se alguém quiser entender por que os modelos lineares não exibem sobreposição, a resposta fácil é observar que os modelos lineares essencialmente realizam PCA. Mas isso não é totalmente satisfatório: se deixarmos de lado todo o nosso conhecimento e intuição sobre funções lineares por um momento, por que exatamente a superposição não pode ocorrer?

Um entendimento mais profundo pode vir dos resultados de Saxe et al. [28], que estudam a dinâmica de aprendizado de redes neurais lineares: ou seja, redes neurais sem funções de ativação. Tais modelos são, em última análise, funções lineares, mas porque são a composição de várias funções lineares, a dinâmica é potencialmente bastante complexa. A essência do artigo revela que os pesos da rede neural podem ser pensados como otimizando uma solução fechada simples. Podemos ajustar o problema deles para ser um pouco mais semelhante ao nosso caso linear,¹⁰ revelando a seguinte equação:

[imagem]

Os resultados de Saxe revelam que há fundamentalmente duas forças concorrentes que controlam a dinâmica de aprendizado no modelo considerado. Em primeiro lugar, o modelo pode alcançar uma perda melhor ao representar mais características (rotulamos isso de “benefício de características”). Mas também obtém uma perda pior se representar mais do que pode se encaixar ortogonalmente devido à “interferência” entre as características.¹¹ De fato, isso faz com que nunca valha a pena para o modelo linear representar mais características do que tem dimensões.¹²

Podemos alcançar um tipo semelhante de entendimento para o modelo de saída de ReLU? Concretamente, gostaríamos de entender:

[imagem]

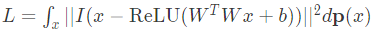
sendo que x é distribuído de tal forma que x_i = 0 com probabilidade S.

A integral sobre x se decompõe em um termo para cada padrão de esparsidade de acordo com a expansão binomial de ((1 – S) + S)ⁿ. Podemos agrupar os termos de esparsidade juntos, reescrevendo a perda como:

[imagem]

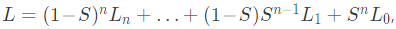
com cada L_k correspondendo à perda quando a entrada é um vetor k-esparso. Note que quando S → 1, L₁ e L₀ dominam. O termo L₀, correspondente à perda em um vetor zero, é apenas uma penalidade para vieses positivos, ∑_i​ReLU(b_i​)². Portanto, o termo interessante é L₁, a perda em vetores 1-esparsos:

[imagem]

Essa nova equação é vagamente similar ao famoso Problema de Thomson na química. Em particular, se presumirmos uma importância uniforme e que há um número fixo de características com ||W_i||=1 e o restante tem ||W_i||=0, e que b_i = 0, então o termo do benefício de características é constante e o termo de interferência se torna um Problema de Thomson generalizado: estamos apenas carregando pontos na superfície da esfera com uma função de energia ligeiramente incomum. […]

Outra propriedade interessante é que o ReLU torna a interferência negativa livre no caso 1-esparso. Isso explica por que as soluções que vimos preferem ter apenas interferência negativa quando possível. Além disso, usar um viés negativo pode converter pequenas interferências positivas essencialmente em interferências negativas.

E quanto aos termos correspondentes a vetores menos esparsos? Deixamos que o leitor os escreva explicitamente, mas a ideia principal é que existem múltiplas interferências compostas, e as “características ativas” podem experimentar interferência. Em uma seção posterior, veremos que as características muitas vezes se organizam em grafos de interferência esparsos de forma que apenas um pequeno número de características interfira em outra característica; é interessante notar que isso reduz a probabilidade de interferência composta e torna o termo de perda 1-esparso mais importante com relação aos outros.

[…]

Notas

1. Sendo que “importância” é um multiplicador escalar na perda de erro quadrática média.

2. No contexto da visão, isso variou de neurônios de baixo nível, como detectores de curvas [9] e detectores de alta-baixa frequência [21], a neurônios mais complexos, como detectores de cabeças de cachorro orientadas ou detectores de carros [3], a neurônios extremamente abstratos correspondentes a pessoas famosas, emoções, regiões geográficas e muito mais [22]. Nos modelos de linguagem, os pesquisadores encontraram direções de incorporações de palavras, como uma direção macho-fêmea ou singular-plural [11], neurônios de baixo nível que desambiguam palavras que ocorrem em vários idiomas, neurônios muito mais abstratos e neurônios de saída de “ação” que ajudam a produzir determinadas palavras [4].

3. Essa definição é mais complicada do que parece. Especificamente, algo é uma característica se houver um tamanho de modelo grande o suficiente para que ele receba um neurônio dedicado. Isso cria uma definição do tipo “epsilon-delta”. Nosso entendimento atual — como veremos em seções posteriores — é que modelos arbitrariamente grandes ainda podem ter uma grande fração de seus recursos em sobreposição. Entretanto, para qualquer característica específica, supondo que a curva de importância da característica não seja plana, ela deve receber um neurônio dedicado. Essa definição pode ser útil para dizer que algo é uma característica — detectores de curvas são uma característica porque você os encontra em uma gama de modelos maiores do que um tamanho mínimo –, mas não é útil para a definição muito mais comum de neurônio dedicado.

4. Um famoso livro de Lakatos [25] ilustra a importância da incerteza sobre as definições e como é importante repensar as definições no contexto da pesquisa.

5. A configuração desse experimento também pode ser vista como um autocodificador que reconstrói x.

6. Um modelo de visão com generalidade suficiente pode se beneficiar da representação de todas as espécies de plantas e animais e de todos os objetos manufaturados que ele potencialmente vê. Um modelo de linguagem pode se beneficiar da representação de cada pessoa que já foi mencionada por escrito. Essas são apenas as primeiras impressões sobre as características plausíveis, mas já parecem ser mais do que qualquer modelo tem neurônios. Na verdade, os modelos de linguagem de grande porte comprovadamente sabem sobre pessoas de destaque muito modesto — presumivelmente, mais pessoas do que eles têm neurônios. Isso é um argumento comum na discussão sobre a plausibilidade dos “neurônios-avôs” na neurociência, mas parece ainda mais forte para as redes neurais artificiais.

7. Por motivos computacionais, não vamos nos concentrar nisso neste artigo, mas muitas vezes imaginamos um número infinito de características com importância assintoticamente próxima de zero.

8. A escolha de ter características distribuídos uniformemente é arbitrária. Uma distribuição exponencial ou de lei de potência também seria muito natural.

9. Lembre-se de que W^T =W^-1 se W for ortonormal. Embora W não possa ser literalmente ortonormal, nossa intuição a partir da amostragem compressiva é que ele será “quase ortonormal” no sentido de Candes & Tao [27].

10. Fazemos com que o modelo seja x′=W^TWx, mas deixamos x distribuído de forma gaussiana como em Saxe.

11. Como um breve aparte, é interessante contrastar a interferência do modelo linear, ∑_i≠j​∣Wi​⋅WJ​∣², com a noção de coerência na amostragem compressiva, max_i≠j∣Wi​⋅WJ​∣. Podemos vê-los como as normas L² e L^∞ do mesmo vetor.

12. Para provar que a sobreposição nunca é ótima em um modelo linear, resolva para que o gradiente da perda seja zero ou consulte Saxe et al.

Referências

Consulte as referências no documento original.

---

Tradução: Luan Marques

Link para o original