De Guillaume Alain e Yoshua Bengio

Resumo

Os modelos de redes neurais têm a reputação de serem caixas-pretas. Propomos monitorar as características em cada camada de um modelo e medir quão adequadas são para a classificação. Usamos classificadores lineares, que chamamos de “sondas”, treinados inteiramente de forma independente do próprio modelo.

Isso nos ajuda a entender melhor os papéis e a dinâmica das camadas intermediárias. Demonstramos como isso pode ser usado para desenvolver uma melhor intuição sobre os modelos e para diagnosticar problemas potenciais.

Aplicamos essa técnica aos modelos populares Inception v3 e Resnet-50. Entre outras coisas, observamos experimentalmente que a separabilidade linear das características aumenta monotonicamente ao longo da profundidade do modelo.

1. Introdução

A história recente das redes neurais profundas apresenta um número impressionante de novos métodos e melhorias tecnológicas para permitir o treinamento de redes mais profundas e poderosas. As redes neurais profundas ainda carregam parte de sua reputação original de serem caixas-pretas, mas têm sido feitos muitos esforços para entender melhor o que elas fazem, qual é o papel de cada camada (Yosinski et al., 2014), como podemos interpretá-las (Zeiler e Fergus, 2014) e como podemos enganá-las (Biggio et al., 2013; Szegedy et al., 2013).

Neste artigo, consideramos as características de cada camada separadamente e equipamos um classificador linear para prever as classes originais. Referimo-nos a esses classificadores lineares como “sondas” e garantimos que nunca influenciamos o modelo em si ao realizar medições com as sondas. Sugerimos que o leitor pense nessas sondas como termômetros usados para medir a temperatura simultaneamente em muitos locais diferentes. De forma mais ampla, o cerne da ideia é que existem quantidades interessantes que podemos relatar com base nas características de muitas camadas independentes se permitirmos que os “instrumentos de medição” tenham seus próprios parâmetros treináveis (desde que não influenciem o modelo em si).

No contexto deste artigo, estamos trabalhando com redes neurais convolucionais em tarefas de classificação de imagens nos conjuntos de dados MNIST e ImageNet (Russakovsky et al., 2015). Naturalmente, equipamos sondas classificadoras lineares para prever essas classes, mas, em geral, é possível monitorar o desempenho das características em qualquer outro objetivo.

Nossas contribuições neste artigo são duplas.

Em primeiro lugar, introduzimos essas “sondas” como uma ferramenta geral para entender redes neurais profundas. Mostramos como elas podem ser usadas para caracterizar diferentes camadas, depurar modelos ruins ou ter uma ideia de como o treinamento está progredindo em um modelo bem comportado. Embora nossa ideia proposta compartilhe semelhanças com Montavon et al. (2011), nossa análise é muito diferente.

Em segundo lugar, observamos que as medições das sondas são surpreendentemente monotônicas, o que significa que o grau de separabilidade linear das características das camadas aumenta à medida que alcançamos as camadas mais profundas. O nível de regularidade com que isso acontece é surpreendente, considerando que isso não é tecnicamente parte do objetivo de treinamento. Isso ajuda a entender a dinâmica das redes neurais profundas.

[…]

3. Monitorando com sondas

3.1. Teoria da informação e melhoramentos monotônicos à separabilidade linear

A motivação inicial para as sondas classificadoras lineares estava relacionada a uma reflexão sobre a natureza da informação (no sentido de entropia da palavra) que passa de uma camada para a próxima.

Nova informação nunca é adicionada à medida que avançamos em um modelo. Se considerarmos o problema típico da classificação de imagens, a representação dos dados é transformada ao longo de várias camadas, para ser finalmente usada por um classificador linear na última camada.

No caso de um classificador binário (digamos, que detecta a presença ou ausência de um leão em uma imagem da savana como na Figura 1), poderíamos dizer que havia no máximo um bit de informação a ser descoberto na imagem original. Leão ou não leão? Aqui não estamos interessados em medir a informação sobre os pixels de uma imagem que queremos reconstruir. Isso seria um problema diferente.

Isso é ilustrado de forma formal pela Desigualdade de Processamento de Dados. Ela afirma que, para um conjunto de três variáveis aleatórias que satisfazem a dependência

X → Y → Z

então temos que

I(X;Z) ≤ I(X; Y)

sendo que I(X, Y) é a informação mútua.

Figura 1: O despejo hexadecimal representado acima tem mais conteúdos informacionais do que a imagem abaixo. Apenas uma delas pode ser processada pelo cérebro humano a tempo de salvar vidas. A conveniência computacional importa, não apenas a entropia.

A tarefa de um classificador de redes neurais profundas é criar uma representação para a camada final que possa ser facilmente alimentada a um classificador linear (ou seja, a forma mais elementar de classificador útil). A perda de entropia cruzada aplica muita pressão diretamente na última camada para torná-la linearmente separável. Qualquer grau de separabilidade linear nas camadas intermediárias acontece apenas como um subproduto.

Por um lado, temos que cada camada tem menos informações do que sua camada genitora. Por outro lado, observamos experimentalmente na Seção 3.5, 4.1 e 4.2 que características de camadas mais profundas funcionam melhor com classificadores lineares para prever os rótulos-alvo. À primeira vista, isso pode parecer uma contradição.

Uma das lições importantes é que redes neurais realmente se tratam de destilar representações computacionalmente úteis, e não de conteúdos de informação conforme descritos pelo campo da Teoria da Informação.

3.2. Sondas classificadoras lineares

Considere o cenário comum em aprendizado profundo no qual estamos tentando classificar os dados de entrada X para produzir uma distribuição de saída sobre D classes. A última camada do modelo é um mapa densamente conectado para D valores seguido por um softmax, e treinamos minimizando a entropia cruzada.

Em cada camada, podemos pegar as características H_k dessa camada e tentar prever os rótulos corretos y usando um classificador linear parametrizado como

sendo que H_k ∈ H são as características da camada oculta k, [0, 1]^D é o espaço de distribuições categóricas das D classes-alvo, e (W, b) são os pesos e vieses das sondas a serem aprendidos de forma a minimizar a perda usual de entropia cruzada.

Seja L_k^train a perda empírica desse classificador linear f_k avaliado no conjunto de treinamento. Também podemos definir L_k^valid e L_k^test exportando o mesmo classificador linear nos conjuntos de validação e teste.

Sem fazer nenhuma suposição sobre o próprio modelo em treinamento, podemos ainda assim pressupor que esses f_k são, eles próprios, otimizados de modo que, em qualquer dado momento, eles reflitam a coisa atualmente ótima que pode ser feita com as características presentes.

Referimo-nos a esses classificadores lineares como “sondas” na tentativa de esclarecer nosso pensamento sobre o modelo. Essas sondas não afetam o treinamento do modelo. Elas apenas medem o nível de separabilidade linear das características em uma determinada camada. O bloqueio da retropropagação das sondas para o próprio modelo pode ser alcançado usando tf.stop_gradient no Tensorflow (ou seu equivalente em Theano), ou gerenciando os parâmetros da sonda separadamente dos parâmetros do modelo.

Observe que podemos evitar o problema dos mínimos locais porque treinar um classificador linear usando entropia cruzada de softmax é um problema convexo.

Neste artigo, estudamos

• como L_k diminui à medida que k aumenta (veja a Seção 3.1),
• a utilidade de L_k como uma ferramenta de diagnóstico (veja a Seção 5.1).

3.3. Preocupação prática: L_k^train vs. L_k^valid

A razão pela qual nos importamos com a otimidade das sondas na Seção 3.2 é porque ela abstrai o problema de otimizá-las. Quando uma função geral g(x) tem um mínimo global único, podemos falar sobre esse mínimo sem ambiguidade, mesmo que, na prática, provavelmente vamos usar apenas uma aproximação conveniente do mínimo.

Isso é aceitável em um contexto onde buscamos uma melhor intuição sobre modelos de aprendizado profundo usando sondas classificadoras lineares. Se um pesquisador julgar que as medições são úteis para aprofundar sua compreensão do modelo (e agir com base nessa intuição), então ele não deve se preocupar muito com quão próximo está da otimidade.

Isso também se aplica à questão sobre se devemos priorizar L_k^train ou L_k^valid. Argumentaríamos que L_k^valid parece ser uma quantidade mais significativa para monitorar, mas, dependendo de nossa configuração experimental, pode não ser fácil rastrear L_k^valid em todas as circunstâncias.

Além disso, para os propósitos de muitos dos experimentos neste artigo, escolhemos relatar o erro de classificação em vez da entropia cruzada, já que ela é, em última instância, frequentemente a quantidade que mais importa. Relatar o erro de classificação top5 também poderia ter sido possível.

3.4. Preocupação prática: redução de dimensão sobre características

Outro problema prático pode surgir quando certas camadas de uma rede neural têm uma quantidade excessivamente grande de características. As primeiras camadas do Inception v3, por exemplo, têm alguns milhões de características quando multiplicamos altura, largura e canais. Isso leva a parâmetros para uma única sonda que ocupa vários gigabytes de armazenamento, o que é desproporcionalmente grande quando consideramos que o conjunto inteiro de parâmetros do modelo ocupa menos espaço do que isso.

Nesses casos, temos três sugestões possíveis para reduzir o espaço de características no qual equipamos as sondas.

• Utilize apenas um subconjunto aleatório das características (mas sempre as mesmas). Isso é utilizado no modelo Inception v3 na Seção 4.2.
• Projete as características para um espaço de menor dimensão. Aprenda esse mapeamento. Isso provavelmente é uma ideia pior do que parece, pois a matriz de projeção em si pode ocupar muito espaço de armazenamento (ainda mais do que os parâmetros da sonda).
• Ao lidar com características na forma de imagens (altura, largura, canais), podemos realizar uma partilha 2D ao longo da (altura, largura) de cada canal. Isso reduz o número de características ao número de canais. Isso é utilizado no modelo ResNet-50 na Seção 4.1.

Na prática, ao usar sondas classificadoras lineares em qualquer modelo sério (ou seja, não MNIST), temos que escolher uma maneira de reduzir o número de características utilizadas.

Observe que também queremos evitar uma situação em que nossas sondas estejam simplesmente sobreajustando sobre as características porque há muitas características. Foi demonstrado recentemente que modelos muito grandes podem colocar rótulos aleatórios no ImageNet (Zhang et al., 2016). Esta é uma situação que queremos evitar porque as medições das sondas seriam completamente sem sentido nessa situação. A redução da dimensionalidade ajuda com essa preocupação.

3.5. Exemplo básico no MNIST

Nesta seção, executamos o modelo convolucional MNIST fornecido pelo tensorflow/models do repositório github (imagem/mnist/convolutional.py). Selecionamos esse modelo para reprodução e para demonstrar como examinar facilmente modelos populares usando sondas.

Começamos esboçando o modelo na Figura 2. Relatamos os resultados no início e no final do treinamento na Figura 3. Uma das dinâmicas interessantes a serem observadas é quão úteis são as primeiras camadas, apesar do fato de o modelo estar completamente não treinado. Projeções aleatórias podem ser úteis para classificar dados, e isso tem sido estudado por outros (Jarrett et al., 2009).

Figura 2: Este modelo gráfico representa a rede neural que vamos usar para o MNIST. O modelo poderia ser escrito de forma mais compacta, mas o representamos desta forma para expor todas as localizações onde vamos inserir sondas. O próprio modelo é simplesmente composto por duas camadas convolucionais seguidas por duas camadas totalmente conectadas (sendo uma o classificador final). No entanto, inserimos sondas em cada lado de cada convolução, função de ativação e função de partilha. Isso é um pouco excessivo, mas o tamanho pequeno do modelo torna isso relativamente fácil de fazer.

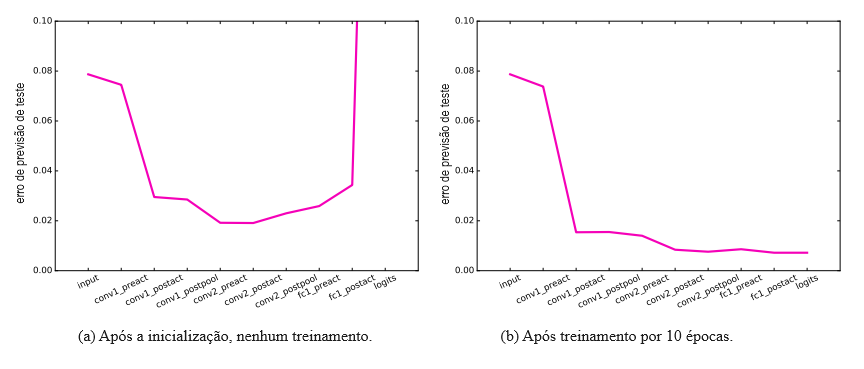
Figura 3: Representamos aqui o erro de previsão do teste para cada sonda, no início e no final do treinamento. Esta medição foi obtida através da interrupção precoce com base em um conjunto de validação de 104 elementos. As sondas são impedidas de sobreajustar os dados de treinamento. Podemos ver que, no início do treinamento (à esquerda), as camadas inicializadas aleatoriamente ainda estavam fornecendo transformações úteis. O erro de previsão do teste passa de 8% para 2% apenas usando essas características aleatórias. O maior impacto vem do primeiro ReLU. No final do treinamento (à direita), o erro de previsão do teste está melhorando em cada camada (com exceção de um pequeno solavanco em fc1_preact).

3.6. Outros objetivos

Note que seria inteiramente possível usar sondas classificadoras lineares em um conjunto diferente de rótulos. Pelo mesmo motivo que é possível transferir muitas camadas de uma tarefa de visão para outra (p. ex., com classes diferentes), não estamos limitados a equipar sondas usando o mesmo domínio.

Inserir sondas em muitas camadas diferentes de um modelo é essencialmente uma maneira de fazer a seguinte pergunta:

Existe alguma informação sobre o fator _______ presente nesta parte do modelo?

[…]

Referências

[Consulte as referências do artigo original.]

---

Tradução: Luan Marques

Link para o original