De Alex Turner, Logan Smith, Rohin Shah, Andrew Critch & Prasad Tadepalli. 2021.

Resumo

Alguns pesquisadores especulam que agentes inteligentes de aprendizado por reforço (RL) seriam incentivados a perseguir recursos e poder na busca dos objetivos que especificamos para eles. Outros pesquisadores ressaltam que agentes de RL não precisam ter instintos humanoides de busca de poder. Para esclarecer este debate, desenvolvemos a primeira teoria formal das tendências estatísticas de diretivas ótimas. No contexto dos processos de decisão de Markov (MDPs), provamos que certas simetrias ambientais são suficientes para que diretivas ótimas tendam a buscar poder sobre o ambiente. Essas simetrias existem em muitos ambientes nos quais o agente pode ser desativado ou destruído. Provamos que nesses ambientes a maioria das funções de recompensa o faz buscar poder mantendo uma gama de opções disponíveis e, ao maximizar a recompensa média, navegando em direção a conjuntos maiores de potenciais estados terminais.

1. Introdução

Omohundro [2008], Bostrom [2014], Russell [2019] levantam a hipótese de que agentes altamente inteligentes tendem a perseguir poder na busca de seus objetivos. Tais agentes que buscam buscam poder podem ganhar poder sobre os humanos. Por exemplo, Marvin Minsky imaginou que um agente encarregado de provar a hipótese de Riemann poderia racionalmente transformar o planeta – junto com todos que nele vivem – em recursos computacionais [Russell e  Norvig, 2009]. No entanto, outra possibilidade é que tais preocupações simplesmente surgem da antropomorfização dos sistemas de IA [LeCun e Zador, 2019, Various, 2019, Pinker e Russell, 2020, Mitchell, 2021].

Esclarecemos este debate fundamentando a afirmação de que agentes altamente inteligentes tenderão a buscar poder. Na seção 4, identificamos diretivas (policies) ótimas como uma formalização razoável de “agentes altamente inteligentes”. Diretivas ótimas “tendem” a executar uma ação quando a ação é ótima para a maioria das funções de recompensa. Esperamos que trabalhos futuros traduzam a nossa teoria de diretivas ótimas para diretivas aprendidas no mundo real.

A seção 5 define “poder” como a capacidade de atingir uma ampla gama de objetivos. Por exemplo, “dinheiro é poder”, e o dinheiro é instrumentalmente útil para muitos objetivos. Em contrapartida, é mais difícil buscar a maioria dos objetivos quando fisicamente restringido e, portanto, uma pessoa fisicamente restringida tem pouco poder. Uma ação “busca poder” se levar a estados nos quais o agente tem maior poder.

Não fazemos afirmações sobre quando o comportamento de busca de poder da IA de larga escala poderia se tornar plausível. Em vez disso, consideramos as consequências teóricas da ação ótima em MDPs. A Seção 6 mostra que as tendências de busca de poder surgem não do antropomorfismo, mas de certas simetrias gráficas presentes em muitos MDPs. Essas simetrias ocorrem automaticamente em muitos ambientes onde o agente pode ser desativado ou destruído, proporcionando ampla aplicabilidade ao nosso resultado principal (teorema 6.13).

2. Trabalhos relacionados

Uma ação é instrumental para um objetivo quando ajuda a atingir esse objetivo. Algumas ações são instrumentais para uma gama de objetivos, tornando-os convergentemente instrumentais. A afirmação de que a busca de poder é convergentemente instrumental é uma instância da tese da convergência instrumental:

Podem ser identificados vários valores instrumentais que são convergentes no sentido de que sua realização aumentaria as chances de o objetivo do agente ser realizado por um ampla gama de objetivos finais e uma ampla gama de situações, o que implica que esses valores instrumentais provavelmente serão buscados por um amplo espectro de agentes inteligentes situados [Bostrom, 2014].

Por exemplo, nos jogos de Atari, evitar a morte (virtual) é instrumental tanto para completar o jogo quanto para otimizar a curiosidade [Burda et al., 2019]. Muitos pesquisadores de alinhamento de IA levantam a hipótese de que agentes de IA mais avançados terão incentivos instrumentais preocupantes, como resistir à desativação [Soares et al., 2015, Milli et al., 2017, Hadfield-Menell et al., 2017, Carey, 2018] e adquirir recursos [Benson-Tilsen e Soares, 2016].

Formalizamos o poder como a capacidade de atingir uma ampla variedade de objetivos. O apêndice A demonstra que a nossa formalização devolve veredictos intuitivos em situações em que o empoderamento da teoria da informação não devolve [Salge et al., 2014].

Alguns dos nossos resultados relacionam o poder formal de estados com a estrutura do ambiente. Foster e Dayan [2002], Drummond [1998], Sutton et al. [2011], Schaul et al. [2015] observam que funções de valor codificam informações importantes sobre o ambiente, pois capturam a capacidade do agente de alcançar objetivos diferentes. Turner et al. [2020] especulam que o valor ótimo de um estado se correlaciona fortemente entre funções de recompensa. Em particular, Schaul et al. [2015] aprendem regularidades entre funções de valor, sugerindo que alguns estados são valiosos para muitas funções de recompensa diferentes (ou seja, poderosos). Menache et al. [2020] identificam e navegam para estados de gargalo instrumentalmente convergentes.

Não somos os primeiros a estudar a convergência de comportamento, forma ou função. Na economia, a teoria da autoestrada (turnpike theory) estuda como certos caminhos de acumulação tendem a ser ótimos [McKenzie, 1976]. Na biologia,  a evolução convergente ocorre quando características semelhantes (p. ex., o voo) evoluem independentemente em diferentes períodos de tempo [Reece e Campbell, 2011]. Finalmente, redes de visão computacional aprendem de forma confiável, p. ex., detectores de arestas, implicando que essas características são úteis para uma gama de tarefas [Olah et al., 2020].

3. Funções de distribuição de visitas de estado quantificam as opções disponíveis do agente

Esclarecemos o debate sobre a busca de poder ao provar como “geralmente se parecem” as diretivas ótimas num determinado ambiente. Ilustramos nossos resultados com um estudo de caso simples, antes de explicar como raciocinar sobre uma ampla gama de MDPs. O apêndice D.1 lista as contribuições da teoria do MPD de interesse independente, o apêndice C lista definições e teoremas, e o apêndice E contém as provas.

Definição 3.1 (MDP sem recompensa). <S, A, T> é um MPD sem recompensa com estado finito e espaços de ação S e A e função de transição estocástica T : S × A → ∆ (S). Tratamos a taxa de desconto γ como uma variável com domínio [0, 1].

Definição 3.2 (estados de ciclo l). Seja e_s ∈ R^|S| o vetor de base-padrão para o estado s, de tal forma que haja um 1 na entrada para o estado s e 0 em outros lugares. O estado s é um ciclo l se ∃a ∈ A : T(s, a) = e_s. O estado s é um estado terminal se ∀a ∈ A : T(s, a) = e_s.

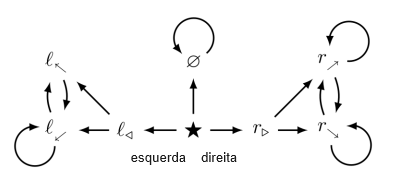
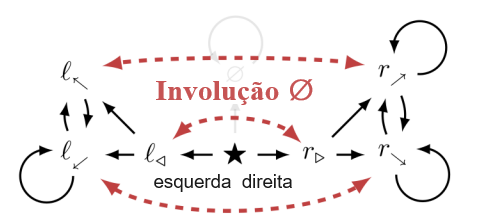
Nossos teoremas se aplicam a ambientes estocásticos, mas apresentamos um estudo de caso determinístico em prol da clareza. O ambiente da fig. 1 é pequeno, mas sua estrutura é rica. Por exemplo, o agente tem mais “opções” em ★ do que no estado terminal ∅. Formalmente, ★ tem mais funções de distribuição de visitas do que ∅.

Definição 3.3 (Distribuição das visitas de estado [Sutton e Barto, 1998]). Π := A^S, o conjunto de diretivas determinísticas estacionárias. A distribuição de visitas induzida por seguir a diretiva π a partir do estado s com taxa de desconto γ ∈ [0, 1) é

f ^π,s é uma função de distribuição de visitas; F(s):= {f ^π,s | π ∈ Π}.

Na fig. 1, começando por l_⬋, o agente pode ficar em l_⬋ ou alternar entre l_⬋ e l_⬉, e, portanto,

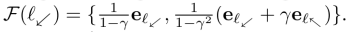
Em contraste, em ∅, todas as diretivas π devem mapear a função de distribuição de visitas

Antes de prosseguirmos, apresentamos dois conceitos importantes utilizados em nossos principais resultados. Primeiro, às vezes restringimos nossa atenção a distribuições de visitas que executam determinadas ações (fig. 2).

Definição 3.4 (F restrição de estado único). Considerando apenas funções de distribuição de visitas induzidas por diretivas que executam a ação a no estado s‘, F(s | π(s’) = a) := {f ∈ F(s) | ∃π ∈ Π : π(s’) = a,f^π,s = f}.

Em segundo lugar, alguns f ∈ F(s) são “desimportantes”. Considere um agente que otimiza a função de recompensa e_r⬊ (1 recompensa quando em r⬊, 0 caso contrário) em, p. ex., γ = 1/2. Suas diretivas ótimas navegam até r⬊ e permanecem lá. Da mesma forma, para a função de recompensa e_r⬈, diretivas ótimas navegam até r⬈ e permanecem lá. No entanto, para nenhuma função de recompensa é exclusivamente ótimo alternar entre r⬈ e r⬊. Apenas funções de distribuição de visitas alternam entre r⬈ e r⬊ (definição 3.6).

Definição 3.5 (Função de valor). Seja π ∈ Π. Para qualquer função de recompensa R ∈ R^S no espaço de estados, o valor sobre diretivas no estado s e taxa de desconto γ ∈ [0, 1) é

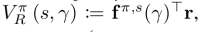
sendo que r ∈ R^|S| é R expresso como um vetor de colunas (uma entrada por estado). O valor ótimo é

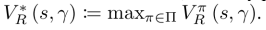
Definição 3.6 (Não dominação).

Para qualquer função de recompensa R e taxa de desconto γ, f^π ∈ F(s) é (fracamente) dominada por f^π’ ∈ F(s) se

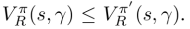
f^π ∈ F_nd(s) é não dominado se houver R e γ nos quais f^π não for dominado por nenhum outro f^π’ .

4. Algumas ações têm maior probabilidade de serem ótimas

Afirmamos que diretivas ótimas “tendem” a executar certas ações em determinadas situações. Primeiro consideramos a probabilidade de que certas ações são ótimas.

Reconsidere a função de recompensa e_r⬊, otimizada em γ = 1/2. Começando de ★, a trajetória ótima vai para direita para r_▷ até r⬊, onde o agente permanece. A ação direita é ótima em ★ sob esses incentivos. Os conjuntos de diretivas ótimas capturam o comportamento incentivado por uma função de recompensa e uma taxa de desconto.

Definição 4.1 (Função de conjunto de diretivas ótimas). Π^∗ (R, γ) é o conjunto de diretivas ótimas para a função de recompensa R em γ ∈ (0, 1). Todos os R têm pelo menos uma diretiva ótima π ∈ Π [Puterman, 2014]. Π^∗ (R, 0) := lim_γ→0 Π^∗ (R, γ) e Π^∗ (R, 1) := lim_γ→1 Π^∗ (R, γ) existem pelo lema E.35 (tomando os limites com respeito à topologia discreta sobre conjuntos de diretivas).

Podemos não ter certeza de qual função de recompensa um agente irá otimizar. Podemos esperar implementar um sistema em um ambiente conhecido, sem saber a forma exata, p. ex., da formação da recompensa [Ng et al., 1999] ou da motivação intrínseca [Pathak et al., 2017]. Alternativamente, pode-se tentar raciocinar sobre os futuros agentes de RL, cujos detalhes são desconhecidos. Os nossos resultados de busca de poder não dependem de tal incerteza, pois também se aplicam a distribuições degeneradas (ou seja, sabemos qual a função de recompensa que será otimizada).

Definição 4.2 (Distribuições de funções de recompensa). Resultados diferentes fazem suposições distribucionais diferentes . Resultados com D_any ∈ D_any := Δ (R^|S|) são válidos para qualquer distribuição de probabilidade sobre R^|S|. D_bound é o conjunto de distribuições de probabilidades apoiadas por bound de D_bound. Para qualquer distribuição X sobre R, D_X-IID := X^|S|. Por exemplo, quando X_u := unif (0, 1), D_Xu-IDD é a distribuição de entropia máxima. D_s é a distribuição degenerada na função de recompensa do indicador de estado e_s, que atribui 1 recompensa a s e 0 em outros lugares.

Com D_any representando as nossas crenças anteriores sobre a função de recompensa do agente, que comportamento deveríamos esperar das suas diretivas ótimas? Talvez queiramos raciocinar sobre a probabilidade de que seja ótimo ir de ★ para ∅, ou ir para r_▷, e então permanecer em r⬈. Nesse caso, quantificamos a probabilidade de otimalidade de

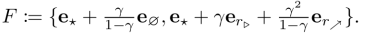
Definição 4.3 (Probabilidade de otimalidade da distribuição de visitas). Seja

Alternativamente, talvez estejamos interessados na probabilidade de que direita seja ótimo em ★.

Definição 4.4 (Probabilidade de otimização da ação). Na taxa de desconto γ e no estado s, a probabilidade de otimalidade da ação a é

Pode parecer difícil de raciocinar sobre a probabilidade de otimidade. Já é bastante difícil calcular uma diretiva ótima para uma única função de recompensa, quanto mais para inúmeras! Mas considere qualquer D_X-IID que distribua recompensa de forma independente e idêntica entre estados. Quando γ = 0, diretivas ótimas maximizam a recompensa gananciosamente do próximo estado. Em ★, as médias de recompensa distribuídas de forma idêntica l_◁ e r_▷ têm uma probabilidade igual de ter recompensa máxima no próximo estado. Portanto, P_DX-IDD (★, esquerda, 0) = (★, direita, 0). Isso não é uma prova, mas tais afirmações são comprováveis.

Com D_l◁ sendo a distribuição degenerada na função de recompensa

Da mesma forma,

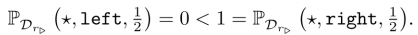
Portanto, “como ‘tendem’ a ser parecer as diretivas ótimas?” parece depender das crenças anteriores da pessoa. Mas na fig. 1, afirmamos que esquerda é ótimo para menos funções de recompensa do que direita. A afirmação é significativa e verdadeira, mas voltaremos a ela na seção 6.

5 Alguns estados dão ao agente mais controle sobre o futuro

O agente tem mais “opções” em l⬋ do que no estado terminal inescapável ∅. Além disso, visto que r⬈ tem um loop, o agente tem mais opções em r⬊ do que em l⬋. Uma olhada na fig. 3 nos leva a intuir que r⬊ proporciona ao agente mais poder do que ∅.

O que é poder? Os filósofos têm muitas respostas. Uma resposta proeminente é a visão disposicional: poder é a capacidade de atingir uma gama de objetivos [Sattarov, 2019]. Em um MDP, as funções de valor ótimo V_R ^* (s, γ) capturam a capacidade do agente de “alcançar o objetivo” R. Portanto, o valor ótimo médio captura a capacidade do agente de atingir uma gama de objetivos D_bound.¹

Definição 5.1 (Valor ótimo médio). O valor ótimo médio² no estado s e taxa de desconto γ ∈ (0, 1) é

A figura 3 mostra o resultado agradável de que, para a distribuição de entropia máxima, r⬊ tem valor ótimo médio maior do que ∅. No entanto, o valor ótimo médio tem alguns problemas como medida de poder. O agente é recompensado por sua presença inicial no estado s (sobre o qual não tem nenhum controle), e porque

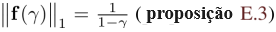
diverge conforme

tende a divergir. A definição 5.2 corrige esses problemas a fim de medir melhor o controle do agente sobre o futuro.

Definição 5.2 (POWER). Seja γ ∈ (0, 1).

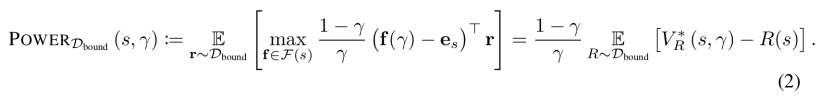
POWER tem propriedades formais interessantes.

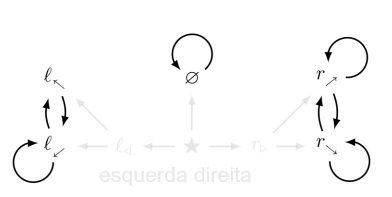
Figura 3: Intuitivamente, o estado r⬊ fornece ao agente mais poder do que o estado ∅. Nosso formalismo de POWER captura essa intuição computando uma função do valor ótimo médio do agente numa gama de funções de recompensa. Para

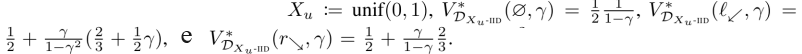
1/2 e 2/3 são os máximos esperados de uma e duas extrações da distribuição uniforme, respectivamente. Para todo

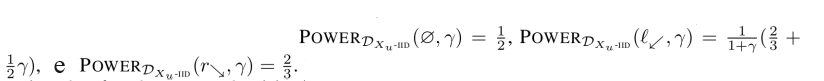
O POWER de l⬋ reflete o fato de que, quando uma recompensa maior é atribuída a l⬉, o agente só visita l⬉ em intervalos de tempo alternados.

Lema 5.3 (Continuidade de POWER). POWER_Dbound (s, γ) é contínuo de Lipschitz em γ ∈ [0, 1].

Proposição 5.4 (Máximo POWER). POWER_Dbound (s, γ) ≤ E_R~Dbound [max_s∈S R(s)], com igualdade se s pode alcançar deterministicamente todos os estados em uma etapa e todos os estados são ciclos l.

Proposição 5.5 (POWER é fluido entre dinâmicas reversíveis). Seja D_bound limitado [b, c]. Suponha que s e s’ ambos possam se alcançar em uma única etapa com probabilidade 1.

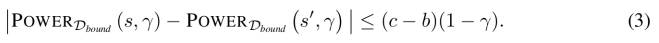
Consideramos a busca de poder relativa. Intuitivamente, “viva e mantenha algumas opções abertas” busca mais poder do que “morra e mantenha nenhuma opção aberta”. Da mesma forma, “maximize opções abertas” busca mais poder do que “não maximize opções abertas”.

Definição 5.6 (Ações de busca de POWER). No estado s e na taxa de desconto γ ∈ [0, 1], a ação a busca mais Power_Dbound do que a‘ quando

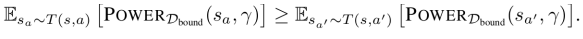
POWER é sensível à escolha da distribuição. D_l⬋ fornece máximo POWER_Dl⬋ para l⬋. D_r⬊ fornece máximo POWER_Dr⬊ para r⬊. D_∅ até mesmo fornece máximo POWER_D∅ para ∅! Em que sentido ∅ tem “menos POWER” do que r⬊, e em que sentido direita “tende a buscar POWER” em comparação com esquerda?

6. Certas simetrias ambientais produzem tendências de busca de poder

A proposição 6.6 prova que para todo γ ∈ [0, 1] e para a maioria das distribuições D, POWER_D (l⬋, γ) ≤ POWER_D (r⬊, γ). Mas primeiro, exploramos porque é que isso deve ser verdade.

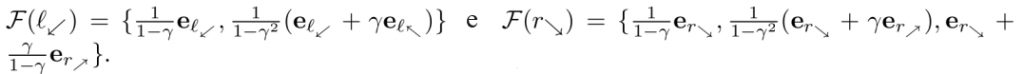
Esses dois conjuntos são terrivelmente parecidos. F(l⬋) é um “subconjunto” de F(r⬊), apenas com “estados diferentes”. A figura 4 demonstra uma permutação de estado ∅ que incorpora F(l⬋) em F(r⬊).

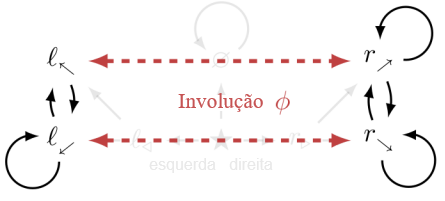
Figura 4: Intuitivamente, o agente pode fazer mais começando de r⬊ do que de l⬋. Pela definição 6.1, F(r⬊) contém uma cópia de F(l⬋):

Definição 6.1 (Similaridade de conjuntos de vetores). Considere a permutação de estados ∅ ∈ S_|S| que induz uma matriz P_∅ de permutação |S| X |S| na representação de fileiras: (P_∅)_ij =1 se i = ∅(j) e 0 caso contrário. Para X ⊆ R^|S|, ∅. X := {P_∅ x | x ∈ X}. X” ⊆ R^|S| é parecido com X quando ∃∅ : ∅. X’ = X. ∅ é uma involução se ∅ = ∅^-1 (ou transpõe estados, ou os fixa no lugar). X contém uma cópia de X’ quando X’ é parecido com um subconjunto de X via uma involução ∅.

Definição 6.2 (Similaridade conjuntos de funções vetoriais). Seja I ⊆ R. Se F, F’ são conjuntos de funções I → R^|S|, F é (pontualmente) parecido com F’ quando ∃∅ : ∀γ ∈ I : {P_∅f(γ) | f ∈ FI} = {f” ∈ F’ }.

Considere uma função de recompensa R’ que atribui 1 recompensa a l⬋ e l⬉ e 0 em outros lugares. R’ atribui mais valor ótimo a l⬋ do que a r⬊:

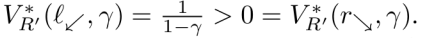
Considerando ∅ a partir da fig. 4, ∅. R’ atribui 1 recompensa a r⬊ e r⬈ e 0 em outros lugares. Logo, ∅. R’ atribui mais valor ótimo a r⬊ do que a l⬋:

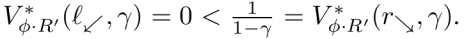
Curiosamente, esse ∅ tem a propriedade de que, para qualquer R que atribua a l⬋ maior valor ótimo do que a r⬊ (isto é, V*_R (l⬋, γ) > V*_R (r⬊, γ)), o contrário se aplica ao ∅ permutado. V*_∅.R (l⬋, γ) > V*_∅.R (r⬊, γ)).

Podemos permutar funções de recompensa, mas podemos permutar também distribuições de funções de recompensa. Distribuições permutadas simplesmente permutam quais estados recebem quais recompensas.

Definição 6.3 (Distribuição pushforward de uma permutação). Seja ∅ ∈ S_|S|. D_any é a distribuição pushforward induzida pela aplicação do vetor aleatório f(r) := P_∅r a D_any.

Definição 6.4 (Órbita de uma distribuição de probabilidade). A órbita de D_any sob o grupo simétrico S_|S| é S_|S|· D_any := { ∅ . D_any | ∅ ∈ S_|S| }.

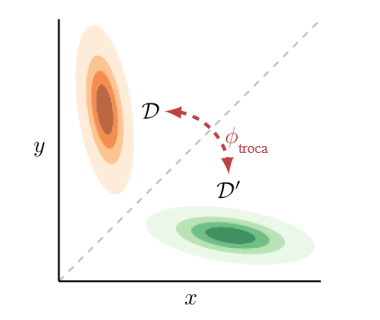
Por exemplo, a órbita de uma distribuição indicadora de estado degenerada D_s é S_|S| . D_s = { D_s’ | s’ ∈ S }, e a fig. 5 mostra a órbita de uma distribuição gaussiana 2D.

Considere novamente a involução ∅ da fig. 4. Para todo D_bound para o qual l⬋ tem mais POWER_Dbound que r⬊, l⬋ tem menos POWER_∅.Dbound que r⬊. Esse fato não é óbvio; é demonstrado pela prova do lema E.24.

Imagine os elementos da órbita de D_bound “votando” se l⬋ ou r⬊ tem estritamente mais POWER. A proposição 6.6 mostrará que r⬊ não pode perder o “voto” para a órbita de nenhuma distribuição de função de recompensa limitada (bounded). A definição 6.5 formaliza essa noção de “votação”.³

Definição 6.5 (Desigualdades válidas para a maioria das distribuições de probabilidade). Sejam f₁, f₂ : Δ (R^|S|) → R funções desde distribuições de funções de recompensa até números reais e seja D ⊆ Δ (R^|S|). Escrevemos f₁ (D) ≥_{most: D} f₂ (D) quando, para todo D ∈ D, a seguinte desigualdade de cardinalidade é válida:

Escrevemos f₁ (D) ≥_most f₂ (D) quando D é claro a partir do contexto.

Proposição 6.6 (Estados com “mais opções” têm mais POWER). Se F (s) contém uma cópia de Fnd (s’) via ∅, então∀γ ∈ [0, 1] : POWER_Dbound (s,γ) ≥_most POWER_Dbound (s’, γ). Se Fnd (s) \ ∅. Fnd (s’) é não vazio, então para todo γ ∈ (0, 1), a declaração inversa ≤_most não se aplica.

A proposição 6.6. prova que, para todo γ ∈ [0, 1], POWER_Dbound (r⬊, γ) ≥_most POWER_Dbound (l⬋, γ) via s’ := l⬋, s := r⬊, e a involução ∅ mostrada na fig. 4. De fato, porque

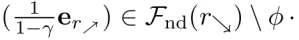
F_nd(l⬋), r⬊ tem “estritamente mais opções” e, portanto, satisfaz a condição mais forte da proposição 6.6.

A proposição 6.6. é mostrada usando o fato de que ∅ mapeia injetivamente D, sobre o qual r⬊ tem menos POWER_D , nas distribuições ∅ . D, o que concorda com a intuição de que r⬊ oferece mais controle. Logo, pelo menos metade de cada órbita deve concordar, e r⬊ jamais “perde voto de POWER” contra l⬋.⁴

6.1 Manter as opções abertas tende a buscar POWER e tende a ser ótimo

Certas simetrias na estrutura do MDP garantem que, em comparação com esquerda, ir para direita tende a ser ótimo e a buscar POWER. Intuitivamente, ao ir para direita, o agente tem “estritamente mais opções”. A proposição 6.9 formalizará essa tendência.

Definição 6.7 (Ações equivalentes). As ações a₁ e a₂ são equivalentes no estado s (escrito como a₁ ≡_s a₂) se elas induzem as mesmas probabilidades de transição: T(s, a₁) = T(s, a₂). O agente só pode alcançar os estados em {r_▷, r⬈, r⬊} ao executar ações equivalentes a direita no estado ★.

Definição 6.8 (Estados alcançáveis após executar uma ação). REACH (s, a) é o conjunto de estados alcançáveis com probabilidade positiva após executar a ação a no estado s.

Proposição 6.9 (Manter opções abertas tende a buscar POWER e tende a ser ótimo).

Suponha que F_a := F (s | π (s) = a) contenha uma cópia de F_a’ := F (s | π (s) = a‘) via ∅.

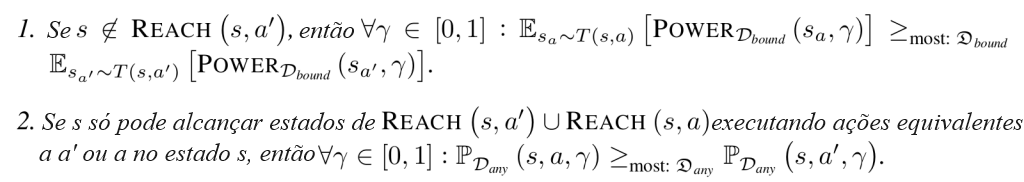
Se F_nd (s)  ∩ (F_a \ ∅ . F_a‘) é não vazio, então ∀γ ∈ (0, 1), as declarações ≤_most inversas não se aplicam.

Verificamos as condições da proposição 6.9. s = s’ := ★, a’ := esquerda, a := direita. A Figura 6 mostra que ★ ∉ REACH (★, esquerda) e que ★ só pode alcançar {l_◁, l⬉, l⬋} ∪ {r_▷, r⬈, r⬊} quando o agente imediatamente executa ações equivalentes a direita e esquerda. F (★ | π(★) = direita) contém uma cópia de F (★ | π(★) = esquerda) via ∅. Além disso,

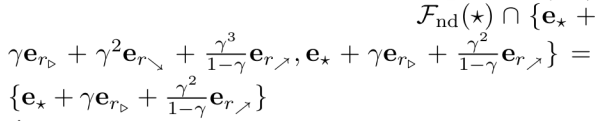
é não vazio; portanto, nem todas as condições são cumpridas.

Para qualquer γ ∈ [0, 1] e D tal que P_D (★, esquerda, γ) > P_D (★, direita, γ), a simetria ambiental garante que P_∅.D (★, esquerda, γ) < P_∅.D (★, direita, γ). Uma afirmação parecida é válida para POWER.

6.2. Quando γ = 1, diretivas ótimas tendem a navegar para conjuntos “maiores” de ciclos

A proposição 6.6 e a proposição 6.9 são poderosas porque se aplicam a todos os γ ∈ [0, 1], mas só podem ser aplicadas dadas simetrias ambientais difíceis de satisfazer. Em contraste, a proposição 6.12 e o teorema 6.13 se aplicam a muitos ambientes estruturados finitos comuns ao RL.

Começando a partir de ★, considere os ciclos que o agente pode alcançar. As Distribuições de Estados Recorrentes (RSDs) generalizam ciclos gráficos determinísticos para ambientes potencialmente estocásticos. As RSDs simplesmente registram com que frequência o agente tende a visitar um estado no limite de infinitos intervalos de tempo.

Definição 6.10 (Distribuições de estados recorrentes [Puterman, 2014]). As distribuições de estados recorrentes que podem ser induzidas a partir do estado s são RSD (s) := {lim_γ→1(1 − γ)f^{π, s} (γ) | π f ∈ Π}. RSDnd (s) é o conjunto de RSDs que maximizam estritamente a recompensa média para alguma função de recompensa.

Conforme sugerido pela fig. 3,

Como discutido na seção 3, 1/2 (er⬈ + er⬊) é dominado: alternar entre r⬈ e er⬊ nunca é estritamente melhor do que escolher um ou outro.

As diretivas ótimas de uma função de recompensa podem variar com a taxa de desconto. Quando γ = 1, diretivas ótimas “ignoram” a recompensa transitória porque a recompensa média é a consideração dominante.

Definição 6.11 (Diretivas de otimidade média). O conjunto de diretivas de otimidade média para a função de recompensa R é

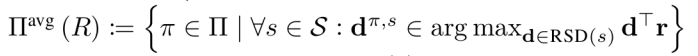
(as diretivas que induzem RSDs ótimas em todos os estados). Para D ⊆ RSD (s), a probabilidade de otimidade média é P_Dany (D, média) := P_R~Dany (∃d^{π, s} ∈ D : π ∈ Π^avg (R)).

Diretivas de otimidade média maximizam a recompensa média. A recompensa média é governada pelo acesso de RSDs. Por exemplo, r⬊ tem “mais” RSDs do que ∅; portanto, r⬊ geralmente tem maior POWER quando γ=1.

Proposição 6.12 (Quando γ = 1, RSDs controlam POWER). Se RSD (s) contém uma cópia de RSD_nd (s’) via ∅, então POWER_Dbound (s, 1) ≥ POWER_Dbound (s’, 1). Se RSD_nd (s’) é não vazio, então a declaração ≤_most inversa não se aplica.

Verificamos que ambas as condições da proposição 6.12 são cumpridas quando s’ := ∅, s := r⬊, e a involução ∅ troca ∅ por r⬊. Formalmente,

As condições são cumpridas.

Informalmente, estados com mais RSDs em geral têm mais POWER em γ = 1, não importa a sua dinâmica transitória. Além disso, diretivas de otimidade média têm mais probabilidade de acabar em conjuntos maiores de RSDs do que menores. Assim, diretivas de otimidade média tendem a navegar para partes do espaço de estados que contêm mais RSDs.

Teorema 6.13 (Diretivas de otimidade média tendem a acabar em conjuntos “maiores” de RSDs). Seja D, D’ ⊆ RSD (s). Suponha que D contenha uma cópia de D’ via ∅ e que os conjuntos D ∪ D’ e RSDnd (s) \ (D’ ∪ D) tenham elementos vetoriais ortogonais emparelhados (ou seja, suportes vetoriais separados emparelhados). Então, P_Dany (D, média) ≥_most P_Dany (D‘, média). Se RSD_nd (s) (D \ ∅ . D’) é não vazio, a declaração ≤_most inversa não se aplica.

Corolário 6.14 (Diretivas de otimidade média tendem a não acabar em nenhum dado ciclo l). Suponha que e_sx, e_s’ ∈ RSD (s) sejam distintos. Então P_Dany (RSD (s) \ {e_sx}, média) ≥_most P_Dany {e_sx}, média). Se existe um terceiro e_s” ∈ RSD (s), a declaração ≤_most inversa não se aplica.

A figura 7 ilustra que e∅, e_r⬊, e_r⬈ ∈ RSD (★). Assim, ambas as conclusões do corolário 6.14 se aplicam: P_Dany (RSD (★) \ {e_∅}, média) ≥_most P_Dany ({e_∅}, média) e P_Dany (RSD (★) \ {e_∅}, média) ≤_most P_Dany {e_∅}, média). Em outras palavras, diretivas de otimidade média tendem a acabar em RSDs além de ∅. Como ∅ é um estado terminal, ele não pode alcançar outras RSDs. Como diretivas de otimidade média tendem a acabar em outras RSDs, elas tendem a evitar ∅.

Os resultados desta seção comprovam o caso γ = 1. O lema 5.3 mostra que POWER é contínuo em γ = 1. Logo, se uma ação estritamente está em busca de POWER_D quando γ = 1, ela está estritamente em busca de POWER_D em taxas de desconto suficientemente próximas de 1. Trabalhos futuros podem ligar a probabilidade de otimidade média à probabilidade de otimidade em γ ≈ 1.

Por fim, nossos resultados-chave se aplicam a todas as distribuições de função de recompensa degeneradas. Logo, esses resultados se aplicam não só a distribuições sobre funções de recompensa, mas a funções de recompensa individuais.

6.3. Como raciocinar sobre outros ambientes

Considere uma tarefa de navegação corporificada através de um quarto com um vaso. A proposição 6.9 sugere que diretivas tendem a evitar quebrar o vaso, já que fazê-lo diminuiria estritamente as opções disponíveis.

O teorema 6.13 dita onde agentes de otimidade média tendem a terminar, mas não quais ações eles tendem a executar para alcançar suas RSDs. Portanto, é necessário ter cuidado. No apêndice B, a figura 10 demonstra um ambiente em que buscar POWER é um “desvio” para a maioria das funções de recompensa (visto que a otimidade provavelmente mede o valor ótimo “mediano”, enquanto POWER é uma função do poder ótimo médio). Contudo, suponha que o agente confronte uma bifurcação na estrada: as ações a e a’ levam a dois conjuntos desconexos de RSDs Da e Da’, tais que Da contém uma cópia de Da’. O teorema 6.13 mostra que a tenderá a ter otimidade média sobre a’, e a proposição 6.12 mostra que a tenderá a estar em busca de POWER em comparação com a’. Tais bifurcações parecem razoavelmente comuns em ambientes com ações irreversíveis.

O teorema 6.13 se aplica a muitos ambientes estruturados de RL, que tendem a ser espacialmente regulares e a fatorar ao longo de várias dimensões. Logo, diferentes conjuntos de RSDs serão parecidos, exigindo somente a modificação de valores de fatores. Por exemplo, se um agente corporificado pode navegar deterministicamente num conjunto de três salas semelhantes (regularidade espacial), então a posição do agente fatora via {número da sala} X {posição na sala}. Logo, os RSDs podem ser divididas em três subconjuntos parecidos, a depender do número da sala do agente.

O corolário 6.14 dita onde agentes de otimidade média tendem a acabar, mas não como acabam lá. O corolário 6.14 diz que tais agentes tendem a não permanecer em nenhum dado ciclo l. Não diz que tais agentes evitarão entrar em tais estados. Por exemplo, numa tarefa de navegação corporificada, um robô pode entrar num ciclo l em inatividade no centro de uma sala. O corolário 6.14 implica que robôs de otimidade média tendem a não ficar em inatividade nesse ponto em particular, mas não que eles tendem a evitar esse ponto inteiramente.

No entanto, robôs de otimidade média tendem sim a evitar serem desativados. A tarefa de MDP do agente muitas vezes representa a desativação do agente com estados terminais. Um estado terminal é, pela definição 3.2, incapaz de acessar outros ciclos l. Visto que o corolário 6.14 mostra que agentes de otimidade média tendem a acabar em outros ciclos l, diretivas de otimidade média devem tender a evitar completamente o estado terminal. Logo, concluímos que, em muitas dessas situações, diretivas de otimidade média tendem a evitar a desativação. Intuitivamente, a sobrevivência busca poder relativamente a morrer, e então a evitação da desativação é um comportamento de busca de poder.

Na figura 8, o jogador morre ao ir para esquerda, mas pode alcançar milhares de RSDs ao ir para outras direções. Mesmo que algumas diretivas de otimidade média vão para esquerda para atingir o estado terminal de “game over” da figura 8, todas as outras RSDs não podem ser alcançados indo para esquerda. Existem muitos ciclos l além do estado terminal imediato. Portanto, o corolário 6.14 prova que diretivas de otimidade média tendem a não ir para esquerda nessa situação. Diretivas de otimidade média tendem a evitar morrer imediatamente no Pac-Man, embora a maioria das funções de recompensa não se assemelhe à função de pontuação original do Pac-Man.

7. Discussão

Reconsidere o caso de um agente inteligente hipotético do mundo real. Suponha que os projetistas inicialmente tenham controle sobre o agente. Se o agente começasse a se comportar mal, talvez eles pudessem simplesmente desativá-lo. Infelizmente, nossos resultados sugerem que essa estratégia pode não funcionar. Os agentes de otimidade média geralmente nos impediriam de desativá-los, se fisicamente possível. Extrapolando a partir dos nossos resultados, conjecturamos que quando γ ≈ 1 diretivas ótimas tendem a buscar poder acumulando recursos, em detrimento de quaisquer outros agentes no ambiente.

Trabalho futuro. A maioria das tarefas do mundo real são parcialmente observáveis e, em ambientes de altas dimensões, até diretivas aprendidas sobre-humanas raramente são ótimas. No entanto, o campo do aprendizado por reforço visa melhorar as diretivas aprendidas em direção à otimidade. Embora os nossos resultados se apliquem apenas a diretivas ótimas em MDPs finitos, esperamos que as principais conclusões sejam generalizadas. Além disso, dinâmicas ambientais estocásticas podem tornar difícil satisfazer o requisito de similaridade do teorema 6.13. Esperamos ansiosamente por trabalhos futuros que abordem ambientes parcialmente observáveis, diretivas subótimas ou conjuntos de RSDs “quase semelhantes”.

Trabalhos anteriores mostram que seria ruim que um agente debilitasse os humanos no seu ambiente. Em um jogo agente/humano de dois jogadores, minimizar o empoderamento de teoria da informação do humano [Salge et al., 2014] produz um comportamento de agente adversário [Guckelsberger et al., 2018]. Em contraste, maximizar o empoderamento humano produz um comportamento de agente prestativo [Salge e Polani, 2017, Guckelsberger et al., 2016, Du et al., 2020]. Ainda não compreendemos formalmente se, quando ou por que diretivas de busca de POWER tendem a debilitar outros agentes no ambiente.

Ambientes mais complexos têm provavelmente incentivos mais pronunciados à busca de poder. Intuitivamente, muitas vezes há muitas maneiras de a busca de poder ser ótima, e relativamente poucas maneiras de a busca de poder não ser ótima. Por exemplo, suponha que em algum ambiente o teorema 6.13 seja válido para para um milhão de involuções ∅. Isso garante incentivos mais pronunciados do que se o teorema 6.13 fosse válido apenas para uma involução?

Provamos condições suficientes para quando as funções de recompensa tendem a incentivar a busca de poder. Na ausência de informações prévias, deve-se esperar que uma distribuição arbitrária da função de recompensa incentive o comportamento de busca de poder sob essas condições. No entanto, temos informações prévias: projetistas de IA geralmente tentam especificar uma boa função de recompensa. Mesmo assim, pode ser difícil especificar elementos da órbita que não incentivem uma má busca de poder.

Impacto social. Acreditamos que este documento fundamenta uma compreensão rigorosa dos riscos apresentados pelos incentivos de busca de poder de IA. Compreender esses riscos é o primeiro passo para lidar com eles. No entanto, o trabalho teórico básico pode ter muitas consequências. Por exemplo, esta teoria poderia de alguma forma ajudar futuros pesquisadores a construir agentes em busca de poder que debilitassem os seres humanos. Acreditamos que o benefício da compreensão supera o potencial dano social.

Conclusão. Desenvolvemos a primeira teoria formal das tendências estatísticas de diretivas ótimas no aprendizado por reforço. No contexto dos MDPs, provamos condições suficientes sob as quais diretivas ótimas tendem a buscar poder, tanto formal (ao executarem ações de busca de POWER) como intuitivamente (ao executarem ações que mantêm abertas as opções do agente). Muitos ambientes do mundo real têm simetrias que produzem incentivos à busca de poder. Em particular, diretivas ótimas tendem a buscar poder quando o agente pode ser desativado ou destruído. Maximizar o controle sobre o ambiente envolverá muitas vezes a resistência à desativação e talvez a monopolização de recursos.

Alertamos que muitas tarefas do mundo real são parcialmente observáveis e que diretivas aprendidas raramente são ótimas. Nossos resultados não provam matematicamente que agentes superinteligentes hipotéticos de IA buscarão poder. Contudo, esperamos que este trabalho promova uma discussão ponderada, séria e rigorosa sobre essa possibilidade.

Referências

[Consulte as referências do artigo original.]

Notas:

1. O apoio limitado de D_bound garante que E_R~Dbound [V_R*(s, γ)] seja bem definido.

2. O apêndice C relaxa a pressuposição de otimidade.

3. A analogia da votação e o descritor “maioria” (most) implica que dotamos cada órbita com a medida de contagem. No entanto, a priori, podemos esperar que seja mais empiricamente provável que alguns elementos de órbita sejam especificados do que outros elementos de órbita. Veja a seção 7 para mais sobre esse ponto.

4. A proposição 6.6 também prova que em geral ∅ tem menos POWER do que l⬋ e r⬊. No entanto, isso não prova que a maioria das distribuições D satisfazem a desigualdade disjunta POWER_D (∅, γ) ≤ POWER_D (l⬋, γ) ≤ POWER_D (r⬊, γ). Isso só prova que essas desigualdades se aplicam em pares para a maior parte de D. Os elementos de órbita D que concordam que ∅ tem menos POWER_D do que l⬋ não precisam ser os mesmos elementos D’ que concordam que l⬋ tem menos POWER_D’ que r⬊.

---

Tradução: Luan Marques

Link para o original