Blog

De Chris Olah, Nick Cammarata, Ludwig Schubert, Gabriel Goh, Michael Petrov e Shan Carter. 10 de março de 2020.

Estudando as conexões entre os neurônios, podemos descobrir algoritmos significativos nos pesos das redes neurais.

Muitos pontos de transição importantes na história da ciência foram momentos em que a ciência “ampliou”. Nestes pontos, desenvolvemos uma visualização ou ferramenta que nos permite ver o mundo com um novo nível de detalhe, e um novo campo da ciência se desenvolve para estudar o mundo através desta lente.

Por exemplo, os microscópios nos permitem ver as células, levando à biologia celular. A ciência ampliou. Várias técnicas, incluindo a cristalografia de raios X, nos permitem ver o DNA, levando à revolução molecular. A ciência ampliou. Teoria atômica. Partículas subatômicas. Neurociência. A ciência ampliou.

Estas transições não foram apenas uma mudança na precisão: foram mudanças qualitativas naquilo que são os objetos da pesquisa científica. Por exemplo, a biologia celular não é apenas uma zoologia mais cuidadosa. É um novo tipo de investigação que muda dramaticamente o que podemos compreender.

Os exemplos famosos deste fenómeno aconteceram numa escala muito grande, mas também pode ser a mudança mais modesta de uma pequena comunidade de pesquisa que percebeu que agora pode estudar o seu tópico num nível de detalhe mais refinado.

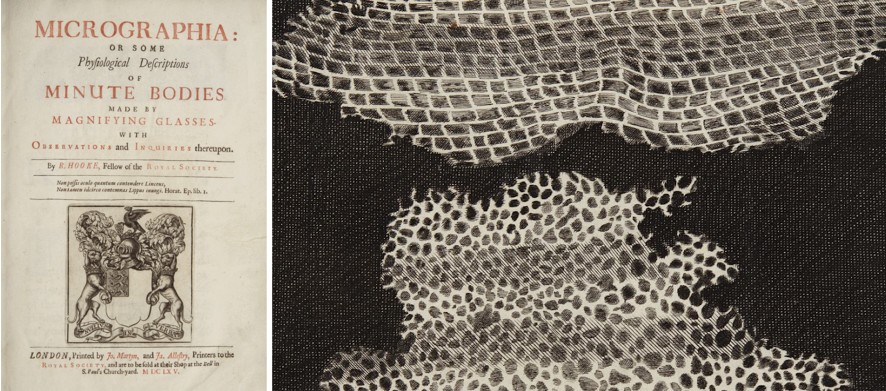
Assim como o primeiro microscópio sugeria um novo mundo de células e microorganismos, as visualizações de redes neurais artificiais revelaram sugestões tentadoras e vislumbres de um rico mundo interior dentro dos nossos modelos (por exemplo, [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]). Isso nos levou a perguntar: será possível que o aprendizado profundo esteja num ponto de transição semelhante, embora mais modesto?

A maior parte dos trabalhos sobre interpretabilidade visa fornecer explicações simples do comportamento de uma rede neural inteira. Mas e se, em vez disso, adotarmos uma abordagem inspirada na neurociência ou na biologia celular: uma abordagem de ampliação? E se tratássemos neurônios individuais, até mesmo pesos individuais, como dignos de investigação séria? E se estivéssemos dispostos a gastar milhares de horas rastreando cada neurônio e suas conexões? Que tipo de imagem das redes neurais surgiria?

Em contraste com a imagem típica das redes neurais como uma caixa-preta, ficamos surpresos com o quão acessível a rede é nesta escala. Não apenas os neurônios parecem compreensíveis (mesmo aqueles que inicialmente pareciam inescrutáveis), mas também os “circuitos” de conexões entre eles parecem ser algoritmos significativos que correspondem a fatos sobre o mundo. Você pode observar um detector de círculos sendo montado a partir de curvas. Você pode ver a cabeça de um cachorro sendo montada a partir de olhos, focinho, pelos e língua. Você pode observar como um carro é composto por rodas e janelas. Você pode até encontrar circuitos que implementam lógica simples: casos em que a rede implementa AND, OR ou XOR em características visuais de alto nível.

Este ensaio introdutório oferece uma visão geral de alto nível do nosso pensamento e alguns dos princípios de trabalho que consideramos úteis nesta linha de pesquisa. Em artigos futuros, nós e nossos colaboradores publicaremos explorações detalhadas deste mundo interior.

Mas a verdade é que apenas arranhamos a superfície da compreensão de um único modelo de visão. Se essas questões ressoam com você, você está convidado a se juntar a nós e aos nossos colaboradores no projeto Circuits, uma colaboração científica aberta hospedada no Distill slack.

Três alegações especulativas

Uma das primeiras articulações de algo que se aproxima da teoria celular moderna foram três alegações de Theodor Schwann – que você talvez conheça pelas células de Schwann – em 1839:

As alegações de Schwann sobre as células

• Alegação 1: a célula é a unidade de estrutura, fisiologia e organização dos seres vivos.
• Alegação 2: a célula mantém uma existência dupla como uma entidade distinta e um bloco de construção na edificação dos organismos.
• Alegação 3: as células se formam pela formação de células livres, semelhante à formação de cristais.

As duas primeiras alegações provavelmente são familiares, persistindo na teoria celular moderna. A terceira provavelmente não é familiar, pois se revelou terrivelmente errada.

Acreditamos que há muito valor em articular uma versão forte de algo que podemos acreditar ser verdadeiro, mesmo que possa ser falso como a terceira alegação de Schwann. Com esse espírito, oferecemos três alegações sobre redes neurais. Pretendem ser tanto alegações empíricas sobre a natureza das redes neurais como também afirmações normativas sobre como é útil compreendê-las.

Três alegações especulativas sobre redes neurais

Alegação 1: Características. Características são a unidade fundamental das redes neurais. Elas correspondem a direções.¹ Estas características podem ser rigorosamente estudadas e compreendidas.

Alegação 2: Circuitos. As características são conectadas por pesos, formando circuitos.² Estes circuitos também podem ser rigorosamente estudados e compreendidos.

Alegação 3: Universalidade. Características e circuitos análogos se formam em modelos e tarefas.

Essas alegações são deliberadamente especulativas. Elas também não são totalmente novas: alegações como (1) e (3) foram sugeridas antes, como discutiremos com mais profundidade abaixo.

Mas acreditamos que é importante considerar essas alegações porque, se forem verdadeiras, poderão formar a base de um novo campo “ampliado” da interpretabilidade. Nas seções a seguir, discutiremos cada uma delas individualmente e apresentaremos algumas das evidências que nos levaram a acreditar que elas poderiam ser verdadeiras.

Alegação 1: características

As características são a unidade fundamental das redes neurais. Elas correspondem a direções. Elas podem ser rigorosamente estudadas e compreendidas.

Acreditamos que as redes neurais consistem em características significativas e compreensíveis. As camadas iniciais contêm características como detectores de bordas ou curvas, enquanto as camadas posteriores possuem características como detectores de orelhas caídas ou detectores de rodas. A comunidade está dividida sobre se isso é verdade. Embora muitos pesquisadores tratem a existência de neurônios significativos como um fato quase trivial – há até uma pequena literatura que os estuda [15, 2, 16, 17, 4, 18, 19] — muitos outros são profundamente céticos e acreditam que casos anteriores de neurônios que pareciam rastrear variáveis ​​latentes significativas estavam errados [20, 21, 22, 23, 24].³ No entanto, milhares de horas de estudo de neurônios individuais nos levaram a acreditar que o caso típico é que os neurônios (ou, em alguns casos, outras direções no espaço vetorial de ativações neuronais) são compreensíveis.

É claro que ser compreensível não significa ser simples ou facilmente compreensível. Muitos neurônios são inicialmente misteriosos e não seguem nossas suposições a priori sobre quais características podem existir! No entanto, a nossa experiência é que normalmente há uma explicação simples por trás desses neurônios, e que na verdade eles estão fazendo algo bastante natural. Por exemplo, inicialmente ficamos confusos com detectores de alta-baixa frequência (discutidos abaixo), mas, em retrospecto, eles são simples e elegantes.

Este ensaio introdutório fornecerá apenas uma visão geral de alguns exemplos que consideramos ilustrativos, mas será seguido por análises profundas que caracterizam cuidadosamente as características individuais e por visões gerais amplas que esboçam todas as características que entendemos existir. Tomaremos nossos exemplos do InceptionV1 [26] por enquanto, mas acredito que essas afirmações sejam válidas de maneira geral e discutiremos outros modelos na seção final sobre universalidade.

Independentemente de estarmos certos ou errados sobre características significativas, acreditamos que esta é uma questão importante para a comunidade resolver. Esperamos que a introdução de vários exemplos específicos cuidadosamente explorados de características aparentemente compreensíveis ajude a avançar o diálogo.

Exemplo 1: detectores de curvas

Neurônios detectores de curvas podem ser encontrados em todos os modelos de visão não triviais que examinamos cuidadosamente. Essas unidades são interessantes porque ultrapassam a fronteira entre características que a comunidade concorda que existem (p. ex., detectores de bordas) e características sobre as quais há um ceticismo significativo (p. ex., características de alto nível como orelhas, automóveis e rostos).

Vamos nos concentrar nos detectores de curvas na camada mixed3b, uma camada inicial do InceptionV1. Essas unidades responderam a linhas curvas e limites com raio de cerca de 60 pixels. Elas também são ligeiramente excitadas adicionalmente por linhas perpendiculares ao longo do limite da curva e preferem que os dois lados da curva tenham cores diferentes.

Os detectores de curvas são encontrados em famílias de unidades, com cada membro da família detectando a mesma característica de curvas em uma orientação diferente. Juntos, eles abrangem toda a gama de orientações.

É importante distinguir os detectores de curvas de outras unidades que podem parecer superficialmente semelhantes. Em particular, existem muitas unidades que utilizam curvas para detectar um subcomponente curvo (p. ex., círculos, espirais, curvas S, formato de ampulheta, curvatura 3D, …). Existem também unidades que respondem a formas relacionadas a curvas, como linhas ou cantos agudos. Não consideramos essas unidades detectores de curvas.

Mas será que esses “detectores de curvas” estão realmente detectando curvas? Dedicaremos um artigo inteiro para explorar isso em profundidade, mas o resumo é que achamos que a evidência é bastante forte.

Oferecemos sete argumentos, descritos abaixo. Vale a pena notar que nenhum desses argumentos é específico a curvas: eles também são um kit de ferramentas útil e geral para testar nossa compreensão de outras características. Vários desses argumentos — exemplos de conjuntos de dados, exemplos sintéticos e ajustar curvas — são métodos clássicos da neurociência visual (p. ex., [27]). Os últimos três argumentos são baseados em circuitos, que discutiremos na próxima seção.

Argumento 1: visualização de características

Otimizar a entrada para fazer com que os detectores de curvas se ativem de forma confiável produz curvas. Isso estabelece uma ligação causal, uma vez que tudo na imagem resultante foi adicionado para fazer com que o neurônio se ative mais.
Você pode aprender mais sobre a visualização de características aqui .

Argumento 2: exemplos de conjuntos de dados

As imagens do ImageNet que fazem com que esses neurônios se ativem fortemente são curvas confiáveis ​​na orientação esperada. As imagens que fazem com que se ativem moderadamente são geralmente curvas menos perfeitas ou curvas fora de orientação.

Argumento 3: exemplos sintéticos

Os detectores de curvas respondem conforme o esperado a uma variedade de imagens de curvas sintéticas criadas com orientações, curvaturas e fundos variados. Eles se ativam apenas perto da orientação esperada e não se ativam com força em linhas retas ou cantos agudos.

Argumento 4: ajuste conjunto

Se pegarmos exemplos de conjuntos de dados que fazem um neurônio se ativar e girá-los, eles gradualmente param de se ativar e os detectores de curvas na próxima orientação começam a se ativar. Isso mostra que eles detectam versões rotacionadas da mesma coisa. Juntos, eles agrupam todos os 360 graus de orientações potenciais.

Argumento 5: implementação de características (argumento baseado em circuitos)

Observando o circuito que constrói os detectores de curvas, podemos ler um algoritmo de detecção de curvas a partir dos pesos. Também não vemos nada que sugira uma segunda causa alternativa de ativação, embora existam muitos pesos menores cujo papel não entendemos.

Argumento 6: uso de características (argumento baseado em circuitos)

Os clientes a jusante dos detectores de curvas são características que envolvem curvas naturalmente (p. ex., círculos, curvatura 3D, espirais…). Os detectores de curva são utilizados por esses clientes da maneira esperada.

Argumento 7: circuitos manuscritos (argumento baseado em circuitos)

Com base em nossa compreensão de como os detectores de curvas são implementados, podemos fazer uma reimplementação de sala limpa, definindo manualmente todos os pesos para reimplementar a detecção de curvas. Esses pesos são um algoritmo de detecção de curvas compreensível e imitam significativamente os detectores de curvas originais.

Os argumentos acima não excluem totalmente a possibilidade de algum caso secundário raro em que os detectores de curvas se ativam para um tipo diferente de estímulo. Mas eles parecem estabelecer que (1) as curvas fazem com que esses neurônios se ativem, (2) cada unidade responde a curvas em diferentes orientações angulares e, (3) se houver outros estímulos que os façam se ativar, esses estímulos são raros ou causam ativações mais fracas. De forma mais geral, esses argumentos parecem satisfazer os padrões evidenciais que entendemos serem utilizados na neurociência, que estabeleceu tradições e conhecimento institucional sobre como avaliar tais alegações.

Todos esses argumentos serão explorados em detalhes nos artigos posteriores sobre detectores de curvas e circuitos de detecção de curvas.

Exemplo 2: detectores de alta-baixa frequência

Os detectores de curvas são um tipo de característica intuitiva, o tipo de característica que se poderia imaginar que existe a priori em redes neurais. Dado que estão presentes, não é surpreendente que possamos entendê-las. Mas e as características que não são intuitivas? Também podemos entendê-las? Acreditamos que sim.

Os detectores de alta-baixa frequência são um exemplo de um tipo de característica menos intuitiva. Nós as encontramos na visão inicial e, uma vez que você entende o que estão fazendo, elas são bastante simples. Eles procuram padrões de baixa frequência em um lado do campo receptivo e padrões de alta frequência no outro lado. Assim como os detectores de curvas, os detectores de alta-baixa frequência são encontrados em famílias de características que procuram a mesma coisa em diferentes orientações.

Por que os detectores de alta-baixa frequência são úteis para a rede? Eles parecem ser uma das várias heurísticas para detectar os limites dos objetos, especialmente quando o fundo está fora de foco. Em um artigo posterior, exploraremos como eles são usados ​​na construção de detectores de limites sofisticados.

(Uma esperança que alguns pesquisadores têm em relação à interpretabilidade é que a compreensão dos modelos seja capaz de nos ensinar melhores abstrações para pensar sobre o mundo [28]. Os detectores de alta-baixa frequência são, talvez, um exemplo de um pequeno sucesso nisso: uma característica visual natural e útil que não previmos antecipadamente.)

Todas as sete técnicas que usamos para interrogar neurônios de curvas também podem ser usadas para estudar neurônios de alta-baixa frequência com alguns ajustes — p. ex., renderizando exemplos sintéticos de alta-baixa frequência. Mais uma vez, acreditamos que esses argumentos, em conjunto, fornecem um forte apoio à ideia de que isso é realmente uma família de detectores de contraste de alta-baixa frequência.

Exemplo 3: detector de cabeça de cachorro invariante à pose

Tanto os detectores de curvas quanto os detectores de alta-baixa frequência são características visuais de baixo nível, encontradas nas primeiras camadas do InceptionV1. E quanto a características mais complexas e de alto nível?

Vamos considerar esta unidade que acreditamos ser um detector de cães invariante à pose. Como acontece com qualquer neurônio, podemos criar uma visualização de características e coletar exemplos de conjuntos de dados. Se você observar a visualização da característica, a geometria… não é possível, mas é muito informativa sobre o que está procurando e os exemplos do conjunto de dados validam isso.

É importante notar que a combinação de visualização de características e exemplos de conjuntos de dados por si só já é um argumento bastante forte. A visualização de características estabelece uma ligação causal, enquanto os exemplos de conjuntos de dados testam o uso do neurônio na prática e se há um segundo tipo de estímulo ao qual ele reage. Mas podemos trazer todas as nossas outras abordagens para analisar um neurônio novamente. Por exemplo, podemos usar um modelo 3D para gerar imagens sintéticas de cabeças de cachorro de diferentes ângulos.

Ao mesmo tempo, algumas das abordagens que enfatizamos até agora exigem muito esforço para essas características mais abstratas e de nível superior. Felizmente, nossos argumentos baseados em circuitos — que discutiremos mais em breve — continuarão a ser fáceis de aplicar e nos fornecerão ferramentas realmente poderosas para compreender e testar características de alto nível que não exigem muito esforço.

Neurônios polissemânticos

Este ensaio pode estar lhe dando uma imagem excessivamente otimista: talvez cada neurônio produza um conceito agradável e compreensível para os humanos se for investigado seriamente?

Infelizmente, esse não é o caso. As redes neurais geralmente contêm “neurônios polissemânticos” que respondem a múltiplas entradas não relacionadas. Por exemplo, o InceptionV1 contém um neurônio que responde a rostos de gatos, frentes de carros e pernas de gatos.

Para ser claro, esse neurônio não está respondendo a alguns pontos em comum entre carros e rostos de gatos. A visualização de características nos mostra que ele está procurando os olhos e bigodes de um gato, pernas peludas e frentes brilhantes de carros, e não alguma característica compartilhada sutil.

Ainda podemos estudar tais características, caracterizando cada caso diferente que eles ativam, e raciocinar sobre seus circuitos até certo ponto. Apesar disso, os neurônios polissemânticos são um grande desafio para a pauta dos circuitos, limitando significativamente a nossa capacidade de raciocinar sobre redes neurais.⁴ Nossa esperança é que seja possível resolver neurônios polissemânticos, talvez “desdobrando” uma rede para transformar neurônios polissemânticos em características puras, ou treinando redes para não exibirem polissemanticidade em primeiro lugar. Esse é essencialmente o problema estudado na literatura de desemaranhar representações, embora atualmente essa literatura tenda a se concentrar em características conhecidas nos espaços latentes dos modelos generativos.

Uma pergunta natural a ser feita é por que os neurônios polissemânticos se formam? Na próxima seção, veremos que eles parecem resultar de um fenômeno que chamamos de “sobreposição”, no qual um circuito espalha uma característica por muitos neurônios, presumivelmente para incluir mais características no número limitado de neurônios que tem disponível.

Alegação 2: circuitos

As características são conectadas por pesos, formando circuitos.
Esses circuitos também podem ser rigorosamente estudados e compreendidos.

Todos os neurônios da nossa rede são formados a partir de combinações lineares de neurônios da camada anterior, seguida por ReLU. Se pudermos compreender as características em ambas as camadas, não deveríamos também ser capazes de compreender as conexões entre elas? Para explorar isso, achamos útil estudar circuitos: subgrafos da rede, que consistem em um conjunto de características estreitamente interligadas e os pesos entre elas.

O que é notável é quão tratáveis ​​e significativos esses circuitos parecem ser como objetos de estudo. Quando começamos a procurar, esperávamos encontrar algo bastante confuso. Em vez disso, encontramos belas estruturas ricas, muitas vezes com simetria. Depois de entender quais características eles estão conectando, os pesos numéricos de pontos flutuantes individuais em sua rede neural se tornam significativos! Você pode literalmente ler algoritmos significativos a partir dos pesos.

Vamos considerar alguns exemplos.

Circuito 1: detectores de curvas

Na seção anterior, discutimos detectores de curvas, uma família de unidades que detectam curvas em diferentes orientações angulares. Nesta seção, exploraremos como os detectores de curvas são implementados a partir de características anteriores e se conectam ao restante do modelo.

Os detectores de curvas são implementados principalmente a partir de detectores de curvas e detectores de linhas anteriores menos sofisticados. Esses detectores de curvas são usados ​​na próxima camada para criar geometria 3D e detectores de formas complexas. Claro, há uma longa cauda de conexões menores com outras características, mas essa parece ser a história principal.

Nesta introdução, focaremos na interação dos detectores de curvas iniciais e de nossos detectores de curvas completas.

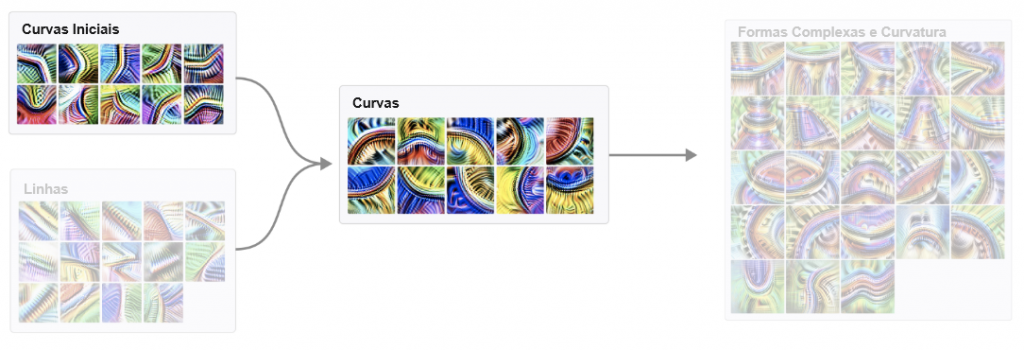
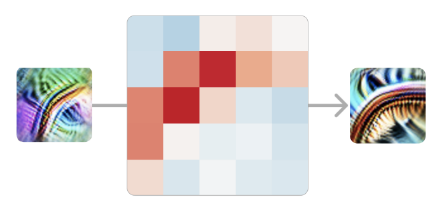
Vamos focar ainda mais e ver como um único detector de curvas iniciais se conecta a um detector de curvas mais sofisticado na mesma orientação.

Neste caso, nosso modelo está implementando uma convolução 5×5; então os pesos que ligam estes dois neurônios são um conjunto de pesos 5×5, que pode ser positivo ou negativo.⁵ Um peso positivo significa que, se o neurônio anterior se ativa nesta posição, ele excita o neurônio tardio. Por outro lado, um peso negativo significaria que o inibe.

O que vemos são pesos positivos fortes, dispostos na forma do detector de curvas. Podemos pensar nisso como significando que, em cada ponto ao longo da curva, o nosso detector de curvas está à procura de uma “curva tangente” utilizando o detector de curvas anteriores.

Isso é verdade para cada par de detectores de curvas iniciais e completas em orientações semelhantes. Em cada ponto ao longo da curva, ele detecta a curva numa orientação semelhante. Da mesma forma, as curvas na orientação oposta são inibitórias em todos os pontos ao longo da curva.

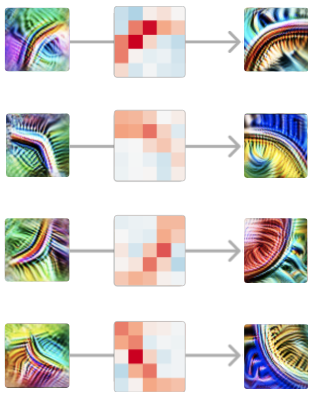
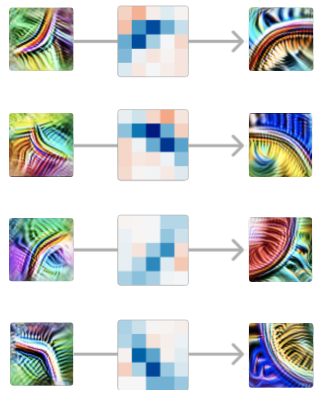
Vale a pena refletir aqui que estamos analisando os pesos das redes neurais e eles são significativos.

E a estrutura fica mais rica quanto mais você olha mais de perto. Por exemplo, se você observar um detector de curvas iniciais e um detector de curvas completas em orientação semelhante, mas não exatamente na mesma, muitas vezes poderá ver que eles têm pesos positivos mais fortes no lado da curva com o qual estão mais alinhados.

Também vale a pena notar como os pesos giram com a orientação do detector de curvas. A simetria do problema é refletida como uma simetria nos pesos. Chamamos os circuitos que exibem esse fenômeno de “circuito equivariante” e discutiremos isso em profundidade em um artigo posterior .

Circuito 2: detecção orientada de cabeça de cachorro

O circuito detector de curvas é um circuito de baixo nível e abrange apenas duas camadas. Nesta seção, discutiremos um circuito de nível superior abrangendo quatro camadas. Este circuito também nos ensinará como as redes neurais implementam invariâncias sofisticadas.

Lembre-se de que grande parte do que um modelo do ImageNet precisa fazer é distinguir diferentes animais. Em particular, tem de distinguir entre cem espécies diferentes de cães! E assim, sem surpresa, desenvolve um grande número de neurônios dedicados ao reconhecimento de características relacionadas com cachorros, incluindo cabeças.

Dentro deste sistema de “reconhecimento de cachorros”, um circuito nos parece particularmente interessante: uma coleção de neurônios que lidam com cabeças de cachorros voltadas para a esquerda e cabeças de cachorros voltadas para a direita. Ao longo de três camadas, a rede mantém dois caminhos espelhados, detectando unidades análogas voltadas para a esquerda e para a direita. A cada etapa, essas vias tentam se inibir mutuamente, aumentando o contraste. Finalmente, cria neurônios invariantes que respondem a ambas as vias.

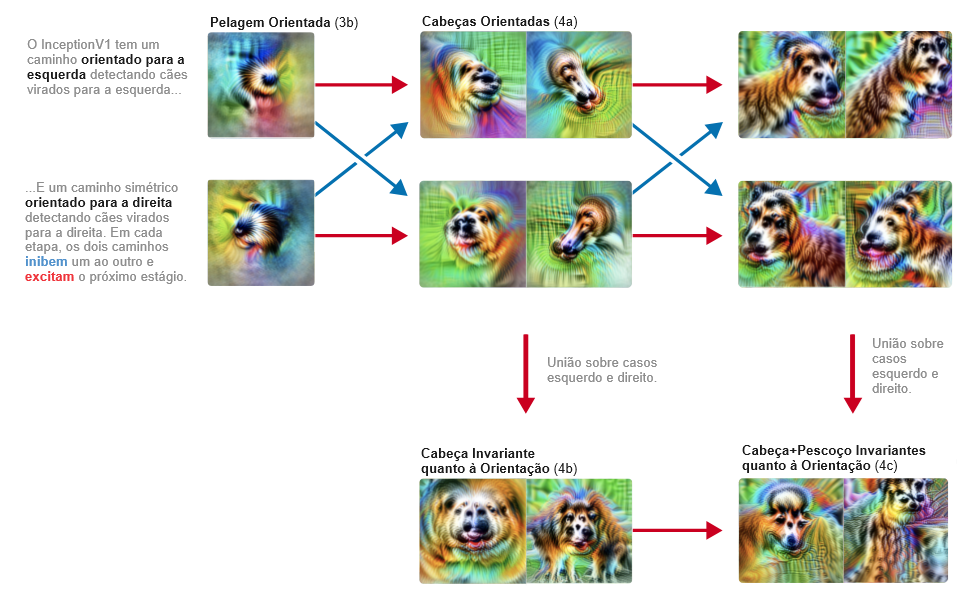
Chamamos esse padrão de “união sobre casos”. A rede detecta separadamente dois casos (esquerdo e direito) e então faz uma união sobre eles para criar unidades invariantes “multifacetadas” [29]. Observe que, como as duas vias se inibem, esse circuito na verdade possui algumas propriedades semelhantes a XOR.

Esse circuito é impressionante porque a rede poderia facilmente ter feito algo muito menos sofisticado. Ele poderia facilmente criar neurônios invariáveis, não se importando muito com a localização dos olhos, pelos e focinho, e apenas procurando uma confusão deles juntos. Mas, em vez disso, a rede aprendeu a separar os casos esquerdo e direito e a tratá-los separadamente. Estamos um tanto surpresos que a descida gradiente possa aprender a fazer isso!⁶

Mas este resumo do circuito está apenas arranhando a superfície do que está acontecendo. Cada conexão entre neurônios é uma convolução; então também podemos observar onde um neurônio de entrada excita o próximo. E os modelos tendem a fazer o que você esperava com otimismo. Por exemplo, considere estas unidades “cabeça com pescoço”. A cabeça só é detectada no lado correto:

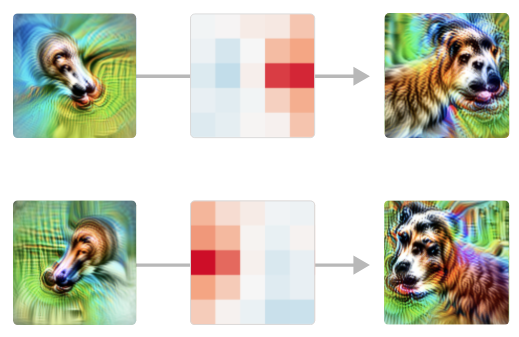
A etapa de união também é interessante de observar em detalhes. A rede não responde indiscriminadamente às cabeças nas duas orientações: as regiões de excitação se estendem do centro em direções diferentes dependendo da orientação, permitindo que os focinhos convirjam para o mesmo ponto.

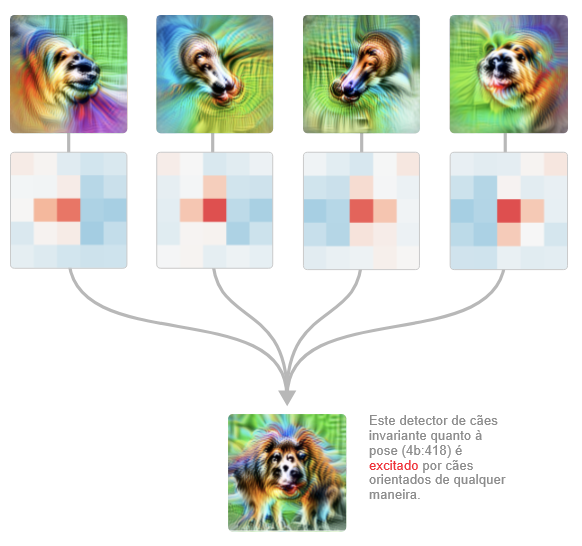
Há muito mais a dizer sobre este circuito, e por isso planejamos voltar a ele em um artigo futuro e analisá-lo com profundidade, inclusive testando nossa teoria do circuito editando os pesos.

Circuito 3: carros em sobreposição

Em mixed4c, uma camada intermediária do InceptionV1, há um neurônio de detecção de carros. Usando características das camadas anteriores, ele procura rodas na parte inferior da janela convolucional e janelas na parte superior.

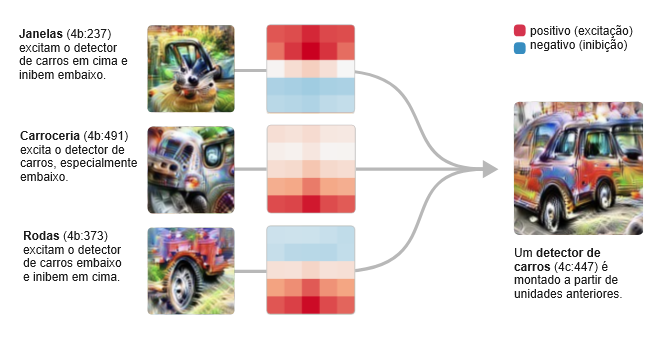
Mas então o modelo faz algo surpreendente. Em vez de criar outro detector puro de carros na camada seguinte, ele espalha a sua característica de carro por vários neurônios que parecem estar principalmente fazendo outra coisa, em particular, detectores de cães.

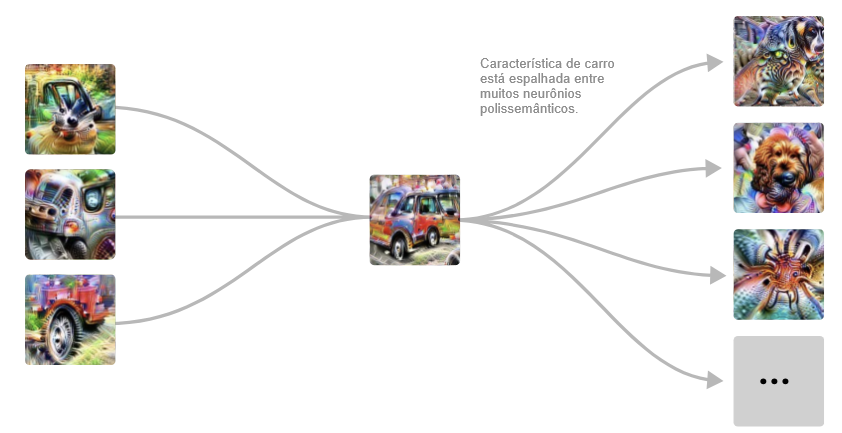
Este circuito sugere que os neurônios polissemânticos são, em certo sentido, deliberados. Ou seja, você poderia imaginar um mundo onde o processo de detecção de carros e cachorros estivesse profundamente interligado no modelo por algum motivo e, como resultado, os neurônios polissemânticos fossem difíceis de evitar. Mas o que estamos vendo aqui é que o modelo tinha um “neurônio puro” e depois o misturou com outras características.

Chamamos esse fenômeno de sobreposição.

Por que ele faria tal coisa? Acreditamos que a sobreposição permite que o modelo use menos neurônios, conservando-os para tarefas mais importantes. Contanto que carros e cachorros não ocorram simultaneamente, o modelo pode recuperar com precisão a característica do cachorro em uma camada posterior, permitindo armazenar a característica sem dedicar um neurônio.⁷

Motivos de circuitos

À medida que estudamos circuitos no InceptionV1 e outros modelos, vimos os mesmos padrões abstratos repetidamente. Equivariância, como vimos com os detectores de curvas. União sobre casos, como vimos com o detector de cabeça de cachorro invariante à pose. Sobreposição, como vimos com o detector de carros.

Na biologia, um motivo de circuitos [30] é um padrão recorrente em gráficos complexos, como redes de transcrição ou redes neurais biológicas. Os motivos são úteis porque a compreensão de um motivo pode dar aos pesquisadores vantagem em todos os grafos onde ele ocorre.

Achamos que é bastante provável que o estudo dos motivos seja importante na compreensão dos circuitos das redes neurais artificiais. No longo prazo, pode ser mais importante do que o estudo de circuitos individuais. Ao mesmo tempo, esperamos que as investigações dos motivos sejam bem-servidas, construindo primeiro uma base sólida de circuitos bem-compreendidos.

Alegação 3: universalidade

Características e circuitos análogos se formam em modelos e tarefas.

É um fato amplamente aceito que a primeira camada de modelos de visão treinados em imagens naturais aprenderá filtros de Gabor. Depois de aceitar que existem características significativas em camadas posteriores, seria realmente surpreendente que as mesmas características também se formassem em camadas além da primeira? E uma vez que você acredita que existem características análogas em múltiplas camadas, não seria natural que elas se conectassem da mesma maneira?

A universalidade (ou “aprendizado convergente”) das características já foi sugerida antes. Trabalhos anteriores mostraram que diferentes redes neurais podem desenvolver neurônios altamente correlacionados [31] e que eles aprendem representações semelhantes em camadas ocultas [32, 33]. Este trabalho parece altamente sugestivo, mas existem explicações alternativas para a formação de características análogas. Por exemplo, pode-se imaginar duas características – como um detector de textura de pele e um sofisticado detector de corpo de cachorro – sendo altamente correlacionadas, apesar de serem características importantes e diferentes. Adotando a perspectiva significativa dos céticos com relação às características, isso não parece definitivo.

Idealmente, gostaríamos de caracterizar várias características e depois demonstrar rigorosamente que essas características — e não apenas as correlacionadas — estão se formando em muitos modelos. Então, para estabelecer ainda mais a formação de circuitos análogos, seria desejável encontrar características análogas em várias camadas de múltiplos modelos e mostrar que a mesma estrutura de peso se forma entre elas em cada modelo.

Infelizmente, a única evidência que podemos oferecer hoje é anedótica: simplesmente ainda não investimos o suficiente no estudo comparativo de características e circuitos para dar respostas confiáveis. Apesar disso, observamos que algumas características de baixo nível parecem se formar em uma variedade de arquiteturas de modelos de visão (incluindo AlexNet, InceptionV1, InceptionV3 e redes residuais) e em modelos treinados no Places365 em vez do ImageNet. Também as observamos se formando repetidamente em redes convolucionais comuns treinadas do zero no ImageNet.

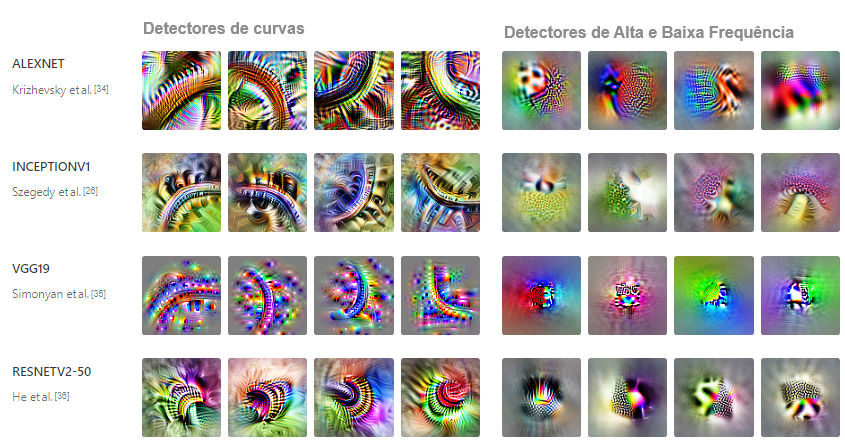
Esses resultados nos levaram a suspeitar que a hipótese da universalidade é provavelmente verdadeira, mas serão necessários mais trabalhos para compreender se a aparente universalidade de algumas características da visão de baixo nível é a exceção ou a regra.

Se for verificado que a hipótese da universalidade é amplamente verdadeira nas redes neurais, será tentador especular: poderão as redes neurais biológicas também aprender características semelhantes? Pesquisadores que trabalham na interseção entre neurociência e aprendizado profundo já mostraram que as unidades em modelos de visão artificial podem ser úteis para modelar neurônios biológicos [37, 38, 39]. E acredita-se que algumas das características que descobrimos em redes neurais artificiais, como detectores de curvas, também existam em redes neurais biológicas (por exemplo, [40, 41]). Isso parece ser um motivo significativo para otimismo.⁸

Focando no estudo dos circuitos, a universalidade é realmente necessária? Ao contrário das duas primeiras alegações, não seria completamente fatal para a pesquisa em circuitos se essa afirmação se revelasse falsa. Mas informa muito que tipo de pesquisa faz sentido. Introduzimos os circuitos como uma espécie de “biologia celular do aprendizado profundo”. Mas imagine um mundo onde cada espécie tivesse células com um conjunto completamente diferente de organelas e proteínas. Ainda faria sentido estudar as células em geral, ou nos limitaríamos ao estudo restrito de alguns tipos de espécies de células particularmente importantes? Da mesma forma, imagine o estudo da anatomia num mundo onde cada espécie de animal tivesse uma anatomia completamente não relacionada: estudaríamos seriamente outra coisa senão humanos e alguns animais domésticos?

Da mesma forma, a hipótese da universalidade determina que forma de pesquisa de circuitos faz sentido. Se isso fosse verdade no sentido mais forte, poderíamos imaginar uma espécie de “tabela periódica de características visuais” que observamos e catalogamos entre modelos. Por outro lado, se fosse em grande parte falso, precisaríamos nos concentrar num punhado de modelos de particular importância social e esperar que parassem de mudar todos os anos. Também pode haver mundos intermediários, onde algumas lições são transferidas entre modelos, mas outras precisam ser aprendidas do zero.

Interpretabilidade como ciência natural

A Estrutura das Revoluções Científicas de Thomas Kuhn [42]é um texto clássico sobre história e sociologia da ciência. Nele, Kuhn distingue entre “ciência normal”, em que uma comunidade científica tem um paradigma, e “ciência extraordinária”, em que uma comunidade carece de paradigma, seja porque nunca teve um, seja porque foi enfraquecida pela crise. Vale a pena notar que a “ciência extraordinária” não é um estado desejável: é um período em que os investigadores lutam para serem produtivos.

A descrição de Kuhn dos campos pré-paradigmáticos parece estranhamente uma reminiscência da interpretabilidade atual.⁹ Não há consenso sobre quais são os objetos de estudo, que métodos devemos utilizar para respondê-los ou como avaliar os resultados das pesquisas. Citando uma entrevista recente com Ian Goodfellow: “Em termos de interpretabilidade, penso que nem sequer temos as definições corretas”.[43]

Um aspecto particularmente desafiador de estar num campo pré-paradigmático é que não existe um senso comum de como avaliar o trabalho em termos de interpretabilidade. Existem duas propostas comuns para lidar com isso, com base nos padrões de campos adjacentes. Alguns pesquisadores, especialmente aqueles com experiência em aprendizado profundo, desejam um “referencial da interpretabilidade” que possa avaliar a eficácia de um método de interpretabilidade. Outros pesquisadores com experiência em Interação Humano-Computador podem desejar avaliar métodos de interpretabilidade por meio de estudos de usuários.

Mas a interpretabilidade também poderia tomar emprestado um terceiro paradigma: a ciência natural. Nessa visão, as redes neurais são um objeto de investigação empírica, talvez semelhante a um organismo na biologia. Tal trabalho tentaria fazer alegações empíricas sobre uma determinada rede, que poderiam ser mantidas no padrão da falsificabilidade.

Por que não vemos mais esse tipo de avaliação do trabalho em interpretabilidade e visualização?¹⁰ Especialmente considerando que há muitos trabalhos adjacentes de aprendizado de máquina que adotam essa estrutura! Uma razão pode ser que é muito difícil fazer afirmações resilientemente verdadeiras sobre o comportamento de uma rede neural como um todo. Elas são objetos incrivelmente complicados. Também é difícil formalizar quais seriam exatamente as declarações empíricas interessantes sobre elas. E assim, muitas vezes obtemos padrões de avaliação mais direcionados para saber se um método de interpretabilidade é útil, em vez de sabermos se estamos descobrindo alegações verdadeiras.

Os circuitos contornam esses desafios concentrando-se em pequenos subgrafos de uma rede neural para os quais é tratável uma investigação empírica rigorosa. Eles são muito falsificáveis: por exemplo, se você entende um circuito, deverá ser capaz de prever o que mudará se editar os pesos. Na verdade, para circuitos suficientemente pequenos, as afirmações sobre o seu comportamento se tornam questões de raciocínio matemático. É claro que o custo desse rigor é que as declarações sobre circuitos têm um escopo muito menor do que o comportamento geral do modelo. Mas parece que, com esforço suficiente, as afirmações sobre o comportamento do modelo poderiam ser decompostas em afirmações sobre circuitos. Se assim for, talvez os circuitos possam funcionar como uma espécie de base epistêmica para a interpretabilidade.

Considerações finais

Damos como certo que o microscópio é um importante instrumento científico. É praticamente um símbolo da ciência. Mas nem sempre foi assim, e os microscópios inicialmente não decolaram como ferramenta científica. Na verdade, eles parecem ter definhado por cerca de cinquenta anos. O ponto de viragem foi quando Robert Hooke publicou Micrographia¹, uma coleção de desenhos de coisas que ele viu usando um microscópio, incluindo a primeira imagem de uma célula.

Nossa impressão é que há certa aflição na comunidade da interpretabilidade por não sermos levados muito a sério. Que esta pesquisa é muito qualitativa. Que não é científica. Mas a lição do microscópio e da biologia celular é que talvez isso seja esperado. A descoberta das células foi resultado de uma pesquisa qualitativa. Isso não a impediu de mudar o mundo.

---

Glossário

Este ensaio introduz alguma nova terminologia e também usa alguma terminologia que não é comum. Para ajudar, disponibilizamos o seguinte glossário:

A Jusante / A Montante: em uma camada posterior / em uma camada anterior.

Característica: uma função escalar da entrada. Neste ensaio, as características da rede neural são direções e, muitas vezes, simplesmente neurônios individuais. Afirmamos que tais características em redes neurais são características tipicamente significativas que podem ser estudadas rigorosamente (Alegação 1).

Característica Polissemântica: uma característica que responde a múltiplas variáveis ​​latentes não relacionadas, como o neurônio gato/carro [4]. Isto pode ser visto como um caso especial de “características multifacetadas” [29] que respondem a vários casos diferentes, mas inclui características multifacetadas “reais”, como a cabeça de cachorro invariante à pose ou neurônios polissemânticos. Contraste com pura.

Característica Pura: uma característica que responde a apenas uma única variável latente. Compare com polissemântica.

Característica Significativa: uma característica que responde genuinamente a uma propriedade articulável da entrada, como a presença de uma curva ou de uma orelha caída. Características significativas ainda podem ser ruidosas ou imperfeitas.

Característica Universal: uma característica que se forma de modo confiável em diferentes modelos e tarefas.

Circuito: um subgrafo de uma rede neural. Os nós correspondem a neurônios ou direções (combinações lineares de neurônios). Dois nós terão uma aresta entre eles se estiverem em camadas adjacentes. As arestas têm pesos que são os pesos entre esses neurônios (ou n₁ Wn₂ ^T se os nós forem combinações lineares). Para camadas convolucionais, os pesos são matrizes 2D que representam os pesos para diferentes posições relativas das camadas.

Direção: uma combinação linear de neurônios em uma camada. Equivalentemente, um vetor na representação de uma camada. Uma direção pode ser um neurônio individual (que é uma direção básica do espaço vetorial). Para uma intuição sobre direções como um objeto, consulte Building Blocks [44] (em particular, a seção intitulada “What Does The Network See?”) e Atlas de ativação [13].

Equivariância: para equivariância no contexto de circuitos (p. ex., características equivariantes, circuitos equivariantes), consulte o artigo do circuito sobre equivariância. Para uma ideia mais geral de equivariância na matemática, consulte o artigo sobre mapa equivariante da Wikipédia.

Família: um conjunto de características encontradas em uma camada que detectam pequenas variações da mesma coisa. Por exemplo, os detectores de curvas existem em uma família que detecta curvas em diferentes orientações.

Motivo de Circuito: um padrão abstrato recorrente encontrado em circuitos, como equivariância ou união sobre casos. Inspirado no uso de motivos de circuitos na biologia dos sistemas [30].

Neurônio Cliente ou Característica Cliente: um neurônio em uma camada posterior que depende de um neurônio anterior específico. Por exemplo, um detector de círculos é um cliente de detectores de curvas.

Representação: o espaço vetorial formado pelas ativações de todos os neurônios de uma camada, com vetores da forma (ativação do neurônio 1, ativação do neurônio 2, …). Uma representação pode ser considerada como a coleção de todas as característica que existem em uma camada. Para obter uma intuição sobre representações em modelos de visão, consulte Atlas de Ativação [13].

Contribuições dos autores

Redação: o texto deste ensaio foi escrito principalmente por Christopher Olah, baseando-se extensivamente na pesquisa e no pensamento de toda a equipe do Clarity. Nick Cammarata esteve profundamente envolvido no desenvolvimento do enquadramento e na revisão do texto final.

Pesquisa: este ensaio articula temas que se desenvolveram como resultado de pesquisas de várias pessoas sobre como as redes neurais implementam características. Chris iniciou as tentativas iniciais de compreender as implementações mecanicistas dos neurônios em termos de seus pesos em 2018 e desenvolveu diversas ferramentas que possibilitaram essa linha de trabalho. Este trabalho foi ampliado por Gabriel Goh, que descobriu o primeiro do que hoje chamamos de motivos (usando pesos negativos para especialização), além de descrever os mecanismos por trás de vários neurônios. Neste ponto, Nick Cammarata assumiu esta linha de pesquisa para caracterizar circuitos muito maiores e mais profundos, expandir enormemente o número de neurônios que entendíamos mecanicamente e realizar caracterizações detalhadas e rigorosas de detectores de curvas. Nick também introduziu a conexão com a biologia dos sistemas. Ludwig Schubert realizou análises detalhadas de detectores de alta-baixa frequência. Chris deu conselhos de pesquisa e orientação durante todo o processo.

Infraestrutura: Michael Petrov, Shan Carter, Ludwig e Nick construíram uma variedade de ferramentas de infraestrutura que tornaram nossa pesquisa possível.

Nota Histórica

As ideias neste ensaio introdutório foram apresentadas anteriormente como uma palestra de Chris Olah no VISxAI 2019. Também foi apresentado informalmente no MILA, no Vector Institute, no Redwood Center for Neuroscience e em um workshop privado.

Agradecimentos

Todo o nosso trabalho de compreensão do InceptionV1 se deve a Alex Mordvintsev, cujas primeiras explorações de modelos de visão abriram caminhos que ainda seguimos. Estamos profundamente gratos a Nick Barry e Sophia Sanborn pelo seu profundo envolvimento nas possíveis conexões entre o nosso trabalho e a neurociência, e a Tom McGrath que apontou as semelhanças entre a “ciência pré-paradigmática” de Kuhn e o estado da interpretabilidade como um campo para nós. Os cuidadosos comentários e críticas de Brice Menard também foram inestimáveis ​​para aprimorar este ensaio.

Além do profundo envolvimento de Nick e Sophia, estamos mais gratos pelo envolvimento da comunidade neurocientífica conosco, especialmente no compartilhamento de lições duramente conquistadas sobre fraquezas metodológicas em nosso trabalho. Em particular, agradecemos Brian Wandell que nos incentivou em 2019 a não usar curvas de ajuste e a importância das famílias de neurônios, o que acreditamos ter tornado nosso trabalho muito mais forte. Também estamos muito gratos pelos comentários e apoio de Mareike Grotheer, Natalia Bilenko, Bruno Olshausen, Michael Eickenberg, Charles Frye, Philip Sabes, Paul Merolla, James Redd, Thong-Wei Koh e Ivan Alvarez. Achamos que temos muito a aprender com a comunidade da neurociência e estamos entusiasmados em continuar fazendo isso.

Um dos privilégios de trabalhar em circuitos tem sido a colaboração aberta e o feedback no canal #circuits do Distill Slack. Apreciamos especialmente o feedback detalhado que recebemos de Stefan Sietzen, Shahab Bakhtiari e Flora Liu (Stefan também apresentou muitas dessas ideias e estamos entusiasmados em ver seu trabalho em artigos futuros neste tópico!).

Beneficiamo-nos muito com os comentários de muitas pessoas sobre metaciência e questões de enquadramento em torno deste ensaio, mas apreciamos especialmente os comentários de Arvind Satyanarayan, Miles Brundage, Amanda Askell, Aaron Courville e Martin Wattenberg. Somos gratos a Taco Cohen, Tess Smidt e Sara Sabour pelos seus comentários extremamente úteis sobre equivariância. Somos gratos a Nikita Obidin, Nick Barry e Chelsea Voss pelas conversas úteis e referências sobre biologia dos sistemas e motivos de circuitos. (Nikita e Nick inicialmente apresentaram Nick Cammarata aos motivos de circuitos.) Finalmente, somos gratos pelo apoio institucional da OpenAI e pelo apoio e comentários de todos os nossos colegas e amigos em todas as instituições, incluindo Dario Amodei, Daniela Amodei, Jonathan Uesato , Laura Ball, Katarina Slama, Alethea Power, Jacob Hilton, Jacob Steinhardt, Tom Brown, Preetum Nakkiran, Ilya Sutskever, Ryan Lowe, Erin McCloskey, Eli Chen, Fred Hohman, Jason Yosinski, Pallavi Koppol, Reiichrio Nakano, Sam McCandlish, Daniel Dewey, Anna Goldie, Jochen Görtler, Hendrik Strobelt, Ravi Chunduru, Tom White, Roger Grosse, David Duvenaud, Daniel Burkhardt, Janelle Tam, Jeff Clune, Christian Szegedy, Alec Radford, Alex Ray, Evan Hubinger, Scott Gray, Augustus Odena, Mikhial Pavlov, Daniel Filan, Jascha Sohl-Dickstein e Kris Sankaran.

Notas de rodapé

1. Por “direção” queremos dizer uma combinação linear de neurônios em uma camada. Você pode pensar nisso como um vetor de direção no espaço vetorial das ativações dos neurônios em uma determinada camada. Geralmente, achamos mais útil falar sobre neurônios individuais, mas veremos que há alguns casos em que outras combinações são uma forma mais útil de analisar redes, especialmente quando os neurônios são “polissemânticos”. (Consulte o glossário para obter uma definição detalhada).

2. Um “circuito” é um subgrafo computacional de uma rede neural. Ele consiste em um conjunto de características e nas bordas ponderadas que passam entre eles na rede original. Geralmente, estudamos circuitos bem pequenos, por exemplo, com menos de uma dúzia de características, mas eles também podem ser muito maiores. (Consulte o glossário para obter uma definição detalhada).

3. A discordância da comunidade com relação a características significativas é difícil de ser definida e está apenas parcialmente expressa na literatura. As descrições fundamentais do aprendizado profundo geralmente descrevem as redes neurais como detectando uma hierarquia de características significativas [25], e vários artigos foram escritos demonstrando características aparentemente significativas em diferentes domínios [15, 2, 16, 17, 4, 18]. Ao mesmo tempo, desenvolveu-se uma literatura paralela mais cética, sugerindo que as redes neurais se concentram principalmente ou apenas na textura, na estrutura local ou em padrões imperceptíveis [20, 21, 22, 23], que características significativas, quando existem, são menos importantes do que as ininterpretáveis [24] e que neurônios aparentemente interpretáveis podem ser entendidos erroneamente [19]. Embora muitos desses artigos expressem uma visão altamente nuançada, nem sempre é assim que eles foram compreendidos. Vários artigos da mídia foram escritos abraçando versões fortes dessas opiniões, e, anedoticamente, descobrimos que a crença de que redes neurais não entendem nada além de textura é bastante comum. Por fim, as pessoas frequentemente têm dificuldade em articular suas opiniões exatas, porque não têm uma linguagem clara para articular nuances entre “um detector de textura altamente correlacionado com um objeto” e “um detector de objeto”.

4. Por que os neurônios polissemânticos são tão desafiadores? Se um neurônio com cinco significados diferentes se conecta a outro neurônio com cinco significados diferentes, são efetivamente 25 conexões que não podem ser consideradas individualmente.

5. muitos dos neurônios discutidos neste artigo, inclusive os detectores de curvas, vivem em ramos do InceptionV1 que são estruturados como uma convolução 1×1 que reduz o número de canais a um pequeno gargalo seguido por uma convolução 3×3 ou 5×5. Os pesos que apresentamos neste ensaio são a versão multiplicada dos pesos da convolução 1×1 e maior. Acreditamos que muitas vezes é útil visualizar isso como uma única matriz de peso de baixa classificação, mas isso tecnicamente ignora uma não linearidade de ReLU.

6. Para deixar claro, há também caminhos mais diretos pelos quais vários constituintes das cabeças influenciam esses detectores de cabeça posteriores, sem passar pelos caminhos da esquerda e da direita.

7. Fundamentalmente, essa é uma propriedade da geometria de espaços de alta dimensão, que só permitem n vetores ortogonais, mas exponencialmente muitos vetores quase ortogonais.

8. Uma possibilidade particularmente interessante seria se as redes neurais artificiais pudessem prever características até então desconhecidas, mas que pudessem ser encontradas na biologia. (Alguns neurocientistas com quem conversamos sugeriram que os detectores de alta-baixa frequência poderiam ser um candidato a isso). Se essa previsão pudesse ser feita, seria uma evidência extremamente forte da hipótese da universalidade.

9. Fomos apresentados ao trabalho de Kuhn e a essa conexão por meio de conversas com Tom McGrath na DeepMind.

10. Para ser claros, vemos pesquisadores que adotam mais essa abordagem de ciência natural, especialmente em pesquisas anteriores sobre interpretabilidade. Isso parece menos comum no momento.

Referências

1. Micrographia: or Some Physiological Descriptions of Minute Bodies Made by Magnifying Glasses. With Observations and Inquiries Thereupon  [link]
   Hooke, R., 1666. The Royal Society. DOI: 10.5962/bhl.title.904
2. Visualizing and understanding recurrent networks  [PDF]
   Karpathy, A., Johnson, J. and Fei-Fei, L., 2015. arXiv preprint arXiv:1506.02078.
3. Visualizing higher-layer features of a deep network  [PDF]
   Erhan, D., Bengio, Y., Courville, A. and Vincent, P., 2009. University of Montreal, Vol 1341, pp. 3.
4. Feature Visualization  [link]
   Olah, C., Mordvintsev, A. and Schubert, L., 2017. Distill. DOI: 10.23915/distill.00007
5. Deep inside convolutional networks: Visualising image classification models and saliency maps  [PDF]
   Simonyan, K., Vedaldi, A. and Zisserman, A., 2013. arXiv preprint arXiv:1312.6034.
6. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images  [PDF]
   Nguyen, A., Yosinski, J. and Clune, J., 2015. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 427–436. DOI: 10.1109/cvpr.2015.7298640
7. Inceptionism: Going deeper into neural networks  [HTML]
   Mordvintsev, A., Olah, C. and Tyka, M., 2015. Google Research Blog.
8. Plug & play generative networks: Conditional iterative generation of images in latent space  [PDF]
   Nguyen, A., Clune, J., Bengio, Y., Dosovitskiy, A. and Yosinski, J., 2016. arXiv preprint arXiv:1612.00005.
9. Visualizing and understanding convolutional networks  [PDF]
   Zeiler, M.D. and Fergus, R., 2014. European conference on computer vision, pp. 818–833.
10. Interpretable Explanations of Black Boxes by Meaningful Perturbation  [PDF]
    Fong, R. and Vedaldi, A., 2017. arXiv preprint arXiv:1704.03296.
11. PatternNet and PatternLRP–Improving the interpretability of neural networks  [PDF]
    Kindermans, P., Schutt, K.T., Alber, M., Muller, K. and Dahne, S., 2017. arXiv preprint arXiv:1705.05598. DOI: 10.1007/978-3-319-10590-1_53
12. Visualizing and Measuring the Geometry of BERT  [PDF]
    Reif, E., Yuan, A., Wattenberg, M., Viegas, F.B., Coenen, A., Pearce, A. and Kim, B., 2019. Advances in Neural Information Processing Systems, pp. 8592–8600.
13. Activation atlas  [link]
    Carter, S., Armstrong, Z., Schubert, L., Johnson, I. and Olah, C., 2019. Distill, Vol 4(3), pp. e15. DOI: 10.23915/distill.00015
14. Summit: Scaling Deep Learning Interpretability by Visualizing Activation and Attribution Summarizations  [PDF]
    Hohman, F., Park, H., Robinson, C. and Chau, D.H.P., 2019. IEEE Transactions on Visualization and Computer Graphics, Vol 26(1), pp. 1096–1106. IEEE.
15. Distributed representations of words and phrases and their compositionality  [PDF]
    Mikolov, T., Sutskever, I., Chen, K., Corrado, G.S. and Dean, J., 2013. Advances in neural information processing systems, pp. 3111–3119.
16. Learning to generate reviews and discovering sentiment  [PDF]
    Radford, A., Jozefowicz, R. and Sutskever, I., 2017. arXiv preprint arXiv:1704.01444.
17. Object detectors emerge in deep scene cnns  [PDF]
    Zhou, B., Khosla, A., Lapedriza, A., Oliva, A. and Torralba, A., 2014. arXiv preprint arXiv:1412.6856.
18. Network Dissection: Quantifying Interpretability of Deep Visual Representations  [PDF]
    Bau, D., Zhou, B., Khosla, A., Oliva, A. and Torralba, A., 2017. Computer Vision and Pattern Recognition.
19. On Interpretability and Feature Representations: An Analysis of the Sentiment Neuron
    Donnelly, J. and Roegiest, A., 2019. European Conference on Information Retrieval, pp. 795–802.
20. Measuring the tendency of CNNs to Learn Surface Statistical Regularities  [PDF]
    Jo, J. and Bengio, Y., 2017. arXiv preprint arXiv:1711.11561.
21. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness  [PDF]
    Geirhos, R., Rubisch, P., Michaelis, C., Bethge, M., Wichmann, F.A. and Brendel, W., 2018. arXiv preprint arXiv:1811.12231.
22. Approximating cnns with bag-of-local-features models works surprisingly well on imagenet  [PDF]
    Brendel, W. and Bethge, M., 2019. arXiv preprint arXiv:1904.00760.
23. Adversarial examples are not bugs, they are features  [PDF]
    Ilyas, A., Santurkar, S., Tsipras, D., Engstrom, L., Tran, B. and Madry, A., 2019. Advances in Neural Information Processing Systems, pp. 125–136.
24. On the importance of single directions for generalization  [PDF]
    Morcos, A.S., Barrett, D.G., Rabinowitz, N.C. and Botvinick, M., 2018. arXiv preprint arXiv:1803.06959.
25. Deep learning  [PDF]
    LeCun, Y., Bengio, Y. and Hinton, G., 2015. nature, Vol 521(7553), pp. 436–444. Nature Publishing Group.
26. Going deeper with convolutions  [PDF]
    Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., Rabinovich, A. and others,, 2015. DOI: 10.1109/cvpr.2015.7298594
27. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex
    Hubel, D.H. and Wiesel, T.N., 1962. The Journal of physiology, Vol 160(1), pp. 106–154. Wiley Online Library.
28. Using Artificial Intelligence to Augment Human Intelligence  [link]
    Carter, S. and Nielsen, M., 2017. Distill. DOI: 10.23915/distill.00009
29. Multifaceted feature visualization: Uncovering the different types of features learned by each neuron in deep neural networks  [PDF]
    Nguyen, A., Yosinski, J. and Clune, J., 2016. arXiv preprint arXiv:1602.03616.
30. An introduction to systems biology: design principles of biological circuits
    Alon, U., 2019. CRC press. DOI: 10.1201/9781420011432
31. Convergent learning: Do different neural networks learn the same representations?  [PDF]
    Li, Y., Yosinski, J., Clune, J., Lipson, H. and Hopcroft, J.E., 2015. FE@ NIPS, pp. 196–212.
32. SVCCA: Singular Vector Canonical Correlation Analysis for Deep Learning Dynamics and Interpretability  [PDF]
    Raghu, M., Gilmer, J., Yosinski, J. and Sohl-Dickstein, J., 2017. Advances in Neural Information Processing Systems 30, pp. 6078–6087. Curran Associates, Inc.
33. Similarity of neural network representations revisited  [PDF]
    Kornblith, S., Norouzi, M., Lee, H. and Hinton, G., 2019. arXiv preprint arXiv:1905.00414.
34. ImageNet Classification with Deep Convolutional Neural Networks  [PDF]
    Krizhevsky, A., Sutskever, I. and Hinton, G.E., 2012. Advances in Neural Information Processing Systems 25, pp. 1097–1105. Curran Associates, Inc.
35. Very Deep Convolutional Networks for Large-Scale Image Recognition  [PDF]
    Simonyan, K. and Zisserman, A., 2014. CoRR, Vol abs/1409.1556.
36. Deep Residual Learning for Image Recognition  [PDF]
    He, K., Zhang, X., Ren, S. and Sun, J., 2015. CoRR, Vol abs/1512.03385.
37. Performance-optimized hierarchical models predict neural responses in higher visual cortex
    Yamins, D.L., Hong, H., Cadieu, C.F., Solomon, E.A., Seibert, D. and DiCarlo, J.J., 2014. Proceedings of the National Academy of Sciences, Vol 111(23), pp. 8619–8624. National Acad Sciences.
38. Deep neural networks reveal a gradient in the complexity of neural representations across the ventral stream
    Gu{\c{c}}lu, U. and van Gerven, M.A., 2015. Journal of Neuroscience, Vol 35(27), pp. 10005–10014. Soc Neuroscience.
39. Seeing it all: Convolutional network layers map the function of the human visual system
    Eickenberg, M., Gramfort, A., Varoquaux, G. and Thirion, B., 2017. NeuroImage, Vol 152, pp. 184–194. Elsevier.
40. Discrete neural clusters encode orientation, curvature and corners in macaque V4  [link]
    Jiang, R., Li, M. and Tang, S., 2019. bioRxiv. Cold Spring Harbor Laboratory. DOI: 10.1101/808907
41. Shape representation in area V4: position-specific tuning for boundary conformation
    Pasupathy, A. and Connor, C.E., 2001. Journal of neurophysiology, Vol 86(5), pp. 2505–2519. American Physiological Society Bethesda, MD.
42. The structure of scientific revolutions
    Kuhn, T.S., 1962. University of Chicago press. DOI: 10.7208/chicago/9780226458106.001.0001
43. Ian Goodfellow: Generative Adversarial Networks  [link]
    Goodfellow, I. and Fridman, L., 2019. Artificial Intelligence Podcast.
44. The Building Blocks of Interpretability  [link]
    Olah, C., Satyanarayan, A., Johnson, I., Carter, S., Schubert, L., Ye, K. and Mordvintsev, A., 2018. Distill. DOI: 10.23915/distill.00010

Atualizações e Correções

Se vir erros ou quiser sugerir modificações, por favor, crie uma edição no GitHub.

Reuso

Diagramas e textos estão licenciados sob Creative Commons Attribution CC-BY 4.0 com a fonte disponível no GitHub, a menos que observado de outra forma. As figuras que foram reutilizadas de outras fontes não estão sob essa licença e podem ser reconhecidas por uma nota em sua legenda: “Figura de …”.

---

Tradução: Luan Marques

Link para o original