Blog

Resumo

Historicamente, o progresso no campo da criptografia tem sido extremamente importante. Ao longo do século passado, por exemplo, as descobertas criptográficas desempenharam um papel fundamental em uma guerra mundial e possibilitaram o uso da internet para negócios e comunicações privadas. No interesse de explorar o impacto que o campo pode ter no futuro, considero um conjunto de desenvolvimentos mais recentes. Meu foco principal está em tecnologias baseadas em blockchain (como criptomoedas) e em técnicas de computação de dados confidenciais (como computação segura de várias partes). Forneço uma introdução a essas tecnologias que não pressupõe nenhuma base matemática ou conhecimento prévio de criptografia. Em seguida, considero várias previsões especulativas que alguns pesquisadores e engenheiros fizeram sobre o significado político de longo prazo das tecnologias. Isso inclui previsões de que mais formas de vigilância “que preservam a privacidade” se tornarão possíveis, que os papéis de instituições centralizadas, desde bancos até autoridades eleitorais, diminuirão e que novas instituições transnacionais conhecidas como “organizações autônomas descentralizadas” surgirão. Por fim, encerro discutindo alguns desafios que provavelmente limitarão a importância das tecnologias criptográficas emergentes. Com base nesses desafios, é prematuro prever que algum deles se aproximará da capacidade de transformação das tecnologias anteriores. No entanto, esta continua a ser uma área em rápido desenvolvimento que vale a pena seguir.

1. Introdução

O século passado viu o surgimento de várias tecnologias transformadoras, desde armas nucleares até computadores.

Para antecipar desafios e oportunidades futuros, vale a pena considerar quais áreas da tecnologia, se houver, poderiam desempenhar papéis igualmente importantes neste século. Uma área que recentemente provocou grande entusiasmo é a criptografia, ou o estudo de técnicas para codificar, proteger e autenticar dados.

Indiscutivelmente, o progresso na criptografia (e seu campo complementar, a criptoanálise, que se concentra na decodificação) já deveria ser incluído em qualquer lista dos desenvolvimentos mais importantes do século passado [13]. O caso mais famoso de criptografia e criptoanálise no século XX pode ser o uso da criptografia avançada pela Alemanha durante a Segunda Guerra Mundial e o correspondente esforço de criptoanálise da Grã-Bretanha, que pelo menos um historiador estimou que acelerou a vitória dos Aliados em mais de um ano [94]. Mais recentemente, tecnologias criptográficas desenvolvidas nos últimos cinquenta anos permitiram que a internet (e outros canais de comunicação de longa distância) fosse usada para propósitos que seriam impraticáveis sem elas, como fazer transações financeiras e enviar mensagens privadas. Além disso, o uso bem-sucedido da criptografia representa um desafio contínuo para os programas governamentais de vigilância e inteligência.

Na última década, várias novas tecnologias criptográficas começaram a surgir (consulte a Tabelas 1). Essas tecnologias incluem blockchains, que permitiram a criação de registros altamente confiáveis e aplicativos de computador que nenhuma parte única controla; criptomoedas, como a bitcoin, que acumularam centenas de bilhões de dólares em valor e permitem que os usuários façam transações digitais sem depender de instituições financeiras tradicionais ou moedas fiduciárias tradicionais; contratos inteligentes, que permitem aos usuários entrar em acordos que são aplicados em grande parte por algoritmos; e criptografia totalmente homomórfica, que permite aos usuários processar dados sem ter acesso a eles de forma não criptografada². Algumas tecnologias existentes, como computação segura de várias partes, também se tornaram muito mais práticas de implementar ou encontraram novas aplicações.

Resta saber se esses desenvolvimentos recentes na criptografia serão tão significativos quanto os anteriores. No entanto, várias afirmações bastante radicais foram feitas sobre sua importância. Listo apenas alguns exemplos: o Escritório de Ciência do Governo do Reino Unido descreveu blockchains como a primeira inovação significativa na manutenção de registros desde os tempos antigos [179]. Ralph Merkle, uma das figuras fundadoras da criptografia moderna, escreveu um artigo argumentando que blockchains permitirão novas formas de democracia [113]. Jaan Tallinn, cofundador do Skype e do Future of Life Institute, defendeu o uso da tecnologia de contrato inteligente para resolver problemas globais de ação coletiva [35]. Em outros lugares, pesquisadores argumentaram que as criptomoedas poderiam tornar muito mais difícil para os governos influenciar ou rastrear transações privadas, enquanto outros escreveram que a criptografia homomórfica poderia permitir novas formas de vigilância que exigem menos violação da privacidade dos indivíduos [83, 166].

Infelizmente, as discussões sobre tais reivindicações muitas vezes se desenrolam em postagens de blog e artigos dispersos que é difícil para um leitor não especializado encontrar ou entender. Este relatório pretende ser uma contribuição ao projeto de recolher e esclarecer essas discussões.

Em particular, este relatório está dividido em três seções: primeiro, apresento alguns desenvolvimentos recentes na criptografia, com o objetivo de incluir o nível mínimo de detalhes necessário para discutir claramente sobre as tecnologias relevantes. Em segundo lugar, descrevo várias consequências politicamente significativas e de longo prazo. Por fim, exploro algumas das limitações técnicas e restrições políticas que poderiam impedir o surgimento dessas consequências.

Além disso, um apêndice discute sobre a relação entre o futuro da criptografia e o futuro da inteligência artificial.

Para leitores que ainda não estão familiarizados com criptografia, é melhor que se leia a primeira seção em ordem. No entanto, as subseções posteriores não são tão dependentes umas das outras.

2 Tecnologias criptográficas: definições, explicações e exemplos

O conjunto de tecnologias criptográficas que iremos considerar é altamente diversificado. De interesse neste relatório serão:

• Criptografia de chave pública
• Assinaturas digitais
• Funções hash criptográficas
• Carimbo de temporal confiável
• Registros invioláveis
• Blockchains
• Criptomoedas
• Provas de conhecimento zero
• Propriedade inteligente
• Contratos inteligentes
• Criptografia homomórfica
• Criptografia funcional
• Computação segura de várias partes e compartilhamento secreto

Algumas dessas tecnologias são novas, tendo sido desenvolvidas principalmente nos últimos quinze anos. Algumas são mais antigas, mas servem como componentes centrais dessas tecnologias mais recentes ou continuam a encontrar aplicações adicionais próprias. Nesta seção, pretendo fornecer descrições de cada tecnologia que sejam suficientes para permitir discussões informadas sobre suas possíveis aplicações e limitações.

Para uma visão geral, a Tabelas 1 fornece um resumo altamente abreviado. Além disso, para uma análise mais profunda, também recomendarei algumas fontes para leitura posterior.

Leitores interessados em descrições mais completas ou técnicas de tecnologias bem estabelecidas, como criptografia de chave pública, assinaturas digitais e funções hash criptográficas, podem encontrá-las em qualquer um dos vários livros introdutórios amplamente usados, como Introduction to Modern Cryptography de Jonathan Katz e Yehuda Lindell [99].

Leitores interessados em blockchains, criptomoedas, propriedade inteligente e contratos inteligentes podem encontrar discussões sobre eles no livro Bitcoin and Cryptocurrency Technologies de Narayanan et al. [119]. O livro branco de Vitalik Buterin para a blockchain Ethereum e a tese de Ethan Buchman que descreve a blockchain Tendermint também continuam a servir como boas introduções à própria tecnologia blockchain [41, 34]. Muitas das postagens do blog de Vitalik Buterin também fornecem descrições inusitadamente lúcidas de diferentes aspectos do ecossistema da blockchain [38, 39].

Provas de conhecimento zero e computação segura de várias partes recebem cobertura em muitos livros-texto de criptografia intermediários. Há um punhado de tratamentos extensos. Para uma introdução às provas de conhecimento zero com foco em desenvolvimentos recentes, recomendo a série “Explainings SNARKs” no blog de Zcash [186]. Para uma introdução acessível à computação segura de várias partes, recomendo o artigo “Secure Multiparty Computation for Privacy-Preservation Data Mining” de Lindell e Pinkas [108]. Além disso, “Computing Blindfolded: New Developments in Fully Homomorphic Encryption” [171] de Vaikun Tanathan e “Functional Encryption: Definitions and Challenges” [27] de Boneh et al. são introduções razoáveis à criptografia homomórfica e à criptografia funcional, respectivamente.

Por fim, é importante observar que a lista de tecnologias que escolhi investigar não é completa. Entre as áreas que excluí, a mais importante pode ser o subcampo da criptografia quântica, que aplica fenômenos quânticos a tarefas criptográficas. Essa exclusão é principalmente uma questão de espaço limitado, embora também seja importante notar que muitas das tecnologias mais interessantes associadas à criptografia quântica (como dinheiro quântico e proteção quântica contra cópia) se destacam como particularmente distantes de aplicações práticas [1]. Outras tecnologias potencialmente significativas, não discutidas neste relatório, incluem ofuscação de programas e computação verificável. A ofuscação de programas permite que os usuários compartilhem programas de computador com outros enquanto deixam seu funcionamento interno opaco, e a computação verificável permite que os usuários terceirizem cálculos para outros e recebam provas curtas de que os cálculos foram executados conforme o prometido [139, 178]. Ambas as tecnologias também estão associadas a uma série de avanços na última década.

Tecnologia	Origem	Descrição Funcional
Criptografia de chave pública	1973	Permite que os usuários se comuniquem por meio de código sem compartilhar informações secretas com antecedência
Assinaturas digitais	1979	Permite que os usuários identifiquem os remetentes das mensagens
Funções hash criptográficas	1979	Permite que os usuários associem dados a “impressões digitais” exclusivas
Carimbo temporal confiável	1991	Permite que os usuários marquem partes de dados com relação ao tempo
Registros invioláveis	1979 (ambíguo)	Contêm registros cronológicos que não podem ser editados discretamente
Máquinas de estado replicadas	1984	Replica o fornecimento de um serviço em vários computadores
Blockchains	2008	Máquinas de estado replicadas que mantêm registros invioláveis
Blockchains sem permissão	2008	Blockchains que permitem que qualquer computador participe da prestação de serviços
Aplicativos descentralizados	1980 (ambíguo)	Aplicativos associados a um conjunto aberto de provedores de serviços (como em uma blockchain sem permissão)
Blockchains de consórcio	2012 (ambíguo)	Blockchains que permitem que computadores pertencentes a várias partes (mas não qualquer computador) participem da prestação de serviços
Aplicativos sustentados por consórcio	Ambíguo	Aplicativos associados a vários provedores de serviços privilegiados (como em uma blockchain de consórcio)
Criptomoedas	2008	Moedas digitais cuja propriedade é gerenciada por meio de um aplicativo descentralizado ou sustentado por consórcio; também são essenciais para a operação de blockchains sem permissão
Provas de conhecimento zero	1985	Permite que os usuários provem declarações matemáticas para outras pessoas sem transmitir informações adicionais
zk-SNARKs	2010	Permite que os usuários façam o que foi dito acima de forma sucinta e sem interações de ida e volta
Provas físicas de conhecimento zero	2012 (ambíguo)	Permite que os usuários provem declarações sobre objetos físicos para outras pessoas sem transmitir informações adicionais
Propriedade inteligente	1994	Dispositivos com componentes eletrônicos que facilitam essa transferência da sua propriedade
Contratos inteligentes	1994	Contratos cuja execução é significativamente automatizada
Criptografia homomórfica	1973	Permite que os usuários executem determinados cálculos em dados criptografados; as saídas também são criptografadas
Criptografia totalmente homomórfica	2009	Permite que os usuários executem quaisquer cálculos em dados criptografados; as saídas também são criptografadas
Criptografia funcional	2010	Permite que os usuários executem certos cálculos em dados criptografados, de modo que as saídas não sejam criptografadas
Computação segura de várias partes	1982	Permite que os usuários executem cálculos com entradas de várias partes, permitindo que essas partes mantenham suas próprias entradas em segredo
Compartilhamento secreto	1979	Permite que os usuários dividam dados privados em compartilhamentos, que podem ser recombinados para recuperar os dados

2.1 Criptografia de chave pública

A encriptação de chave pública é uma tecnologia que permite aos usuários se comunicarem por meio de código sem compartilhar informações secretas antecipadamente [57, 99].

Digamos que uma das partes, Alice, queira enviar uma mensagem privada para outra parte, Beto, usando um canal que pode ter bisbilhoteiros. Por exemplo, Alice pode querer compartilhar um segredo com Beto por e-mail sem que mais ninguém — como uma agência de inteligência do governo — seja capaz de descobrir o segredo também. A maneira de fazer isso é criptografar a mensagem, ou seja, codificá-la de uma forma que ninguém mais possa entender.

A classe mais antiga de esquemas de criptografia, conhecida como esquemas de chave simétrica, é usada há milhares de anos. Esses esquemas dependem de uma única informação compartilhada, conhecida como chave secreta, e uma regra mutuamente compreendida para traduzir mensagens não criptografadas (ou texto simples) e mensagens criptografadas (ou texto cifrado) entre si usando essa chave. Por exemplo, na simples “cifra de César”, a chave era um número curto, X, e a regra para traduzir texto simples em texto cifrado era mover cada letra individual para frente em X casas no alfabeto³.

O problema com os esquemas de chave simétrica é que, para ser usado, ambas as partes devem, de alguma forma, estabelecer uma chave secreta sem que terceiros também a conheçam. No entanto, a dificuldade de comunicar informações secretas como essa é exatamente a dificuldade que a criptografia pretende resolver em primeiro lugar. Os esquemas de criptografia de chave privada, portanto, sofrem de um problema de “ovo e galinha”. O problema é ainda agravado pelo fato de que as chaves secretas não podem ser reutilizadas sem uma perda de segurança muito significativa.

A criptografia de chave pública, desenvolvida pela primeira vez na década de 1970, resolve esse problema. Em um esquema de chave pública, não há uma única chave. Em vez disso, cada pessoa em uma rede possui um par exclusivo de chaves: uma conhecida como chave privada e outra conhecida como chave pública. Embora os detalhes técnicos não precisem nos preocupar, estas são as características que definem um sistema de chave pública:

• Existe um algoritmo de configuração que cada parte do sistema pode usar para gerar um par de chaves (quase certamente) exclusivo.
• Cada parte do sistema pode anunciar sua chave pública sem revelar sua chave privada. As chaves públicas também podem ser usadas como pseudônimos digitais.
• Existe um algoritmo de encriptação que pode receber uma mensagem de texto simples e a chave pública do destinatário como entradas e, em seguida, produzir uma mensagem codificada como saída. Há também um algoritmo de desencriptação que pode pegar uma mensagem codificada e a chave privada do destinatário e, em seguida, produzir a mensagem original como saída. Aplicando esses dois algoritmos em sequência, o remetente e o destinatário podem se comunicar por meio de código⁴.
• Não há algoritmo prático que permita a qualquer pessoa sem a chave privada do destinatário decodificar a mensagem do remetente.

Conforme declarado acima, a criptografia de chave pública não é uma tecnologia nova. Após seu desenvolvimento inicial (ou, mais precisamente, redescoberta por acadêmicos fora da comunidade de pesquisa confidencial), a possibilidade de sua ampla adoção foi por muitos anos considerada uma ameaça por agências governamentais como, nos Estados Unidos, a NSA e a o FBI [11]. Essas agências argumentaram que, sem a capacidade de ler as mensagens interceptadas, seriam muito menos capazes de combater atividades criminosas e outras ameaças à segurança. Eles buscaram várias estratégias para retardar a adoção da tecnologia ou proibir variantes que não concedessem ao governo uma “porta dos fundos” para decifrar mensagens usando suas próprias chaves privadas especiais.

Por fim, ficou claro no final da década de 1990 que essas agências haviam perdido a luta e, pelo menos nos Estados Unidos e na União Européia, o uso de todas as formas de criptografia de chave pública agora é perfeitamente legal [140]. Até recentemente, porém, a grande maioria dos serviços de mensagens ainda aplicava criptografia de forma a permitir que o provedor de serviços e, portanto, as agências governamentais acessassem as mensagens não criptografadas de seus usuários. Parcialmente como reação aos vazamentos de Snowden em 2013, esse estado de espírito começou a mudar. Tornou-se cada vez mais comum que os serviços ofereçam criptografia de ponta a ponta, que, na prática, refere-se a implementações de mensagens criptografadas que não concedem privilégios de visualização aos provedores de serviços [59]. Ao longo de apenas o ano de 2016, o número de usuários de criptografia de ponta a ponta em todos os serviços pode ter aumentado em mais de um bilhão, em grande parte devido à decisão do WhatsApp de começar a habilitar o recurso por padrão [12]. Além disso, vários grupos estão trabalhando para desenvolver serviços práticos de mensagens de ponta a ponta que também podem ocultar de forma confiável os metadados de cada mensagem, como seu destinatário [172]. Se esses projetos forem bem-sucedidos, a privacidade do usuário pode aumentar ainda mais.

Embora até mesmo o uso de criptografia de ponta a ponta perfeitamente implementada não garanta que as mensagens de alguém não sejam lidas por ninguém além do destinatário pretendido, ela diminui as chances de bisbilhotagem bem-sucedida⁵. Agências em vários países agora alegam, controversamente, que os canais de informação nos quais eles confiam estão cada vez mais “se escurecendo” [70].

2.2 Assinaturas digitais

Uma assinatura digital pode ser usada para demonstrar que um determinado dado foi enviado pelo proprietário de um determinado par de chaves (ver seção 2.1) e que não foi modificado desde o seu envio [136, 99].

As assinaturas digitais funcionam da seguinte maneira:

• Cada parte do sistema concorda com um algoritmo de assinatura e um algoritmo de verificação de assinatura.
• O algoritmo de assinatura pega e um dado a chave privada de uma parte e gera um código conhecido como uma assinatura.
• O algoritmo de verificação de assinatura pega um dado e uma assinatura e a chave pública de uma parte e gera “Sim” como saída se e somente se a assinatura foi gerada a partir dos dados e da chave privada correspondente⁶.

Atualmente, o uso de assinaturas digitais é onipresente on-line e, entre muitas outras aplicações, permite o comércio on-line. Por exemplo, quando você faz compras on-line, seu computador verifica se você está de fato conectado à Amazon.com (e não a um golpista em busca dos detalhes do seu cartão de crédito), verificando uma assinatura enviada por uma chave pública que sabe-se que está associada ao site.

Nos últimos anos, alguns países também passaram a atribuir chaves públicas a seus cidadãos como uma forma de identificação, para que os indivíduos possam provar suas identidades, acessar registros governamentais pessoalmente relevantes, votar e até mesmo assinar contratos juridicamente vinculativos usando assinaturas digitais (normalmente armazenadas em cartões de identificação altamente protegidos) [110]. A Estônia é o caso mais notável, com seus cidadãos tendo emitido centenas de milhões de assinaturas desde o início do programa.

2.3 Funções hash criptográficas

Uma função hash criptográfica codifica um dado como um código de certa extensão fixa, conhecido como um hash (ou resumo) [114, 99]. A função tem as seguintes propriedades:

• É fácil verificar se um determinado dado produz um determinado hash.
• Dados que são apenas ligeiramente diferentes produzirão hashes muito diferentes.
• É impraticável encontrar um dado que produza um determinado hash, ou encontrar dois dados que produzam hashes idênticos.

De certa forma, os hashes agem como “impressões digitais” para dados. Da mesma forma que cada ser humano está associado a um conjunto quase certamente único de impressões digitais, sem que essas impressões digitais forneçam alguma outra informação sobre a pessoa, cada dado pode ser associado a um hash quase certamente único, sem que esse hash forneça alguma outra informação sobre os dados.

Indiscutivelmente, as funções hash são importantes principalmente como um bloco de construção para outras tecnologias criptográficas. Discutiremos agora um trio dessas tecnologias: carimbo temporal confiável, registros invioláveis e blockchains.

2.4 Carimbo temporal confiável

Uma área de aplicação interessante para funções hash criptográficas é o carimbo temporal confiável, ou técnicas para demonstrar que um determinado dado existiu em um determinado momento [84, 170]. Em muitos casos, a tarefa é significativamente complicada pelo desejo do usuário de manter os dados privados no momento do seu carimbamento temporal.

Por exemplo, suponha que você tenha algum resultado de pesquisa que não está pronto para publicar, mas pelo qual gostaria de reivindicar prioridade. Uma solução simples é pegar o hash de seus dados e publicá-lo em um jornal ou site em que se possa confiar para registrar os tempos de publicação de maneira confiável. Mais tarde, você pode publicar os resultados reais da pesquisa e, comparando seu hash com o hash publicado, as pessoas poderão verificar por si mesmas que você tinha os resultados no momento da publicação do hash.

Como exemplo dessa técnica, a organização política WikiLeaks às vezes publica hashes de documentos confidenciais que obtém no Twitter [158]. Se os hashes de documentos que acabam sendo liberados não corresponderem — como aconteceu em pelo menos um caso —, ficará claro que alguém modificou os documentos desde que o WikiLeaks anunciou sua existência⁷.

Outros casos de uso para o carimbo temporal confiável incluem a prevenção da falsificação de documentos e mídia digital. Muitas vezes, o fato de um dado ser anterior a um determinado ponto no tempo pode fornecer evidências de que ele é genuíno. Os investigadores podem confiar que um documento do governo com carimbo temporal, por exemplo, não foi inventado após o ocorrido para encobrir os rastros de um funcionário corrupto. Da mesma forma, se uma fotografia alega retratar uma reunião secreta entre dois funcionários em um determinado dia, será muito mais confiável se realmente tiver o carimbo temporal daquele dia. Conforme discutido na seção 3.1.4, este último caso de uso pode se tornar muito mais importante à medida que a inteligência artificial se torna cada vez mais eficiente e eficaz na falsificação de fotografias e vídeos [4].

Como ponto técnico final, às vezes pode ser útil associar uma grande coleção de dados a um único carimbo temporal. Ingenuamente, uma maneira simples de realizar essa tarefa é aplicar uma função hash à coleção completa em conjunto. No entanto, este método tem uma desvantagem significativa. Em particular, usando esse método, é impossível demonstrar que um único dado da coleção foi usado para produzir o carimbo temporal sem também compartilhar o restante da coleção, o que pode ser indesejável do ponto de vista da eficiência ou da privacidade.

Um método melhor de carimbar temporalmente uma grande coleção de dados de uma só vez é usar árvores de Merkle (consulte a Figura 1). Árvores de Merkle são produzidas aplicando uma função hash a cada dado individualmente, e daí repetidamente aplicando funções hash a pares de hashes para formar uma estrutura de árvore. O hash que fica no topo da árvore resultante é conhecido como a raiz de Merkle. A raiz de Merkle, se publicada, serve igualmente bem como uma “impressão digital” para toda a coleção. Mas, se alguém quiser provar que um dado em particular pertence à coleção carimbada temporalmente, é necessário apenas compartilhar esse dado em particular e uma porção relativamente pequena da árvore de Merkle, em vez de ser necessário compartilhar os outros dados também.

As árvores de Merkle foram propostas pela primeira vez no final dos anos 1970, por Ralph Merkle, e talvez tenham sido usadas com mais frequência no contexto de serviços de hospedagem e compartilhamento de arquivos que desejam garantir aos usuários que os arquivos não foram alterados em suas versões mais recentes.

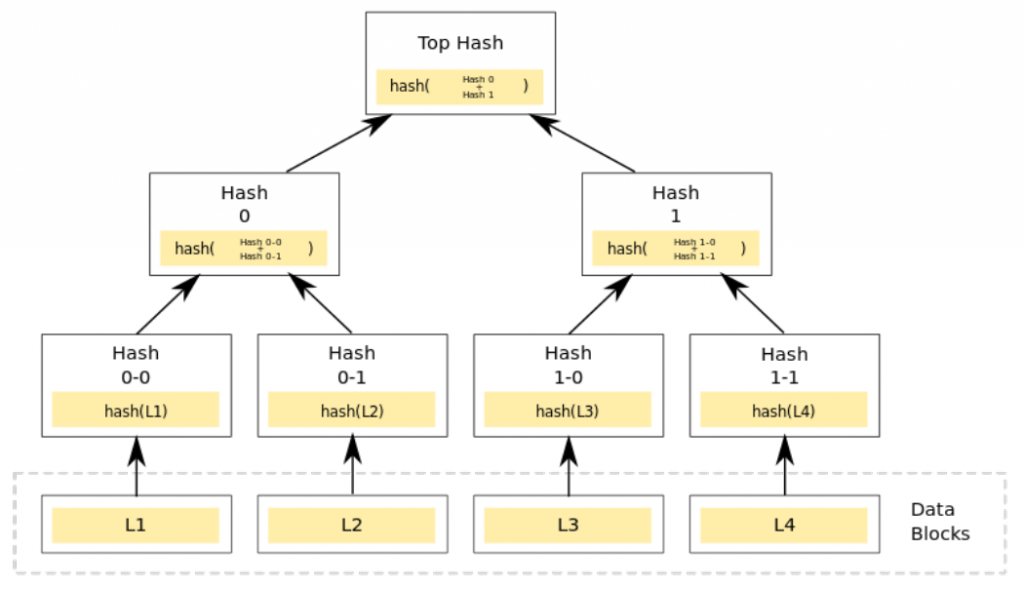
Figura 1: uma árvore de Merkle. O hash superior, ou a raiz de Merkle, serve como uma “impressão digital” para os blocos de dados na parte inferior. Aqui, provar que o bloco de dados L1 é consistente com a raiz Merkle exigiria o compartilhamento apenas do próprio bloco e dos dois hashes Hash0-1 e Hash1. Não há necessidade de compartilhar os outros blocos de dados. (Imagem de David Gäthberg).

2.5 Registros invioláveis

Um registro inviolável é uma coleção cronológica de registros projetada para que quaisquer alterações nos registros, uma vez adicionadas, sejam facilmente detectáveis [55] ⁸.

Os registros invioláveis são uma tecnologia altamente valiosa, na medida em que a manutenção confiável de registros desempenha um papel crucial na vida política e econômica. Seria de esperar, por exemplo, que os registros bancários, médicos, fiscais, de propriedade e criminais continuassem a ser mantidos adequadamente.

Em muitos casos, as gravações em um registro são objetos de interesse significativo por si mesmos. Os registros geralmente são úteis instrumentalmente, permitindo que os usuários verifiquem a integridade de processos ou serviços mais sofisticados. Por exemplo, um registro confiável de depósitos, retiradas e transferências pode ser usado para determinar o saldo correto de uma conta bancária ou para restaurá-lo a um valor anterior se ocorrer um erro. Em geral, muitos aplicativos de computador estão associados a registros, geralmente chamados de registros de transações, que rastreiam como eles respondem aos inputs do usuário ao longo do tempo.

Conceder às partes que mantêm esses registros a capacidade de detectar mais facilmente tentativas de adulterá-los e demonstrar mais facilmente a terceiros que seus registros não foram adulterados pode ser um benefício significativo para a segurança e a confiança.

Um design se destaca como particularmente eficaz (consulte a Figura 2). Embora a terminologia adequada seja contestada, vou me referir a ela como um registro ligado por hashes. Aqui, o registro é subdividido em blocos sequenciais. Toda vez que um número suficiente de novas gravações é coletado, elas são reunidas em um novo bloco e adicionadas à sequência. Cada bloco é dividido em duas seções, uma que contém gravações e outra conhecida como cabeçalho. Por sua vez, cada cabeçalho contém a data, a raiz de Merkle dos registros que o bloco contém e o hash do cabeçalho anterior.

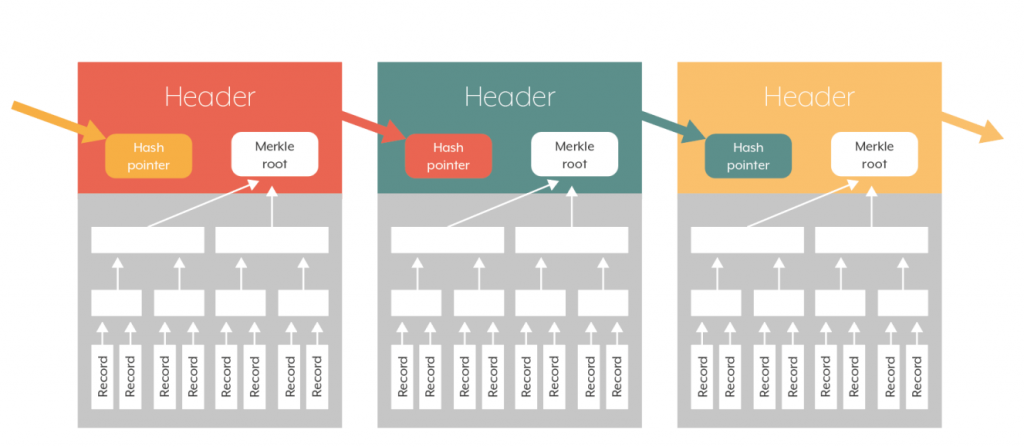
Suponha que Alice esteja mantendo tal registro — digamos, para um serviço de pagamento on-line que Beto usa — e que ela publique os cabeçalhos de blocos à medida que são criados. Ao incluir raízes de Merkle nos cabeçalhos, Alice carimba os registros de cada bloco quando ela publica seu cabeçalho. Ao incluir ponteiros de hashes nos cabeçalhos, porém, ela também vai além e estabelece uma sequência canônica de registros. Agora é impraticável, por exemplo, para Alice remover um bloco do registro sem produzir uma inconsistência com os cabeçalhos que o seguem; ela também não pode criar simultaneamente duas versões contraditórias de um bloco e, posteriormente, trocar discretamente uma pela outra⁹.

Geralmente, podemos entender os registros ligados por hashes como obtendo sua segurança por meio do uso de carimbos temporais ligados, uma classe de técnicas de carimbo temporal em que cada carimbo temporal faz referência ao anterior.

Embora o esquema de carimbos temporais ligados descrito aqui remonte a uma série de artigos de Haber e Stornetta no início dos anos 1990, vários governos e empresas recentemente se interessaram por suas aplicações. O objetivo é proteger a integridade de suas gravações e fornecer maiores garantias aos seus cidadãos ou clientes. O governo da Estônia, por exemplo, começou em 2008 a usar um serviço de carimbos temporais ligados para registrar alterações em alguns tipos de documentos governamentais. A empresa de pesquisa Google DeepMind também iniciou um projeto, em 2017, para desenvolver um sistema de registro inviolável para o uso do Serviço de Saúde Nacional Britânico [91].

2.11.Criptografia homomórfica

A criptografia homomórfica é uma forma de criptografia que permite que cálculos sejam executados em dados criptografados, de modo que as saídas dos cálculos também sejam criptografadas [171].

Por exemplo, dizemos que um esquema de criptografia é “homomórfico sob adição” se pudermos criptografar quaisquer dois números, executar uma determinada operação neles e, em seguida, descriptografar o resultado para retornar sua soma. Esquemas eficientes que são homomórficos apenas sob adição ou apenas sob multiplicação são conhecidos há vários anos³⁴.

Um esquema é conhecido como totalmente homomórfico se permite que qualquer função computável seja computada em dados criptografados. O primeiro esquema totalmente homomórfico foi inventado em 2009, por Craig Gentry [72]. Desde então, várias alternativas superiores também foram propostas.

O apelo básico da criptografia totalmente homomórfica é que ela possibilita a criação de aplicativos nos quais os provedores de serviços não exigem acesso aos dados não criptografados dos clientes. Possíveis exemplos incluem serviços de computação em nuvem que não precisam saber os dados que estão sendo solicitados a computar, serviços médicos on-line que sinalizam problemas de saúde com base no DNA de indivíduos sem a necessidade de conhecer seus dados genéticos e serviços de publicidade direcionados que não precisam saber os interesses que os usuários indicaram através de seu comportamento de navegação.

No entanto, a criptografia totalmente homomórfica ainda não encontrou uso significativo, pois todos os esquemas conhecidos são altamente ineficientes. Os esquemas mais eficientes descobertos até agora ainda resultam em explosões de muitas ordens de grandeza no tamanho dos dados criptografados à medida que são operados e no tempo que as operações levam para serem concluídas. Por exemplo, em 2014, mesmo uma implementação bem otimizada sendo executada em um computador moderadamente poderoso pode ser incapaz de realizar mais de 50 multiplicações por segundo (com a adição sendo muito menos dispendiosa) [8]. Na verdade, isso é uma grande melhoria em relação ao esquema original de Gentry, mas ainda extremamente lento. Numa aproximação muito grosseira, os dados totalmente criptografados homomorficamente podem ser considerados cerca de um bilhão de vezes menos eficientes de calcular do que os dados não criptografados.

Alguma ajuda é fornecida por esquemas de criptografia um tanto homomórficos, desenvolvidos simultaneamente, que oferecem acelerações significativas (mas não decisivas) às custas de permitir apenas um número finito de multiplicações. Com o tempo, mais progressos na descoberta de algoritmos eficientes e no desenvolvimento de computadores mais poderosos poderiam tornar a criptografia totalmente ou um tanto homomórfica prática em uma ampla gama de casos. No momento, no entanto, suas aplicações permanecem relativamente limitadas [117].

Nas duas seções a seguir, consideramos duas tecnologias adicionais que permitem que cálculos sejam executados em dados privados. Trata-se da criptografia funcional e da computação segura de várias partes.

Notas

2. Algumas dessas tecnologias, particularmente criptomoedas e contratos inteligentes, diferem das tecnologias criptográficas mais tradicionais de duas maneiras importantes. Primeiro, elas dependem em parte de sistemas de incentivos econômicos para funcionar e, segundo, suas aplicações dizem respeito principalmente à transferência de propriedade. Por essas razões, pode ser mais apropriado referir-se a elas como tecnologias “criptoeconômicas”, como fazem atualmente alguns engenheiros que trabalham para desenvolvê-las [154]. No entanto, como nenhuma terminologia-padrão foi adotada ainda, continuarei a usar o termo “criptografia” como um todo.

3. Como exemplo, a tecla “1” transformaria a mensagem “Olá” em “IFMMP”.

4. Para expressar isso matematicamente, seja Enc o algoritmo de criptografia, Dec o algoritmo de descriptografia, u a chave pública de um usuário, r a chave privada do mesmo usuário e m uma mensagem. Então, Enc(m,u) é ilegível, e Dec(Enc(m,u),r) = m. Alternativamente, expressando isso por analogia, podemos pensar na “chave pública” de um usuário como sendo, na verdade, um design de fechadura específico, que outros usam para proteger as mensagens enviadas a eles, e na “chave privada” do usuário como a chave que abre a fechadura.

5. Um terceiro ainda pode ler as mensagens se obtiver acesso à chave privada do destinatário pretendido e interceptar a mensagem, se enganar o remetente para que associe o destinatário pretendido à sua própria chave privada, se conseguir instalar malware no remetente ou no dispositivo do destinatário e assim por diante. Além disso, existe o risco de que o desenvolvedor do aplicativo tenha deturpado a segurança ou o método de criptografia usado em seu aplicativo, como às vezes ocorre.

6. Por exemplo, digamos que meu par de chaves consiste na chave privada X e na chave pública Y. Se eu quiser dizer “Olá” e demonstrar que sou eu quem está dizendo isso, primeiro inserirei “Olá” e X no algoritmo de assinatura para produzir uma assinatura. Em seguida, enviarei uma mensagem com a palavra “Olá” seguida da assinatura. Finalmente, se você conhece minha chave pública, pode aplicar o algoritmo de verificação a “Olá”, Y e à assinatura e, assim, ver que fui eu quem assinou a mensagem.

7. Aqui, o Twitter está involuntariamente preenchendo o papel de Autoridade de Carimbamento Temporal (ACT). Ele está sendo confiável, em particular, tanto para produzir carimbos temporais autênticos (publicando tuítes com data precisa) quanto para garantir que esses carimbos temporais permaneçam disponíveis no futuro indefinido. Protocolos de carimbamento temporal mais sofisticados também podem remover essa segunda responsabilidade. Por exemplo, em vez de armazenar os hashes recebidos dos usuários, a ACT pode enviar de volta mensagens assinadas que contenham o hash e o momento de seu recebimento. Se o usuário mais tarde quiser convencer outras pessoas de que os dados existiam naquele momento, tudo o que eles precisam fazer é compartilhar a mensagem assinada junto com os dados. Mais segurança pode ser fornecida por propostas ainda mais sofisticadas, que substituem um ACT por várias partes confiáveis.

8. A terminologia aqui não é totalmente padronizada. No entanto, como nota técnica, os registros invioláveis podem ser classificados como uma variedade particular do que é conhecido como estruturas de dados autenticadas.

9. Como um benefício adicional de incluir ponteiros de hashes, Beto só precisa realmente saber o cabeçalho mais recente para detectar adulteração. Qualquer tentativa de Alice de passar uma sequência alternativa de cabeçalhos como legítima seria frustrada pela óbvia inconsistência da sequência com aquela que Beto conhece.

34. Hoje, o esquema de criptografia homomórfica mais amplamente aplicável é provavelmente o esquema de criptografia de Paillier, que é homomórfico sob adição, ao mesmo tempo que permite a multiplicação entre inputs criptografadas e não criptografadas. Isso é suficiente para calcular qualquer função linear de dados criptografados.

---

Publicado originalmente em maio de 2021 e disponível aqui.

Autor: Ben Garfinkel

Centre for the Governance of AI – Future of Humanity Institute
Universidade de Oxford

Tradução: Luan Marques