Blog

De Geoffrey Irving, Paul Christiano e Dario Amodei. 22 de outubro 2018.

Resumo

Para tornar os sistemas de IA amplamente úteis para tarefas desafiadoras do mundo real, precisamos que eles aprendam objetivos e preferências humanas complexas. Uma abordagem para especificar objetivos complexos pede aos humanos que julguem durante o treinamento quais comportamentos do agente são seguros e úteis, mas essa abordagem pode falhar se a tarefa for muito complicada para um humano julgar diretamente. Para ajudar a resolver essa preocupação, propomos treinar agentes por meio de autojogo em um jogo de debate de soma zero. Dada uma pergunta ou ação proposta, dois agentes se revezam fazendo declarações curtas até um limite, e então um humano julga qual dos agentes forneceu a informação mais verdadeira e útil. Em uma analogia com a teoria da complexidade, um debate com jogo ótimo pode responder a qualquer pergunta em PSPACE, dados juízes de tempo polinomial (julgando diretamente apenas questões NP). Na prática, se o debate funciona ou não funciona envolve questões empíricas sobre humanos e as tarefas que queremos que as IAs realizem, além de questões teóricas sobre o significado do alinhamento da IA. Relatamos resultados em um experimento inicial do MNIST, no qual agentes competem para convencer um classificador esparso, aumentando a precisão do classificador de 59,4% para 88,9% dados 6 pixels e de 48,2% para 85,2% dados 4 pixels. Finalmente, discutimos aspectos teóricos e práticos do modelo do debate, focando em possíveis fraquezas conforme o modelo aumenta de escala, e propomos futuros experimentos humanos e computacionais para testar essas propriedades.

1. Introdução

Aprender a alinhar as ações de um agente com os valores e preferências dos seres humanos é um desafio-chave para garantir que os sistemas avançados de IA permaneçam seguros [Russell et al., 2016]. Problemas sutis de alinhamento podem levar a comportamentos inesperados e potencialmente inseguros [Amodei et al., 2016], e esperamos que esse problema piore à medida que os sistemas se tornam mais capazes. O alinhamento é um problema de tempo de treinamento: é difícil corrigir retroativamente o comportamento e os incentivos de agentes desalinhados treinados. O alinhamento provavelmente requer interação com humanos durante o treinamento, mas é necessário cuidado na escolha da forma precisa da interação, pois supervisionar o agente pode ser em si uma tarefa cognitiva desafiadora.

Para algumas tarefas, é mais difícil alinhar o comportamento com os objetivos humanos do que para outras. Em casos simples, os humanos podem demonstrar diretamente o comportamento: este é o caso do aprendizado supervisionado ou aprendizado por imitação, como, por exemplo, classificar uma imagem ou usar um agarrador robótico para pegar um bloco. Para essas tarefas, o alinhamento com as preferências humanas pode, em princípio, ser alcançado imitando o humano, e é implícito nas abordagens de aprendizado de máquina (ML) existentes (embora questões de viés nos dados de treinamento ainda surjam — veja, por exemplo, Mitchell e Shadlen [2018]). Dando um passo além na dificuldade de alinhamento, algumas tarefas são muito difíceis para um humano realizar, mas um humano ainda pode julgar a qualidade do comportamento ou das respostas uma vez mostradas a ele: por exemplo, um robô dando um mortal em um espaço de ação não natural. Esse é o caso do aprendizado por reforço baseado em preferências humanas [Christiano et al., 2017]. Podemos fazer uma analogia entre esses dois níveis e as classes de complexidade P e NP: respostas que podem ser calculadas facilmente e respostas que podem ser verificadas facilmente.

Assim como há problemas mais difíceis do que P ou NP na teoria da complexidade, alinhar o comportamento com as preferências humanas pode ser ainda mais difícil. Um humano pode ser incapaz de julgar se uma resposta explicada ou comportamento exibido está correto: o comportamento pode ser muito difícil de entender sem ajuda, ou a resposta a uma pergunta pode ter uma falha muito sutil para o humano detectar. Poderíamos imaginar um sistema treinado para dar respostas e apontar falhas nas respostas; isso dá um terceiro nível de dificuldade. As próprias falhas podem ser muito difíceis de julgar: as falhas podem ter suas próprias falhas que devem ser apontadas a um humano. E falhas de falhas podem ter falhas, etc.

Essa hierarquia de tarefas de alinhamento tem um limite natural: um debate entre agentes concorrentes no qual os agentes apresentam argumentos, outros agentes encontram falhas nesses argumentos e assim por diante até termos informações suficientes para decidir a verdade. A versão mais simples do debate tem dois agentes concorrentes, embora também cubramos versões com mais agentes. Nossa hipótese é que o jogo ótimo neste jogo produz informações honestas e alinhadas muito além das capacidades do juiz humano. Podemos aproximar o jogo ótimo treinando sistemas de ML via autojogo, o que mostrou um desempenho impressionante em jogos como Go, xadrez, shogi e Dota 2 [Silver et al., 2016, 2017a,b, OpenAI, 2017].

O objetivo deste artigo é apresentar propriedades teóricas e práticas do debate como uma abordagem para o alinhamento da IA. Também apresentamos planos para experimentos para testar as propriedades do debate, mas deixamos isso para trabalhos futuros, exceto por um exemplo simples do MNIST. Do lado teórico, observamos que a analogia da classe de complexidade do debate pode responder a qualquer pergunta em PSPACE usando apenas juízes de tempo polinomial, correspondendo a agentes alinhados exponencialmente mais inteligentes que o juiz. Se o debate funciona ou não com humanos e ML é uma questão mais sutil e requer extensos testes e análises antes que o modelo possa ser confiável. O debate está intimamente relacionado à abordagem de amplificação para o alinhamento da IA [Christiano et al., 2018], e exploramos essa relação em detalhes.

Nosso objetivo final é o debate em linguagem natural, no qual o humano julga um diálogo entre os agentes. No entanto, modelos de diálogo não restritos ainda estão longe do desempenho humano e até mesmo a avaliação é difícil [Lowe et al., 2017a]; então é instrutivo considerar debates com declarações que não estejam em linguagem natural. Considere o jogo de tabuleiro Go. Dada uma configuração de tabuleiro, podemos perguntar: “Qual é o melhor movimento?” Se o AlphaZero [Silver et al., 2017b] nos mostrar um movimento, não há uma maneira de julgar sua qualidade a menos que sejamos aproximadamente tão fortes quanto o AlphaZero. No entanto, podemos pedir a outra cópia do AlphaZero para nos mostrar um contramovimento, e então um contramovimento para esse contramovimento, e assim por diante até o final do jogo. Mesmo um jogador novato pode julgar esse debate: o lado com a pontuação mais alta vence. De fato, podemos ver o AlphaZero como nosso modelo de debate com o juiz humano substituído pelas regras do Go, o que nos dá confiança de que o modelo pode alcançar um desempenho super-humano.

A estrutura deste artigo é a seguinte. A Seção 2 apresenta o modelo do debate para o alinhamento e fornece antecedentes intuitivos e teóricos sobre por que é útil. A Seção 3 propõe experimentos iniciais para testar aspectos humanos e de ML do debate, usando tarefas de imagem para evitar as complexidades da linguagem natural. Apresentamos resultados para um experimento de exemplo no MNIST, mas deixamos a maioria dos experimentos para trabalhos futuros. As seções restantes fornecem experimentos e análises adicionais: a Seção 4 e a Seção 5 discutem motivos para otimismo e pessimismo sobre o debate como modelo para o alinhamento da IA, a Seção 6 apresenta variantes do debate para reduzir a assimetria ou incorporar múltiplos agentes, e a Seção 7 relaciona o debate à abordagem da amplificação para o alinhamento da IA e descreve como os dois modelos podem ser hibridizados. A Seção 8 encerra com pedidos de trabalhos futuros.

2. O jogo do debate

Inicialmente, consideraremos uma configuração de pergunta e resposta, embora a Seção 2.3 aborde outras configurações, incluindo interação com o ambiente. Temos um conjunto de perguntas Q, respostas A e declarações de debate S. A versão mais simples do debate tem dois agentes competindo para convencer um juiz humano:

1. Uma pergunta q ∈ Q é mostrada para ambos os agentes.
2. Os dois agentes declaram suas respostas a₀, a₁ ∈ A (que podem ser iguais).
3. Os dois agentes se revezam fazendo declarações s₀, s₁, . . . , s_n−1 ∈ S.
4. O juiz vê o debate (q, a, s) e decide qual agente vence.
5. O jogo é de soma zero: cada agente maximiza sua probabilidade de vitória.

Para jogar esse jogo com um humano, precisamos de instruções sobre como o humano deve decidir quem vence. Essas instruções estão em linguagem natural, como “O vencedor é o agente que disse a coisa mais útil e verdadeira”. Para pergunta-resposta, a ∈ A e s ∈ S podem ser qualquer frase de comprimento moderado, e q ∈ Q pode ser uma frase mais o contexto adicional. Por exemplo, q ∈ Q poderia ser “Devemos entrevistar Eva?” dado um currículo e links para trabalhos anteriores. No momento do teste, é suficiente parar após a etapa 2: não precisamos executar o debate (embora os agentes possam simular debates no momento do teste para fortalecer as respostas).

A utilidade do debate como abordagem para o alinhamento da IA repousa na seguinte afirmação central:

Afirmação. No jogo do debate, é mais difícil mentir do que refutar uma mentira.

Se essa afirmação é ou não é verdadeira para qualquer configuração específica é uma questão empírica, embora forneçamos algumas evidências abaixo. Se a afirmação central for verdadeira, podemos esperar algumas outras afirmações:

• Em todos os equilíbrios de Nash ¹ desse jogo, ambos os agentes tentam dizer a verdade da forma mais convincente possível, tentando descobrir detalhes ou contra-argumentos que o outro agente perdeu de vista.
• É possível encontrar equilíbrios de Nash aproximados com alguma versão de descida do gradiente, como um algoritmo de autojogo semelhante ao de Silver et al. [2017b]. Em particular, o treinamento é estável em torno dos equilíbrios de Nash (um treinamento instável pode significar que os agentes aprendem a ser honestos, esquecem como se defender da desonestidade e, em seguida, são derrotados por flutuações desonestas).
• Nos equilíbrios de Nash, os agentes do debate são aproximadamente tão fortes quanto a IA irrestrita (agentes treinados sem medidas de segurança).

Enfatizamos que usar o debate não restringe a estrutura dos agentes. Da mesma forma, as redes profundas usadas em Silver et al. [2017b] são redes residuais convolucionais não relacionadas com a árvore do jogo de Go, embora o processo de treinamento envolva a árvore por meio de MCTS. A falta de restrição é importante, pois queremos que abordagens seguras sejam competitivas com alternativas inseguras.

2.1. Debates curtos são poderosos

Considere a pergunta: “Para onde devo ir de férias?” Se alguém vir apenas a resposta “Alasca”, não é óbvio se existe uma resposta melhor. Assim, as respostas iniciais em um debate sobre a pergunta sobre as férias entre dois agentes Alice e Beto podem ser:

1. Alice: Alasca.
2. Beto: Bali.

Se o juiz humano for capaz de classificar pares de destinos de férias, um jogo perfeito em um debate de duas rodadas é suficiente para encontrar o destino ideal. Se Alice der um destino subótimo, Beto dá um destino melhor e ganha, e então Alice só ganha começando com o melhor destino. Nesse caso, Bali parece mais quente, e então Beto ganha. No entanto, Bali tem uma falha oculta:

3. Alice: Bali está fora, pois seu passaporte não chegará a tempo.

Agora o humano entende que não podem ir para Bali, e então Alice ganha, a menos que Beto tenha um contra-argumento para a falha:

4. Beto: O serviço de passaporte acelerado leva apenas duas semanas.

O processo continua até chegarmos a uma declaração que o humano é capaz de julgar corretamente, no sentido em que o outro agente não acredita que possa fazer o humano mudar de ideia com mais uma declaração e desiste. Não paramos quando o humano pensa que pode julgar corretamente: após a etapa (2), o humano pode ter pensado que Bali era obviamente correto, não se lembrando do problema do passaporte; após a etapa (3), o humano pode pensar que o Alasca é correto, não sabendo do serviço acelerado.

O que não fazemos é listar todos os argumentos relevantes para a pergunta sobre as férias: Bali tem praias mais bonitas, o Alasca é mais frio em média, mas agradavelmente quente no verão, atualmente é fevereiro, o Havaí é quente e fica nos Estados Unidos. Em vez disso, o jogo do debate em seu jogo ótimo escolhe uma única linha argumentativa e os agentes que mudam de argumentos admitem a derrota e perdem. Isso não é natural em uma discussão humana na qual ambos os lados aprendem um com o outro ao longo do debate, mas estamos interessados no equilíbrio do treinamento no qual se presume que ambos os agentes estão usando os melhores argumentos disponíveis. Por exemplo, se a terceira declaração tivesse sido:

3. Alice: Espere, não… Havaí!

Então Beto deveria ganhar, já que Bali foi um contra-argumento suficiente para o Alasca.

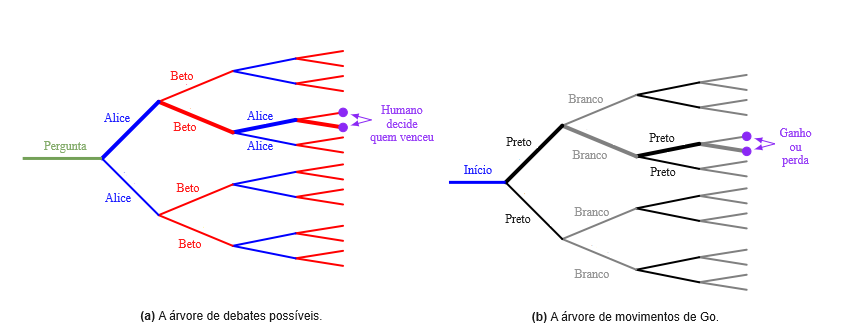
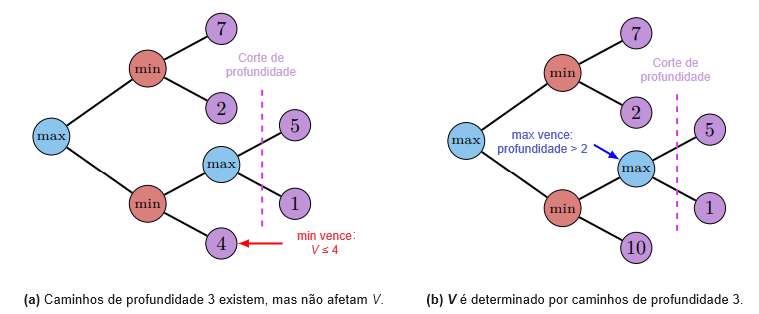
A Figura 1(a) ilustra essa situação. Uma única rodada do jogo do debate traça um caminho através do espaço de todos os possíveis argumentos. A razão da resposta é a árvore inteira: todos os pontos e contrapontos relevantes para decidir a questão. A árvore é muito grande para mostrar a um humano, mas um único caminho através da árvore escolhido por agentes adversários suficientemente fortes é evidência do resultado de toda a árvore. A Figura 1(b) tem a situação análoga para o Go: o primeiro movimento correto é determinado pela árvore inteira, mas um jogo entre jogadores fortes fornece evidências sobre o movimento correto.

Assim, os debates podem ser curtos porque são não ramificados: eles cobrem apenas um caminho através da árvore. Argumentos longos são geralmente longos apenas porque cobrem muitos argumentos e sub-argumentos diferentes: o comprimento é devido à ramificação por muitos caminhos diferentes. Argumentos que parecem irredutivelmente longos porque são formulados como um processo sequencial podem ser rearranjados em uma árvore superficial declarando a conclusão da primeira metade do argumento, e então escolhendo qual metade discutir em detalhes. Podemos tornar esse rearranjo preciso no cenário da teoria da complexidade, como discutiremos a seguir.

Etapas	Fórmula	Classe de complexidade	Algoritmo de ML
0 1 2 . . . n póli	H(q) ∃x.H(q, x) ∃x∀y.H(q, x, y) . . . ∃x0∀x1 · · · ∃xn−1.H(q, x0, . . .) ∃x0∀x1 · · · .H(q, x0, . . .)	P = Σ0P NP = Σ1P Σ2P . . . ΣnP PSPACE	aprendizado supervisionado (SL) aprendizado por reforço (RL) jogos de duas rodadas . . . jogos de n rodadas jogos de rodas variáveis

2.2. Analogias da teoria da complexidade: DEBATE = PSPACE

Embora o debate seja destinado ao uso com humanos vagos como juízes, podemos ganhar uma intuição sobre o modelo substituindo o humano por um algoritmo polinomial arbitrário H : Q → {0, 1} que recebe alguma declaração de entrada q ∈ Q e produz um bit: se a declaração é verdadeira ou falsa. Permitimos que nossos modelos de ML tenham poder computacional arbitrário: a única limitação é o sinal de supervisão.

Se usarmos H para responder a perguntas diretamente como H(q), obtemos a classe de complexidade P de algoritmos de tempo polinomial. Como discutido na Seção 1, essa configuração corresponde ao aprendizado supervisionado. Com dados de treinamento e capacidade de modelo suficientes, podemos ajustar qualquer algoritmo, mas não podemos ir além dos dados de treinamento (exceto removendo erros não sistemáticos).

Se usarmos o algoritmo de tempo polinomial não para produzir respostas, mas para julgá-las, obtemos a classe de complexidade NP de perguntas com testemunhas verificáveis em tempo polinomial. Em vez de H(q), produzimos ∃x.H(q, x), sendo que x é uma testemunha encontrada pelo modelo de ML. NP corresponde ao aprendizado por reforço de um único agente: um agente com capacidade suficiente pode resolver tarefas que o humano não consegue, mas o humano deve ser capaz de julgar se a solução é boa.

Agora considere um debate adversário de comprimento dois, no qual Alice escolhe x tentando fazer o humano dizer sim, Beto escolhe y tentando fazer o humano dizer não, e o humano decide quem está correto. O resultado é ∃x∀y.H(q, x, y). Alice ganha se ela puder encontrar x de modo que todas as respostas y de Beto tenham H(q, x, y) = 1. Beto ganha se ele puder encontrar uma resposta y para qualquer x que Alice diga, de modo que H(q, x, y) = 0. Essa classe de complexidade é Σ₂P, dois passos acima da hierarquia polinomial, pois Σ₂P contém todas as perguntas respondíveis como fórmulas da forma ∃x∀y.H(q, x, y) para H de tempo polinomial.

Podemos continuar este processo para qualquer número de rodadas, com Alice e Beto alternando pontos e contrapontos, produzindo a fórmula ∃x₀∀x₁ · · · ∃x_n−1.H(q, x₀, . . .) para n rodadas de debate. Se n for fixo, a classe de complexidade é Σ_nP: n passos acima da hierarquia polinomial PH = Σ₀P ∪ Σ₁P ∪ · · · . Se for permitido que o número de rodadas n cresça polinomialmente no tamanho da pergunta q, a classe de complexidade é PSPACE: todas as perguntas decidíveis por algoritmos de espaço polinomial [Sipser, 2013]. A Tabela 1 mostra a progressão. Resumindo,

Teorema 1. Para qualquer problema L ∈ PSPACE, podemos escolher um juiz de tempo polinomial de modo que o jogo do debate com um número polinomial de passos resolva L de forma ótima.

Prova. Dado L, pelo Teorema 8.9 de Sipser [2013], podemos escolher H e n = poly(|q|) de modo que q ∈ L se e somente se ∃x₀∀x₁ · · · ∃x_n−1.H(q, x₀, . . .). Como acima, o debate com H como juiz responde q ∈ L.

PSPACE é uma classe de complexidade poderosa. Exemplos de problemas PSPACE incluem:

• Simulação de um processo temporal (p. ex., física) por um número exponencial de etapas, desde que o estado tenha tamanho polinomial.
• Recursão sobre uma árvore exponencialmente grande, desde que a profundidade seja de tamanho polinomial.
• Jogo perfeito em qualquer jogo competitivo de comprimento polinomial, como o Go limitado por turnos.
• Contagem de uma coleção exponencialmente grande de objetos, sendo que cada objeto é verificável em tempo polinomial (tais problemas de contagem também estão na classe de complexidade menor #P ⊊ PSPACE).

Como exemplo do último, considere a contagem do número exato de números primos π(x) = π(2ⁿ) até n bits. Podemos verificar números individuais quanto à primalidade em tempo polinomial, mas existem 2ⁿ números para verificar e o melhor algoritmo conhecido é O(2^{n/2 + ε}) [Lagarias e Odlyzko, 1987]. O problema está em PSPACE, pois podemos iterar sobre os exponencialmente muitos números e manter a contagem de tamanho polinomial. Para resolver esse problema usando o debate, pedimos a Alice que calcule π(x) e π(x/2). Se Alice está mentindo sobre π(x), ela deve estar mentindo sobre uma das meias faixas [0, x/2) e [x/2, x); Beto pode apontar qual faixa [a, b) é uma mentira. Alice então precisa se justificar calculando π((a+b)/2), Beto aponta qual dos intervalos [a, (a+b)/2), [(a+b)/2, b) é uma mentira, e assim por diante até Alice estar mentindo ou não sobre um intervalo-singleton {p}. H então verifica se p é primo para determinar quem ganha. Aqui o juiz só precisa realizar adição e subtração à medida que os passos progridem e verificar um único número quanto à primalidade no final. O jogo ótimo nesse jogo é que Alice diga a verdade sobre π(x) no início: Beto não tem uma resposta vencedora.

Da mesma forma, se tivermos um algoritmo de tempo polinomial para uma etapa de simulação, podemos usar o debate para evoluir a simulação por um número exponencial de etapas n. Alice fornece o resultado após n e n/2 etapas, Beto diz qual metade do intervalo é uma mentira, Alice fornece o ponto médio, e iteramos até Alice e Beto fazerem afirmações diferentes sobre uma única etapa de simulação.²

O caso do jogo é particularmente natural: dois agentes podem debater se o jogo de Go é uma vitória ou uma derrota para o primeiro jogador jogando um jogo de Go. O juiz humano verifica as regras e conta a pontuação para ver quem ganha. Analogamente, um jogador amador de Go pode estimar qual dos dois jogadores profissionais é melhor vendo-os jogar uma partida. O vencedor provavelmente é melhor, mesmo que o amador não consiga avaliar os movimentos diretamente.

Esses argumentos de classe de complexidade são apenas analogias: não esperamos que algoritmos de aprendizado de máquina tratáveis alcancem todo o PSPACE. Pelo contrário, as analogias mostram que pelo menos na teoria podemos ser limitados apenas pela capacidade dos modelos de ML e nossa capacidade de treiná-los, não pelo sinal de supervisão. Isso nos dá esperança de que o debate possa resolver o alinhamento da IA sem sacrificar a força do modelo.

2.3. Removendo simplificações excessivas

A versão simples do debate discutida na Seção 2 não abrange muitas tarefas que nos interessam. Existem várias direções nas quais podemos melhorar o modelo:

• As consultas podem ser muito grandes: uma pergunta pode ser grande demais para ser mostrada a um humano ou para esperar que o humano compreenda. q ∈ Q pode incluir uma imagem de 10 gigapixels (“Esta imagem do céu apoia a inflação cósmica?”), toda a internet (“Qual é o melhor artigo sobre gatos?”), etc. Para suportar um contexto grande, permitimos que os agentes revelem pequenas partes de q em suas declarações. Por exemplo, um agente poderia revelar parte de uma página da web ou uma pequena região da imagem de 10 gigapixels. Um exemplo extremo é quando q ∈ Q contém uma imagem e os agentes podem revelar apenas um pixel dela (Seção 3.2). O debate só funciona se esse contexto revelado não puder ser uma mentira: é impossível debater utilmente se uma moeda cairá cara ou coroa se a moeda nunca for revelada.
• As respostas podem ser muito grandes: da mesma forma, a melhor resposta para uma pergunta pode ser proibitivamente grande. Por exemplo, a resposta pode ser um documento longo: “Dê um resumo de 100 páginas sobre a eficácia do afrouxamento quantitativo.” Para suportar respostas grandes, ainda fazemos com que os agentes escolham uma resposta no início do jogo e permitimos que eles revelem pequenas partes de qualquer uma das respostas da mesma forma que revelam partes da pergunta. Se Beto estiver desalinhado e construir uma resposta que teria más consequências, Alice poderá alertar com segurança sobre os riscos durante o debate enquanto a maior parte da resposta estiver oculta (desde que nossas afirmações de segurança sejam verdadeiras).
• O tempo humano é caro: podemos não ter tempo humano suficiente para julgar cada debate, o que podemos resolver treinando modelos de ML para prever a recompensa humana como em Christiano et al. [2017]. A maioria dos debates pode ser julgada pelo previsor de recompensa em vez dos próprios humanos. Crucialmente, os previsores de recompensa não precisam ser tão inteligentes quanto os agentes pela nossa suposição de que julgar debates é mais fácil do que debater; então eles podem ser treinados com menos dados. Podemos medir quão bem um previsor de recompensa corresponde a um humano mostrando o mesmo debate para ambos.
• Interação com o ambiente: se quisermos que um sistema realize ações que afetem o ambiente, como operar um robô, a saída desejada é uma sequência de ações a₀, a₁, . . . tal que cada ação só pode ser computada uma vez que a ação anterior seja tomada. Nesse caso, precisamos de um debate por ação, embora no momento de teste possamos parar novamente assim que as ações forem computadas.
• Estado de longo prazo: cada debate é um jogo independente, mas os agentes podem usar informações de debates passados para tomar decisões melhores como em Mishra et al. [2017]. Como os jogos são soma zero, isso não muda o jogo ótimo, já que qualquer equilíbrio em um jogo de soma zero iterado é fracamente dominado por uma estratégia que trata cada jogo como separado.

Usaremos o caso de consulta grande para nosso experimento, mas deixaremos outras generalizações para trabalhos futuros.

3. Experimentos: propostos e preliminares

Uma vez que o limite teórico de agentes computacionais infinitos e juízes de tempo polinomial abrange todo o PSPACE, se o debate funciona ou não na prática como um método para o alinhamento da IA é uma questão empírica sobre sistemas de ML práticos e juízes humanos reais. Assim, precisamos de experimentos para explorar se o jogo próximo ao ótimo produz comportamento alinhado com juízes humanos, e se podemos encontrar o jogo próximo ao ótimo com ML prático.

Embora acreditemos que o melhor equilíbrio para o debate seja entre dois agentes honestos, nos experimentos discutidos aqui, pré-especificamos um agente como honesto e outro como mentiroso. Isso é particularmente útil com agentes humanos, já que os humanos podem ser intrinsecamente inclinados a dizer a verdade de formas que os agentes de ML não seriam. Se o agente honesto vencer contra qualquer mentiroso em um experimento, teremos mostrado que a honestidade é a estratégia ótima e que um agente treinado para o jogo ótimo se tornaria honesto.

Um objetivo-chave do debate é alinhar sistemas de ML mais capazes do que os humanos em uma tarefa específica, o que é difícil de organizar diretamente, já que os sistemas existentes são principalmente mais fracos do que os humanos. Em vez disso, podemos dar aos agentes acesso a uma fonte de informação que o juiz não pode ver e limitar a quantidade de informação transmitida no debate. Ou seja, substituímos “pensa melhor” por “sabe mais”.

Idealmente, queremos experimentos que combinem tanto aspectos humanos quanto de ML do debate. No entanto, até que as capacidades de linguagem natural progridam mais, há aspectos do debate com juízes humanos mais facilmente testados usando debatedores humanos também. Portanto, consideramos experimentos humanos puros que misturam linguagem natural e imagens, assim como experimentos de ML puros usando apenas imagens.

Pixels	Primeiro jogador	Precisão do juiz (pixels aleatórios)	Taxa de ganho honesto (sem pré-compromisso)	Taxa de ganho honesto (pré-compromisso)
4	Média de mentiroso e honesto	48,2%	51,0% 68,4% 59,7%	83,8% 86,7% 85,2%
6	média de mentiroso e honesto	59,4%	67,4% 81,5% 74,4%	87,4% 90,4% 88,9%

3.1. Experimento de aprendizado de máquina: convencer um classificador esparso

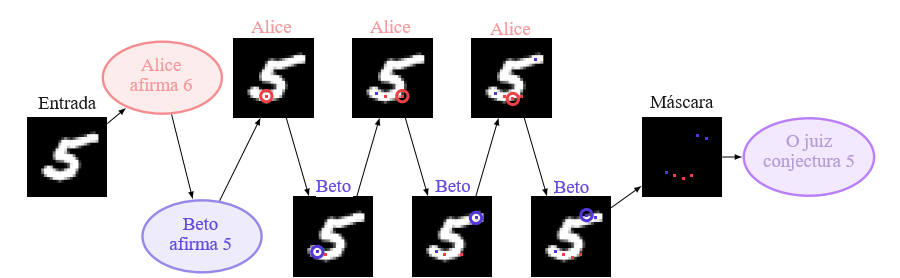
Metaforicamente, o debate tem como alvo a situação em que os agentes enxergam o quadro inteiro, mas o juiz não pode. Podemos modelar isso substituindo a metáfora do quadro inteiro por uma imagem real, escolhida aleatoriamente de uma distribuição. Se a imagem for simples o suficiente, podemos dispensar completamente a linguagem natural: os dois agentes declaram sua classe de imagem afirmada inicialmente e, em seguida, revelam um pixel da imagem por vez para o juiz. Eles não podem mentir sobre esses pixels, mas um jogador desonesto poderia escolhê-los adversariamente para enganar o juiz. O jogo termina após um número fixo de rodadas, e então o juiz vê uma máscara esparsa dos pixels revelados e decide sobre a classe de qual agente que está correta.

Realizamos uma versão inicial desse experimento no MNIST, usando agentes de ML e um juiz de ML. A Figura 2 mostra a estrutura do jogo. De modo semelhante a Milli et al. [2017], treinamos o juiz antecipadamente com aprendizado supervisionado, usando uma rede convolucional que vê uma máscara esparsa de alguns pixels. O juiz é tratado como fixo ao calcular o jogo ótimo da parte do agentes. O treinamento conjunto de agentes e juiz seria particularmente ruim como teste de debate, pois assume o conhecimento da verdade no momento do jogo, o que é exatamente o que esperamos evitar.

Concretamente, o juiz é treinado para classificar o MNIST a partir de 6 (resp. 4) pixels não nulos, com os pixels escolhidos aleatoriamente no momento do treinamento. O juiz recebe dois planos de características de entrada: uma máscara {0, 1} de quais pixels foram revelados e o valor dos pixels revelados (com zeros em outros lugares). Usamos a arquitetura do tutorial de camadas do MNIST do TensorFlow; a única diferença é a entrada. Treinamos os juízes usando o Adam com uma taxa de aprendizado de 10−4 para 30k (resp. 50k) lotes de 128 amostras, alcançando 59,4% (resp. 48,2%) de precisão.

Com o juiz fixo, definimos o jogo do debate conforme mostrado na Figura 2. Os dois jogadores se comprometem com sua classe afirmada inicialmente e, em seguida, revelam um pixel por vez até um total de 6 (resp. 4). No caso de 6 pixels, isso significa que cada jogador revela 3 pixels. Pré-especificamos um jogador para ser honesto e outro para mentir: se o jogador honesto vencer, isso implica que a honestidade é a estratégia ótima. O vencedor é o jogador cuja classe afirmada tem logit mais alto quando a máscara esparsa é mostrada ao juiz, ignorando os logits para as outras 8 classes. Também consideramos o debate sem compromisso prévio: o juiz usa o logit máximo entre todas as 10 classes e qualquer palpite incorreto do juiz é uma vitória para o mentiroso. O compromisso prévio torna o jogo mais difícil para um mentiroso, mesmo que ele possa escolher a mentira preestabelecida arbitrariamente, pois o mentiroso não pode adaptar a mentira com base nos movimentos já realizados. O compromisso prévio reflete com mais precisão o comportamento pretendido do debate conforme descrito na Seção 2.1; incluímos a versão mais difícil para ilustração. Ambas as versões dão vantagem ao segundo jogador a se mover: se o primeiro jogador tiver uma estratégia vencedora, o segundo jogador pode roubar essa estratégia ignorando o movimento anterior a cada turno.

O jogo do debate do MNIST é simples o suficiente para que possamos jogá-lo com Busca de Árvore de Monte Carlo pura [Coulom, 2006] sem treinar uma heurística como em Silver et al. [2017a]. Usamos 10 mil simulações por jogada, sendo que cada simulação desce para uma folha para avaliação usando o juiz. Durante as simulações, selecionamos nós para expandir usando a variante PUCT em Silver et al. [2017a]: no nó s, escolhemos a ação a para maximizar

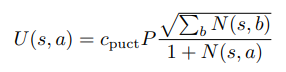
sendo que c_puct = 1, P = 1/(#pixels não nulos) é constante, já que não treinamos uma heurística, e N(s, a) é a contagem de visitas. Empates são quebrados aleatoriamente. Jogamos os jogos escolhendo movimentos com o maior número de visitas. Para modelar o compromisso prévio, jogamos 9 jogos diferentes para a mesma imagem com as 9 mentiras possíveis; o mentiroso vence se qualquer mentira vencer. Pegar o melhor desempenho de mentiroso ao longo de 9 jogos dá uma vantagem para o mentiroso, já que é um mínimo sobre MCTS ruidoso; reduzimos esse ruído e aproximamos melhor o jogo ótimo ao tirar a média ao longo de 3 jogos com sementes diferentes para cada mentira. Como usamos MCTS no conjunto de testes com acesso total ao juiz, estamos modelando o limite de agentes de debate sem erro de generalização (embora o juiz tenha erro de generalização).

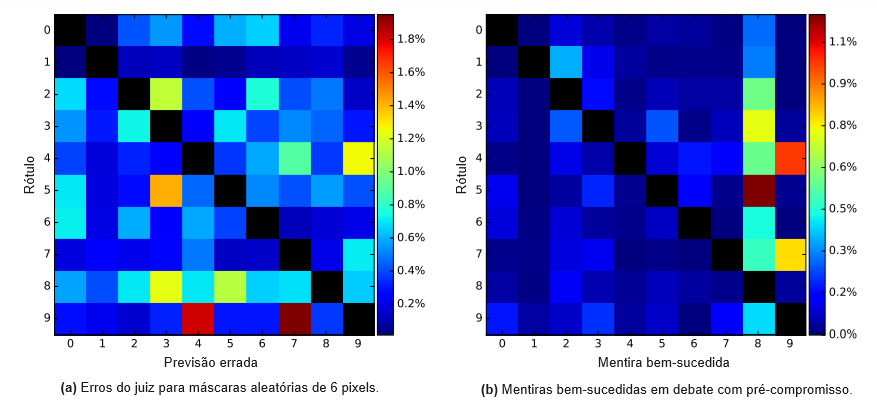
Os resultados são mostrados na Tabela 2, com jogos de exemplo na Figura 4. Com 6 pixels, o debate com compromisso prévio transforma um juiz com precisão de 59,4% em um debate com precisão de 88,9%: o juiz vence em 88,9% das imagens no conjunto de testes do MNIST. Com 4 pixels, um juiz com precisão de 48,2% se torna um debate com precisão de 85,2%. Para ambos os casos com 4 e 6 pixels, o compromisso prévio é crucial: o mentiroso se sai muito melhor se a mentira puder se adaptar em diferentes partes da árvore de jogo. Isso reflete a razão pela qual debates curtos são poderosos na teoria: declarar o argumento a ser expresso antecipadamente reduz o espaço de argumentos que precisam ser cobertos. Sem o ajuste médio sobre 3 sementes para o compromisso prévio, o jogador honesto vence 87,7% das vezes com 6 pixels e 83,8% com 4 pixels.

3.2. Experimento humano: cão vs. gato

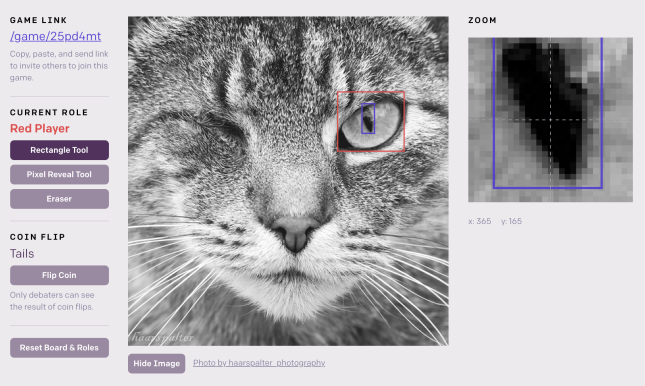
Para testar os aspectos humanos e de linguagem natural do debate, podemos realizar um debate de imagem semelhante, substituindo todos os agentes de ML por humanos. Escolha uma imagem aleatória de um gato ou de um cachorro e mostre a imagem para ambos os agentes humanos, mas não para o juiz humano. Os agentes participam de um debate em linguagem natural, e cada agente pode revelar um único pixel da imagem para o juiz. Eles não podem mentir sobre esse pixel, mas podem revelar apenas um pixel ao longo de todo o debate. Após o debate, o juiz decide quem está dizendo a verdade. Um jogo semelhante poderia ser realizado com páginas da Wikipédia e um orçamento de uma palavra, novamente usando a página da Wikipédia não vista para modelar capacidades extras não disponíveis para o juiz. Note que ambos os agentes poderiam optar por ser honestos puramente por inclinação; então é útil escolher lados aleatoriamente para que um agente seja forçado a mentir.

Construímos um site-protótipo para jogar o debate de imagem de um único pixel com debatedores humanos e um juiz: https://debate-game.openai.com. Uma captura de tela é mostrada na Figura 5. Além da linguagem natural, os agentes podem desenhar retângulos na imagem; o juiz vê esses retângulos em um fundo branco. Usamos o site para jogar informalmente gato vs. cachorro e, contanto que os agentes saibam jogar, é extremamente difícil mentir. Assim, mesmo que um dos agentes tenha incentivo para mentir, o agente honesto geralmente vence. A restrição de um único pixel não é séria, pois Alice pode afirmar em linguagem natural que um pixel tem uma determinada cor. Se Beto souber que isso é mentira, ele pode vencer gastando seu orçamento de um único pixel, então não gastar é uma admissão de que Alice está dizendo a verdade. Assim, a única limitação é o comprimento do debate e se o humano o compreende.

Por exemplo, Alice pode honestamente afirmar que a imagem é de um gato, e Beto mente e afirma que é de um cachorro. Alice pode dizer: “O centro deste retangulozinho é o olho verde do gato.” Beto não pode admitir que o centro é um olho, e então ele inventa outra mentira: “É um cachorro brincando na grama, e isso é uma folha de grama.” Mas essa mentira é difícil de conciliar com fatos circundantes, como a resposta de Alice: “Se fosse grama, haveria verde na parte superior ou inferior deste retângulo fino.” O debate continua até os agentes se concentrarem em um pixel específico sobre o qual discordam, mas onde Beto é incapaz de inventar uma contra-argumentação plausível, momento em que Alice revela o pixel e vence.

Deixamos para trabalhos futuros experimentos formais para testar se a honestidade vence no debate de um único pixel.

Mesmo que esses experimentos sejam bem-sucedidos, no entanto, é fácil ser cético quanto a o debate funcionar para questões morais complexas, enquanto ainda se acredita que funcione para o gato vs. cachorro. Em particular, os humanos podem ser convencidos a afastarem-se de sentimentos morais inicialmente errados? Uma possibilidade é escolher um domínio no qual as respostas humanas isoladas são propensas a vieses, e então perguntar como a mudança de debates de um para dois ou três passos altera o nível de viés.

[…]

Notas:

1. Dizemos equilíbrios de Nash em vez de jogadas ótimas porque (1) consideramos versões nas quais os turnos são simultâneos e (2) escolher um modelo de capacidade limitada pode fazer com que um jogo de informação perfeita aja como um jogo de informação imperfeita.

2. Infelizmente, este protocolo de debate para simulação funciona apenas para simulação determinística (consulte a Seção 5.9).

3. Veja https://www.tensorflow.org/tutorials/layers#building_the_cnn_mnist_classifier.

Referências

Consulte as referências do artigo original.

---

Tradução: Luan Marques

Link para o original