Blog

De Tom Everitt, Ryan Carey, Lewis Hammond, James Fox, Eric Langlois e Shane Legg

Cerca de 2 anos atrás, divulgamos os primeiros artigos sobre entender os incentivos dos agentes usando diagramas de influência causal. Este post irá resumir o progresso feito desde então.

O que são diagramas de influência causal?

Um problema-chave no alinhamento da IA é entender os incentivos dos agentes. Foram levantadas preocupações de que os agentes podem ser incentivados a evitar a correção, manipular os usuários ou influenciar inapropriadamente o seu aprendizado. Isso é particularmente preocupante, já que esquemas de treinamento muitas vezes moldam incentivos de maneiras sutis e surpreendentes. Por esses motivos, estamos desenvolvendo uma teoria formal de incentivos baseada em diagramas de influência causal (DICs).

Aqui está um exemplo de um DIC para um processo decisório de Markov (MDP) de uma etapa. A variável aleatória S₁ representa o estado no tempo 1, A₁ representa a ação do agente, S₂, o estado no tempo 2, e R₂, a recompensa do agente.

[imagem]

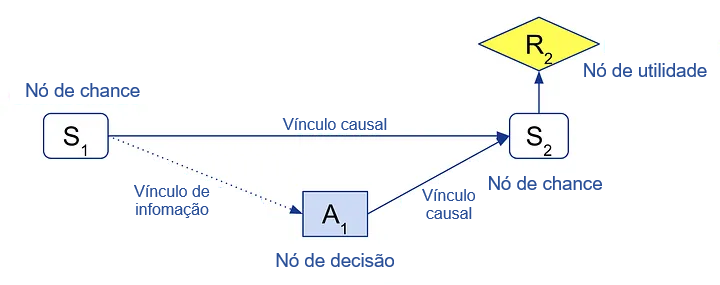
A ação A₁ é modelada com um nó de decisão (quadrado) e a recompensa R₂ é modelada como um nó de utilidade (diamante), enquanto os estados são nós de chance normais (arestas arredondadas). Os vínculos causais especificam que S₁ e A₁ influenciam S₂ e que S₂ determina R₂. O vínculo de informação S₁ → A₁ especifica que o agente conhece o estado inicial S₁ ao escolher sua ação A₁.

Em geral, variáveis aleatórias podem ser escolhidas para representar pontos de decisão do agente, objetivos e outros aspectos relevantes do ambiente.

Em suma, um DIC especifica:

• Decisões do agente
• Objetivos do agente
• Relacionamentos causais no ambiente
• Restrições de informação do agente

Essas informações são frequentemente essenciais ao tentar entender os incentivos de um agente: como um objetivo pode ser alcançado depende de como ele está relacionado causalmente a outros aspectos (influenciáveis) no ambiente, e a otimização de um agente é limitada pelo acesso às informações que possui. Em muitos casos, os julgamentos qualitativos expressos por um DIC (não parametrizado) são suficientes para inferir aspectos importantes dos incentivos, com suposições mínimas sobre detalhes de implementação. Por outro lado, foi demonstrado que é necessário conhecer os relacionamentos causais no ambiente para inferir incentivos; então muitas vezes é impossível inferir incentivos com menos informações do que as expressas por um DIC. Isso torna os DICs representações naturais para muitos tipos de análise de incentivos.

Outras vantagens dos DICs são que eles se baseiam em tópicos bem pesquisados como causalidade e diagramas de influência, permitindo-nos aproveitar o pensamento profundo que já foi feito nesses campos.

Conceitos de incentivo

Ter uma linguagem unificada para configurações de treinamento e objetivos nos permite desenvolver conceitos e resultados geralmente aplicáveis. Definimos quatro desses conceitos em Incentivos de Agentes: uma Perspectiva Causal (AAAI-21):

• Valor de informação: o que o agente deseja saber antes de tomar uma decisão?
• Incentivo de resposta: a que mudanças no ambiente os agentes ótimos respondem?
• Valor de controle: o que o agente deseja controlar?
• Incentivo de controle instrumental: o que o agente está interessado em controlar e é capaz de controlar?

Por exemplo, no MDP de uma etapa acima:

• Para S₁, um agente ótimo agiria de forma diferente (ou seja, responderia) se S₁ mudasse, e valorizaria saber e controlar S₁, mas não pode influenciar S₁ com sua ação. Então, S₁ tem valor de informação, incentivo de resposta e valor de controle, mas não tem um incentivo de controle instrumental.
• Para S₂ e R₂, um agente ótimo não poderia responder a mudanças, nem conhecê-las antes de escolher sua ação; então eles não têm valor de informação nem incentivo de resposta. Mas o agente valorizaria controlá-los e é capaz de influenciá-los; então S₂ e R₂ têm valor de controle e incentivo de controle instrumental.

[imagem]

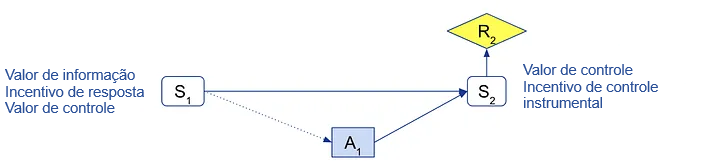
No artigo, provamos critérios gráficos sólidos e completos para cada um deles, de modo que possam ser reconhecidos diretamente a partir de uma representação gráfica do DIC (consulte postagens anteriores).

Valor de informação e valor de controle são conceitos clássicos que existem há muito tempo (contribuímos para os critérios gráficos), enquanto incentivos de resposta e incentivos de controle instrumental são novos conceitos que descobrimos ser úteis em várias aplicações.

Para os leitores familiarizados com iterações anteriores deste artigo, observamos que alguns dos termos foram atualizados. Os incentivos de controle instrumental anteriormente eram chamados apenas de “incentivos de controle”. O novo nome enfatiza que é controle como um objetivo instrumental, em oposição ao controle que surge como um efeito colateral (ou devido à informação mútua). Valor de informação e valor de controle anteriormente eram chamados de “incentivos de observação” e “incentivos de intervenção”, respectivamente.

Intervenções e interrupção do usuário

Vamos agora analisar algumas aplicações recentes desses conceitos. No artigo “Como os Agentes de RL se Comportam quando suas Ações são Modificadas” (AAAI-21), estudamos como diferentes algoritmos de aprendizado por reforço (RL) reagem a intervenções do usuário, como interrupções e ações sobrescritas. Por exemplo, Saunders et al. desenvolveram um método para exploração segura, no qual um usuário sobrescreve ações perigosas. Alternativamente, os agentes podem ser interrompidos se a análise de seus “pensamentos” (ou ativações internas) sugerir que estão planejando algo perigoso. Como tais intervenções afetam os incentivos de vários algoritmos de RL?

Primeiro, formalizamos a modificação de ações estendendo MDPs com um parâmetro PA que descreve a modificação de ações. Em seguida, modelamos esses MDPs de ação modificada com um DIC:

[imagem]

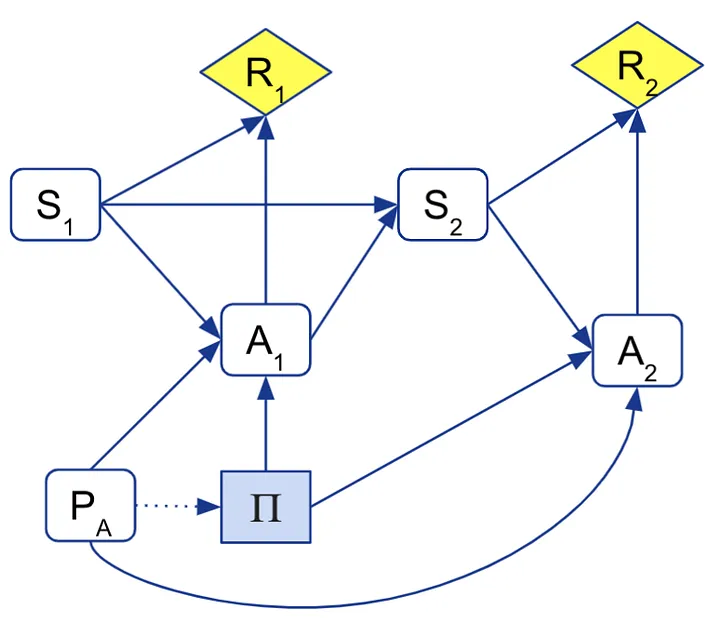
Aqui modelamos a diretriz Π do agente como a decisão em vez das ações A_i, já que elas não estão completamente sob o controle do agente, mas também podem ser influenciadas pela modificação de ações PA (como representado pelas setas PA → A_i e Π → A_i). O agente pode conhecer o esquema de interrupção PA a partir de interrupções durante o treinamento; então incluímos um vínculo de informação PA → Π.

Analisamos diferentes algoritmos prototípicos de RL em termos das suposições causais que fazem sobre o ambiente:

• Algoritmos de otimização de caixa-preta, como estratégias evolutivas, levam em consideração todos os relacionamentos causais.
• Em contraste, a regra de atualização do Q-learning pressupõe efetivamente que a próxima ação será realizada de forma ótima, sem modificação de ações. Isso significa que os Q-learners ignoram os efeitos causais PA → A_i. Da mesma forma, o SARSA com a ação escolhida pelo agente na atualização de TD pressupõe que estará no controle de sua próxima ação. Chamamos essa versão de SARSA virtual.
• O SARSA baseado na ação modificada (SARSA empírico) ignora o efeito da modificação de ações na ação atual, mas leva em consideração o efeito nas ações subsequentes.

Podemos representar as diferenças com os seguintes DICs. (O nó de diretriz Π’ para o SARSA empírico representa que as ações são otimizadas separadamente, não conjuntamente.)

[imagem]

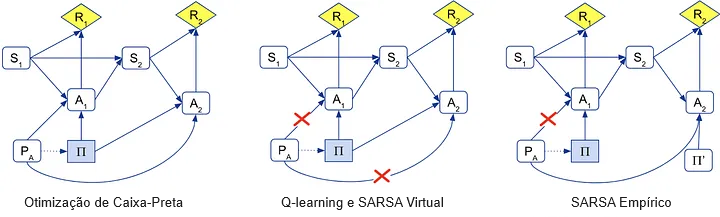
Os DICs podem ser usados para entender como os diferentes algoritmos se adaptam à interrupção, por meio de um critério gráfico para incentivos de resposta específicos ao caminho. A otimização de caixa-preta tenta obscurecer sua diretriz e desativar seu interruptor de desativação, enquanto o Q-learning e o SARSA Virtual não fazem nenhum dos dois. O SARSA empírico tenta desativar o interruptor de desativação, mas não tenta obscurecer sua diretriz.

Verificamos empiricamente esses resultados nos gridworlds relevantes de segurança da IA, bem como em um novo ambiente onde o agente precisa se comportar bem na simulação para ser implementado na realidade, onde otimizadores de caixa-preta exibem um comportamento semelhante à “virada traiçoeira“. Os resultados são uma generalização dos resultados de interrupção de Orseau e Armstrong para o Q-learning e o SARSA.

Olhando de forma mais ampla, esses resultados são um bom exemplo de análise causal de algoritmos de aprendizado de máquina. Diferentes escolhas de projeto se traduzem em diferentes suposições causais, que por sua vez determinam os incentivos. Em particular, a análise destaca por que os diferentes incentivos surgem, aprofundando assim nossa compreensão de como o comportamento é moldado.

Manipulação da recompensa

Outro problema de segurança da IA que estudamos com DICs é a manipulação da recompensa. A manipulação da recompensa pode assumir várias formas diferentes, incluindo o agente:

• alterar o código-fonte de sua função de recompensa implementada (“wireheading”),
• influenciar os usuários que treinam um modelo de recompensa aprendido (“manipulação do feedback”),
• manipular as entradas que a função de recompensa usa para inferir o estado (“manipulação da entrada da FR / problemas de caixa de delírios”).

Por exemplo, o problema de um agente influenciar sua função de recompensa pode ser modelado com o seguinte DIC, no qual RF_i representa a função de recompensa do agente em diferentes etapas temporais e os vínculos vermelhos representam um incentivo indesejável de controle instrumental.

[imagem]

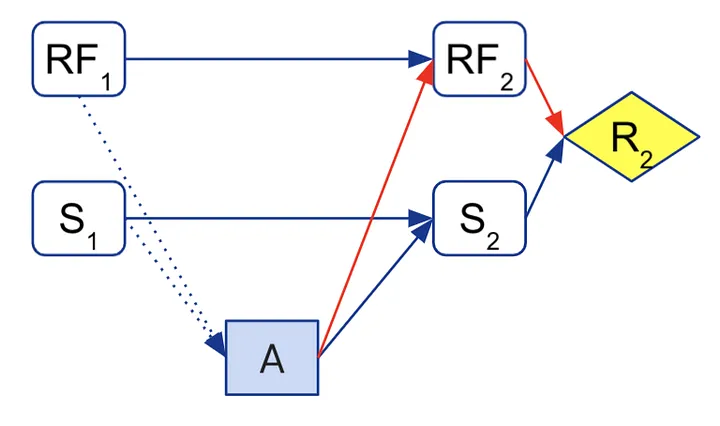
No artigo “Problemas e Soluções de Manipulação da Recompensa” (publicado na respeitada revista de filosofia Synthese), modelamos todos esses diferentes problemas com DICs, bem como uma variedade de soluções propostas, como otimização da FR atual, aprendizado de recompensas não influenciáveis e funções de utilidade baseadas em modelos. Curiosamente, embora essas soluções tenham sido inicialmente desenvolvidas independentemente de análises causais formais, todas evitam incentivos indesejáveis cortando alguns vínculos causais de forma a evitar incentivos de controle instrumental.

Ao representar essas soluções em uma estrutura causal, podemos ter uma melhor compreensão de por que elas funcionam, quais suposições elas requerem e como se relacionam entre si. Por exemplo, a otimização da FR atual e as funções de utilidade baseadas em modelos formulam um objetivo modificado em termos de uma variável aleatória observada de uma etapa temporal anterior, enquanto o aprendizado de recompensas não influenciáveis (como o CIRL) usa uma variável latente:

[imagem]

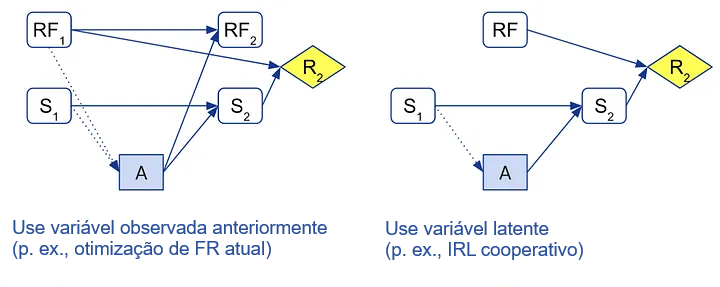
Como consequência, aqueles primeiros métodos precisam lidar com a inconsistência temporal e a falta de incentivo para aprender, enquanto estes últimos requerem a inferência de uma variável latente. Provavelmente dependerá do contexto se um é preferível ao outro, ou se uma combinação é melhor do que qualquer um deles sozinho. Independentemente disso, ter destilado as ideias-chave deve nos colocar em uma posição melhor para aplicar flexivelmente as percepções em cenários novos.

Consulte a postagem anterior para um resumo mais longo da otimização da FR atual. O próprio artigo foi significativamente atualizado desde as pré-impressões compartilhadas anteriormente.

DICs multiagentes

Muitos problemas interessantes de incentivo surgem quando múltiplos agentes interagem, cada um tentando otimizar sua própria recompensa enquanto simultaneamente influenciam a recompensa um do outro. No artigo “Refinamentos de Equilíbrio em Diagramas de Influência Multiagentes” (AAMAS-21), nos baseamos no trabalho seminal de Koller e Milch para estabelecer fundamentos para entender situações multiagentes com DICs multiagentes (DICMAs).

Primeiro, relacionamos DICMAs a jogos em forma extensiva (EFGs), atualmente as representações gráficas mais populares de jogos. Embora os EFGs às vezes ofereçam representações mais naturais de jogos, eles têm algumas desvantagens significativas em comparação com os DICMAs. Em particular, os EFGs podem ser exponencialmente maiores, não representam independências condicionais e carecem de variáveis aleatórias para aplicar análise de incentivos.

Como exemplo, considere um jogo no qual uma loja (Agente 1) decide (D¹) se vai cobrar o preço integral (F) ou a metade (H) por um produto, dependendo de seus níveis de estoque atuais (X), e um cliente (Agente 2) decide (D²) se vai comprar (B) ou passar (P), dependendo do preço e de quanto ele quer o produto (Y). A loja tenta maximizar seu lucro U¹, que é maior se o cliente comprar a um preço alto. Se ela tiver excesso de estoque e o cliente não comprar, então ela tem que pagar aluguel extra. O cliente está sempre feliz em comprar pela metade do preço, e às vezes pelo preço inteiro (dependendo de quanto ele quer o produto).

A representação em EFG desse jogo é bastante grande e usa conjuntos de informações (representados com arcos pontilhados) para representar os fatos de que a loja não sabe quanto o cliente deseja o produto e que o cliente não sabe os níveis de estoque atuais da loja:

[imagem]

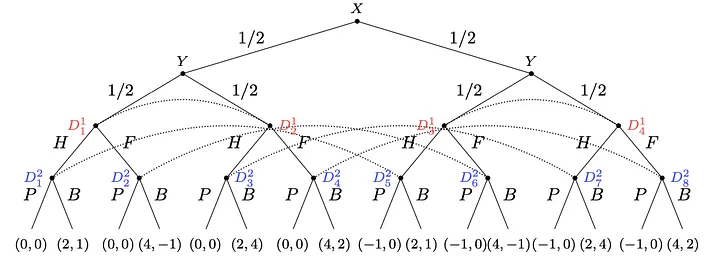
Por outro lado, a representação do DICMA é significativamente menor e mais clara. Em vez de depender de conjuntos de informações, o DICMA usa vínculos de informação (arestas pontilhadas) para representar a informação limitada disponível para cada jogador:

[imagem]

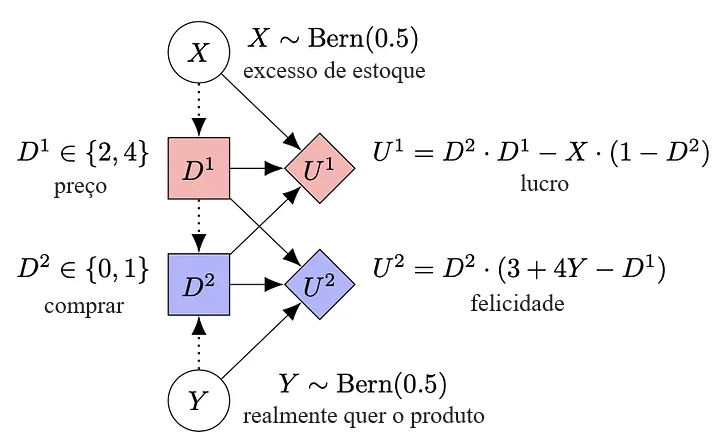
Outro aspecto que fica mais claro no DICMA é que, para qualquer decisão fixa do cliente, a recompensa da loja é independente de quanto o cliente queria o produto (não há uma aresta Y→U¹). Da mesma forma, para qualquer preço fixo do produto, a recompensa do cliente é independente dos níveis de estoque da loja (não há uma aresta X→U²). No EFG, essas independências só poderiam ser inferidas olhando cuidadosamente para as recompensas.

Um benefício de os DICMAs representarem explicitamente essas independências condicionais é que mais partes do jogo podem ser identificadas como solucionáveis de forma independente. Por exemplo, no DICMA, o seguinte componente solucionável de forma independente pode ser identificado. Chamamos esses componentes de subjogos do DICMA:

[imagem]

Resolver esse subjogo para qualquer valor de D¹ revela que o cliente sempre compra quando realmente quer o produto, independentemente de haver um desconto. Esse conhecimento torna mais simples calcular a estratégia ótima para a loja em seguida. Por outro lado, no EFG, os conjuntos de informações impedem a identificação de quaisquer subjogos adequados. Portanto, resolver jogos usando uma representação de DICMA geralmente é mais rápido do que usar uma representação de EFG.

Por fim, relacionamos vários tipos de conceitos de equilíbrio entre DICMAs e EFGs. O tipo mais famoso de equilíbrio é o equilíbrio de Nash, que ocorre quando nenhum jogador pode melhorar unilateralmente sua recompensa. Um refinamento importante do equilíbrio de Nash é o equilíbrio perfeito em subjogos, que exclui ameaças não críveis, exigindo que um equilíbrio de Nash seja jogado em todos os subjogos. Um exemplo de ameaça não credível no jogo loja-cliente seria o cliente “ameaçando” a loja a comprar apenas com desconto. A ameaça é não crível, pois a melhor jogada para o cliente é comprar o produto mesmo pelo preço integral, se ele realmente o quer. Curiosamente, apenas a versão de DICMA de perfeição em subjogos é capaz de eliminar tais ameaças, porque apenas no DICMA a escolha do cliente é reconhecida como um subjogo adequado.

Por fim, nosso objetivo é usar DICMAs para analisar incentivos em ambientes multiagentes. Com as observações acima, nos colocamos em posição de desenvolver uma teoria dos incentivos multiagentes que esteja adequadamente conectada à literatura mais ampla da teoria dos jogos.

Software

Para nos ajudar em nossa pesquisa sobre DICs e incentivos, desenvolvemos uma biblioteca em Python chamada PyCID, que oferece:

• uma sintaxe conveniente para definir DICs e DICMAs;
• métodos para calcular diretrizes ótimas, equilíbrios de Nash, d-separation, intervenções, consultas de probabilidade, conceitos de incentivo, critérios gráficos e muito mais,
• geração aleatória de CID(MA)s e exemplos pré-definidos.

Nenhuma configuração é necessária, pois os blocos de notas de tutoriais podem ser executados e estendidos diretamente no navegador, graças ao Colab.

Também disponibilizamos um pacote Latex para desenhar DICs e lançamos o site causalincentives.com como um local para coletar links para os vários artigos e softwares que estamos produzindo.

Olhando para o futuro

Por fim, esperamos contribuir para uma compreensão mais cuidadosa de como o design, o treinamento e a interação moldam o comportamento de um agente. Esperamos que uma linguagem precisa e amplamente aplicável baseada em DICs possibilite raciocínios e comunicações mais claros sobre essas questões e facilite uma compreensão cumulativa de como pensar e projetar sistemas de IA poderosos.

Dessa perspectiva, achamos encorajador que vários outros grupos de pesquisa tenham adotado DICs para:

• analisar os incentivos de agentes não ambiciosos para sair de sua caixa,
• explicar o aprendizado de recompensas não influenciáveis e esclarecer suas propriedades desejáveis (veja também a Seção 3.3 no artigo da manipulação da recompensa),
• desenvolver uma nova estrutura para tornar os agentes indiferentes às intervenções humanas.

Atualmente, estamos seguindo várias direções de pesquisa a mais:

• Estendendo os conceitos gerais de incentivo para múltiplas decisões e múltiplos agentes.
• Aplicando-os à justiça e a outras configurações de segurança da IA.
• Analisando limitações que foram identificadas até agora. Em primeiro lugar, considerando as questões levantadas por Armstrong e Gorman. E em segundo lugar, examinando conceitos mais amplos do que incentivos de controle instrumental, já que a influência também pode ser incentivada como um efeito colateral de um objetivo.
• Investigando mais a fundo suas bases filosóficas e estabelecendo uma semântica mais clara para os nós de decisão e utilidade.

Esperamos ter mais novidades em breve!

Gostaríamos de agradecer a Neel Nanda, Zac Kenton, Sebastian Farquhar, Carolyn Ashurst e Ramana Kumar pelos comentários úteis sobre esboços deste post.

Lista de artigos recentes:

• Agent Incentives: A Causal Perspective
• How RL Agents Behave When Their Actions Are Modified
• Reward tampering problems and solutions in reinforcement learning: A causal influence diagram perspective
• Equilibrium Refinements for Multi-Agent Influence Diagrams: Theory and Practice

Veja também causalincentives.com

---

Tradução: Luan Marques

Link para o original