Blog

De Eliezer Yudkowsky

Resumo

Quase todas as teorias da decisão concordam em usar a noção de “utilidade esperada” como base das definições de agente e escolha racional. As teorias da decisão diferem exatamente em como calcular a expectativa: a probabilidade de um resultado, condicionada a uma ação.

Essa diferença fundamental se reflete em questões da vida real sobre votar em eleições, ou aceitar uma oferta baixa na mesa de negociação. Quando você está pensando no que acontece se não votar em uma eleição, deve calcular o resultado esperado como se apenas o seu voto mudasse, ou como se todas as pessoas suficientemente semelhantes a você também decidissem não votar?

Perguntas como essas pertencem a uma classe maior de problemas, problemas de decisão de tipo Newcomb, nos quais algum outro agente é similar a nós ou raciocina sobre o que faremos no futuro. O princípio central das “teorias lógicas da decisão”, várias famílias das quais serão introduzidas, é que devemos escolher como se estivéssemos controlando a saída lógica de nosso algoritmo de decisão abstrato.

Considerações de tipo Newcomb — que inicialmente podem parecer casos especiais incomuns — se tornam mais proeminentes à medida que agentes podem obter informações de alta qualidade sobre quais algoritmos ou diretrizes outros agentes usam: compromissos públicos, agentes artificiais com códigos conhecidos, contratos inteligentes rodando no Ethereum. Considerações de tipo Newcomb também se tornam mais importantes à medida que lidamos com agentes muito semelhantes uns aos outros, ou com grandes grupos de agentes que provavelmente contêm subgrupos de alta semelhança, ou com problemas em que mesmo pequenas correlações são suficientes para mudar a decisão.

Na filosofia, o debate sobre teorias de decisão é visto como um debate sobre o princípio da escolha racional. Agentes “racionais” se abstêm de votar em eleições, porque é muito improvável que o seu voto mude algo? Precisamos ir além da “racionalidade”, para a “racionalidade social” ou “super-racionalidade” ou algo assim, a fim de descrever agentes que teriam a possibilidade de compor uma sociedade funcional? Agentes racionais às vezes desejam ser irracionais? Algumas teorias da decisão foram acusadas de entrar em ciclos infinitos em problemas de tipo Newcomb; a escolha racional pode ser indefinida? (Teóricos lógicos da decisão respondem “Não”.) Se você estivesse construindo uma teoria da decisão em uma inteligência artificial, qual teoria da decisão você usaria e quais seriam as consequências de construir um agente assim?

Esta visão geral aborda primeiro o Dilema do Prisioneiro, um dos problemas clássicos de tipo Newcomb que é fundamental para a teoria dos jogos e para problemas de coordenação na economia. Fala sobre o jogo do Dilema do Prisioneiro entre dois agentes que conhecem o código-fonte um do outro; para motivar a próxima seção, que apresenta a motivação para a teoria da decisão atualmente mais aceita, e introduz a nova noção de “teoria lógica da decisão” ou agentes que escolhem como se estivessem controlando as saídas lógicas de seus algoritmos. Esta visão geral então aborda alguns dos argumentos mais filosóficos que foram apresentados sobre o que devemos considerar como sendo o princípio da escolha racional e resume rapidamente algumas das consequências pragmáticas. […]

O status acadêmico geral da teoria lógica da decisão é “um novo desafiante para a teoria da decisão atualmente dominante, mas a maioria das pessoas nunca ouviu falar dela, embora isso esteja começando a mudar”.

O Dilema do Prisioneiro

Na apresentação clássica do Dilema do Prisioneiro, você e seu colega assaltante de banco foram presos e encarcerados. Vocês não podem se comunicar um com o outro. Estão enfrentando uma sentença de prisão de um ano cada. Ambos receberam a oportunidade de trair o outro (Desertar); alguém que Deserta diminui um ano da sua própria sentença de prisão, mas acrescenta dois anos à sentença de prisão da outra pessoa. Alternativamente, você pode Cooperar com o outro prisioneiro ficando em silêncio.

Portanto, se (o1, o2) é o resultado para o Jogador 1 e o Jogador 2, respectivamente, a matriz de resultados para o clássico Dilema do Prisioneiro é:

	Jogador 2 Deserta:	Jogador 2 Coopera:
Jogador 1 Deserta:	(2 anos, 2 anos)	(0 ano, 3 anos)
Jogador 1 Coopera:	(3 anos, 0 ano)	(1 ano, 1 ano)

Reescrevendo isso como um jogo com jogadas D e C, e ganhos positivos sendo que $X denota “X utilidade”:

	D2	C2
D1	($1, $1)	($3, $0)
C1	($0, $3)	($2, $2)

Na teoria da decisão paradigmática atual, é considerado “racional” (abordaremos o debate sobre esse termo em breve) para um jogador egoísta jogar Desertar no Dilema do Prisioneiro. Isso é preocupante porque, se dois jogadores “racionais” jogam Desertar, isso leva ao resultado ($1, $1), que é dominado de Pareto pelo resultado ($2, $2), que ambos os jogadores prefeririam. Parece que há uma maneira para ambas as partes se saírem melhor, o que, na teoria-padrão, dois agentes racionais não conseguem obter para si mesmos.

Houve muitas objeções ao cenário que leva a essa conclusão preocupante. Por exemplo: “No mundo real, você teria algum sentimento de camaradagem pelo seu conspirador e valorizaria negativamente sua sentença de prisão; pessoas reais não são completamente egoístas.” Ou, “Desertar no Dilema do Prisioneiro arruinaria sua reputação e talvez levasse a represálias depois que você saísse da prisão.” Podemos tentar construir um Verdadeiro Dilema do Prisioneiro modificando as circunstâncias para lidar com essas objeções: por exemplo, duas instituições de caridade que cada qual acredita firmemente que sua missão é mais importante, que ambas conhecem alguns fatos prejudiciais sobre a outra instituição de caridade e que estão em reuniões privadas e secretas com um filantropo decidindo como dividir o financiamento entre elas.

No Dilema do Prisioneiro Iterado (DPI), jogamos o Dilema do Prisioneiro contra o mesmo agente 100 vezes seguidas. No DPI, uma estratégia famosa, Tit for Tat, faz o que o outro jogador fez na rodada anterior e começa cooperando. Essa estratégia geralmente se sai extremamente bem em torneios de bots, mesmo quando joga contra programas muito mais complicados.

Suponha que dois agentes “racionais” (ou seja, racionais de acordo com a teoria da decisão paradigmática atual) joguem o Dilema do Prisioneiro Iterado com um horizonte de tempo conhecido: ambos os agentes sabem que o jogo termina após a 100ª rodada. Então, na 100ª rodada, ambos os agentes irão Desertar, já que essa jogada não tem consequências futuras. Na 99ª rodada, ambos os agentes, sabendo que o outro irá Desertar independentemente na 100ª rodada, também irá Desertar. Por indução, dois agentes com conhecimento comum definitivo de que ambos os agentes são “racionais” (em vez de o outro agente possivelmente ser Tit for Tat como alternativa) irão Desertar um contra o outro em todas as rodadas.

Mesmo aceitando a configuração básica e sua matriz de resultados, diversos filósofos e cientistas da computação tiveram dificuldade em aceitar que agentes racionais devem desertar no Dilema do Prisioneiro, muito menos que agentes com conhecimento comum da racionalidade de cada um devem passar 100 rodadas desertando no DPI. Douglas Hofstadter sugeriu que a “super-racionalidade” incluiria levar em conta que o outro agente estava raciocinando em uma situação muito semelhante à sua e que ambos provavelmente chegariam a respostas racionais semelhantes, seja qual fosse a resposta racional.

Dilema do Prisioneiro com Conhecimento Comum de Códigos

Imagine um torneio do Dilema do Prisioneiro no qual bots enviados competem entre si no Dilema do Prisioneiro de uma única rodada, mas com conhecimento do código do outro bot.¹ Este é o problema do “equilíbrio dos programas” proposto por Tennenholtz em 2010.

No mínimo (como observou Tennenholtz), neste torneio você pode se sair do que desertando o tempo todo: você pode perceber quando o código do outro bot é uma cópia exata do seu próprio código e, nesse caso, cooperar. Mas será possível fazer ainda melhor?

Suponha que você se encontre enfrentando um bot assim:

def FairBot1(outroAgente):
   se (outroAgente(FairBot1) == Cooperar):
     retorne Cooperar
   senão:
     retorne Desertar

Se você fosse um bot enfrentando o FairBot1 (ou se preferir, imagine que uma inteligência artificial razoavelmente inteligente esteja enfrentando o FairBot1), então pareceria claro que a decisão inteligente é Cooperar com o FairBot1.

O próprio FairBot1, apesar da semelhança com o Tit for Tat, definitivamente não é um jogador ótimo no torneio do Dilema do Prisioneiro que acabamos de definir. Uma razão é que o FairBot1 coopera com o CooperateBot.

def CooperateBot(outroAgente):
  retorne Cooperar

(Talvez ajude visualizar o CooperateBot como uma pedra com a palavra “cooperar” escrita em si mesma, para ajudar a bombear a intuição de que você deve desertar quando há apenas uma pedra do outro lado.)

Também se observa que quando o FairBot1 joga contra uma cópia de si mesmo, ambos os agentes entram em um ciclo infinito e nunca retornam um valor.

O seguinte algoritmo para corrigir o problema do ciclo infinito pode parecer irrealista à primeira vista, mas pode ser executado em um tempo muito mais curto do que se poderia esperar.

Primeiro, escolha um sistema de prova simples, como a aritmética de primeira ordem. Vamos chamar esse sistema de prova de T de “teoria”.

Denote “T prova a frase citada S” escrevendo Prov(T, ⌜S⌝).

Em seguida, reescreva o Fairbot2 para dizer:

def Fairbot2(outroAgente):
  se (Prov(T, "outroAgente(Fairbot2) == Cooperar")):
    retorne Cooperar
  senão:
    retorne Desertar

…ou seja, “Eu coopero, se eu provar que o outro agente coopera”.

Surpreendentemente, isso não leva a nenhum regresso infinito! Você pode pensar que parece igualmente consistente supor tanto “Dois Fairbot2s desertam, e portanto ambos não provam que o outro coopera” quanto “Ambos os FairBot2s cooperam, e portanto ambos provam que o outro coopera”, com o primeiro equilíbrio parecendo mais provável por causa do problema do ovo e da galinha. Na verdade, uma regra estranha chamada teorema de Löb implica que ambos os agentes provam a Cooperação e, portanto, ambos Cooperam.

Ainda mais surpreendentemente: quando temos sistemas complexos de “A é verdadeiro se B é comprovável e C não é comprovável” mais “C é verdadeiro se é comprovável que a consistência de T implica B e D” etc., podemos calcular exatamente o que é e o que não é comprovável em tempo polinomial.

O resultado é que, se tivermos sistemas complicados de agentes que fazem X se podem provar que outros agentes fariam Y se estivessem jogando contra Z, etc., podemos avaliar quase imediatamente o que realmente acontece.

Um dos primeiros artigos em teoria lógica da decisão, “Cooperação Resiliente no Dilema do Prisioneiro: Equilíbrio de Programa Através da Lógica de Comprobabilidade“, exibiu uma prova (com código em execução) de que existia um agente simples PrudentBot que:

• Cooperava com outro PrudentBot.
• Cooperava com o FairBot2.
• Desertava contra o CooperateBot (também conhecido como uma pedra com a palavra “Cooperar” escrita em si mesma).
• Não era explorável (o PrudentBot nunca joga Cooperar quando o outro jogador joga Desertar).

… e mais tarde foi mostrado que o PrudentBot era um caso especial de algo que se parece com uma regra de tomada de decisão mais geral e unificada, a teoria da decisão baseada na prova, que por sua vez é uma variante de uma teoria lógica da decisão.

Diferentes Cálculos de Utilidade Esperada

Você pode ter ouvido afirmarem que não é “racional” votar em eleições, já que o seu próprio voto tem apenas uma probabilidade muito pequena de mudar o resultado da eleição.

Quando as pessoas falam de “racionalidade” nesse sentido, elas estão apelando a uma formulação da teoria da decisão chamada “teoria causal da decisão” (também conhecida como TCD), a formulação mais próxima que existe de uma formulação-padrão atual da racionalidade. A TCD diz que o princípio da escolha racional é calcular a utilidade esperada de acordo com as consequências causais do seu ato físico (em um sentido formal que definiremos em breve). A menos que o seu voto faça muitas outras pessoas votarem, ao invés de todos vocês estarem em situações semelhantes, a TCD diz que o seu voto provavelmente não causará uma mudança no resultado da eleição.

A nova família de teorias da decisão a ser apresentada, as teorias lógicas da decisão, incorpora o que se argumenta ser um candidato melhor para o princípio da escolha racional: devemos escolher como se estivéssemos decidindo a saída lógica do nosso algoritmo de decisão.

As eleições são um dos casos em que a TLD faz uma grande diferença no que parece ser racional ou normativo, em comparação com a TCD clássica. As populações votando em eleições são grandes o suficiente para que possa haver muitas outras pessoas com algoritmos de decisão semelhantes ao seu — nem todo o mundo, mas um grupo logicamente correlacionado grande o suficiente para que isso possa ser importante. Você pode razoavelmente acreditar que todos na sua coorte provavelmente decidirão votar (ou não votar) de forma semelhante, e perguntar se o benefício provável de toda a coorte votar vale o custo de toda a coorte votar.

O debate sobre problemas de decisão de tipo Newcomb acabam girando em torno da questão de como definir formalmente “A probabilidade de um resultado, condicionada à escolha X” dentro dos cálculos de utilidade esperada.

Condicionamento Evidencial versus Contrafactual

Quase todos no campo da teoria da decisão concordam que alguma versão de utilidade esperada é central para a racionalidade; existem conjuntos inteiros de teoremas de coerência mostrando que várias formas de vingança bizarra são aplicadas aos agentes cujo comportamento não pode ser visto como consistente com algum conjunto de crenças probabilísticas e uma função de utilidade.

Se você já leu um livro-texto discutindo a noção de “utilidade esperada”, ele provavelmente a definiu como algo como:

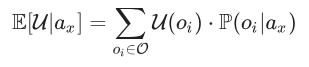
sendo que:

• E[U|a_x] é nossa expectativa média de utilidade, se a ação a_x é escolhida;
• O é o conjunto de resultados possíveis;
• U é a nossa função de utilidade, que mapeia resultados em números reais;
• P(o_i|a_x) é a probabilidade condicional do resultado o_i se a_x é escolhida.

É de concordância praticamente universal que essa fórmula está errada.

O problema é o uso do condicionamento evidencial em P(o_i|a_x). Nessa fórmula, estamos nos comportando como se estivéssemos perguntando: “Qual seria a minha probabilidade revisada para P(o_i|a_x) se me informassem a notícia ou se eu observasse a evidência de que minha ação tinha sido a_x?”

A teoria causal da decisão (o padrão atual) diz que devemos, em vez disso, usar o condicional contrafactual P(a_x □→ o_i ).

A diferença entre o condicionamento evidencial e o contrafactual é contrastada de forma-padrão por estas duas frases:

• Se Lee Harvey Oswald não atirou em John F. Kennedy, outra pessoa atirou.
• Se Lee Harvey Oswald não tivesse atirado em John F. Kennedy, outra pessoa o teria atirado.

Na primeira frase, estamos recebendo a informação como a notícia de que Oswald não atirou em Kennedy e atualizando nossas crenças de acordo para combinar com o mundo que já vimos. No segundo mundo, estamos imaginando como um mundo contrafactual teria se desenrolado se Oswald tivesse agido de forma diferente

Se K denota a proposição de que outra pessoa atirou em Kennedy e O denota a proposição de que Oswald atirou nele, então a primeira frase e a segunda frase estão respectivamente falando sobre:

• P(K|¬O)
• P(¬O □→ K )

Calcular utilidade esperada usando condicionamento evidencial é amplamente aceito como algo que leva a uma diretriz irracional de “gerenciar as notícias”. Por exemplo, suponha que a toxoplasmose, uma infecção parasitária transmitida por gatos, possa fazer com que os humanos infectados por ela se tornem mais apegados aos gatos.²

Agora você está diante de um gato fofo que foi examinado por um veterinário que diz que este gato definitivamente não tem toxoplasmose. Se você decidir acariciar o gato, um observador imparcial vendo você concluirá que você tem 10% mais chances de ter toxoplasmose, o que pode ser uma infecção bastante prejudicial. Se você não acariciar o gato, perderá o prazer hedônico de acariciá-lo. Você acaricia o gato?

A maioria dos teóricos da decisão concorda que, nesse caso, você deve acariciar o gato. Ou você já tem toxoplasmose ou não tem. Acariciar o gato não pode fazer você adquirir toxoplasmose. Você apenas estaria perdendo a sensação agradável de acariciar o gato.

Depois, você pode atualizar suas crenças com base na observação de sua própria decisão e perceber que tinha toxoplasmose o tempo todo. Mas, ao considerar as consequências das ações, você deve raciocinar que, se contrafactualmente não tivesse acariciado o gato, você ainda teria toxoplasmose e teria perdido a chance de acariciar o gato. (Assim como, se Oswald não tivesse atirado em Kennedy, ninguém mais teria.)

A teoria da decisão que afirma que devemos condicionar nossas ações por meio da fórmula-padrão da probabilidade condicional, como se estivéssemos sendo informados de nossas escolhas como uma notícia ou fazendo atualização bayesiana nas nossas ações como observações, é chamada de teoria evidencial da decisão. A teoria evidencial da decisão responde à pergunta central “Como devo condicionar minhas escolhas?” com a réplica: “Condicione suas escolhas como se as estivesse observando como evidência” ou “Realize a ação que consideraria melhor se a ouvisse como notícia”.

(Para uma crítica mais severa da teoria evidencial da decisão mostrando como agentes mais espertos podem bombear dinheiro de agentes decisórios evidenciais, veja o Dilema do Cupim.)

Contrafactuais Causais

A Teoria Causal da Decisão, o padrão acadêmico atual, diz que a fórmula da utilidade esperada deve ser escrita assim:

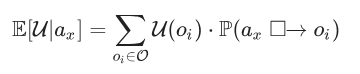
Isso nos leva à questão de como calculamos P(a_x □→ o_i ).

Na literatura filosófica, muitas vezes se presume que sabemos intuitivamente quais devem ser os resultados contrafactuais. (P. ex., estamos simplesmente presumindo que de alguma forma você sabe que, se Oswald não tivesse atirado em Kennedy, ninguém mais teria; isso é intuitivamente óbvio.) Isso é formalizado tendo uma distribuição condicional P( • || • ) que é tratada como enviada dos céus e inclui todos os condicionais contrafactuais.

Se não ficarmos satisfeitos em deixar as coisas assim (e não deveríamos ficar), podemos importar a teoria dos modelos causais desenvolvida por Judea Pearl et. al. A teoria dos modelos causais estabelece formalmente como realizar uma cirurgia contrafactual em modelos gráficos de processos causais.

Formalmente, temos um grafo acíclico dirigido como:

•  X₁-> {$X_2$, X₃} -> X₄ -> X₅

Um dos exemplos de tal grafo causal de Judea Pearl é:

• ESTAÇÃO -> {CHOVENDO, ASPERSOR} -> {CALÇADA} -> {ESCORREGADIA}

Isso diz, por exemplo:

• Que a estação atual afeta a probabilidade de estar CHOVENDO e, separadamente, afeta a probabilidade de o ASPERSOR ligar. (Mas CHOVENDO e ASPERSOR não afetam um ao outro; se sabemos a estação atual, não precisamos saber se está CHOVENDO para descobrir a probabilidade de o ASPERSOR estar ligado.)
• CHOVENDO e ASPERSOR podem ambos causar que a CALÇADA fique molhada. (Então, se observássemos que a calçada está molhada, então mesmo já sabendo a estação, estimaríamos uma probabilidade diferente de que estivesse CHOVENDO, dependendo de se o ASPERSOR estivesse ligado. O ASPERSOR ligado “explicaria” a umidade observada da CALÇADA sem nenhuma necessidade de postular CHOVENDO.)
• A CALÇADA estar molhada é o único fator determinante para a CALÇADA está ESCORREGADIA. (Então, se sabemos se a CALÇADA está molhada, não descobrimos nada mais sobre a probabilidade de que o caminho está ESCORREGADIO ao sermos informados de que a estação é verão. Mas se não soubéssemos se a CALÇADA estava molhada, se a estação fosse verão ou outono poderia ser muito relevante para conjecturar se o caminho estava ESCORREGADIO!)

Um modelo causal vai além do grafo ao incluir funções de probabilidade específicas P( X_i | pa_i) para calcular a probabilidade de cada nó X_i assumindo o valor x_i dado os valores pa_i dos antecessores imediatos de x_i. Presume-se implicitamente que o modelo causal se fatoriza, de modo que a probabilidade de qualquer atribuição de valores x ao grafo inteiro possa ser calculada usando o produto:

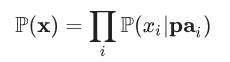
Então, o condicional contrafactual P(x | do( X_j = x_j ) é calculado via:

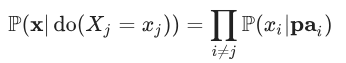
(Presumimos que x tenha x_j igualando o valor especificado por do de X_j; caso contrário, sua probabilidade condicionada é definida como 0.)

Isso é na verdade bastante simples; apenas diz que, quando definimos do( X_j = x_j ), ignoramos os nós genitores comuns para X_j e simplesmente dizemos que, independentemente dos valores de pa_i, a probabilidade de X_j = x_j é 1.

Essa fórmula implica — como intuitivamente se esperaria — que condicionar a do( X_j = x_j ) só pode afetar as probabilidades de variáveis X_k que estão “a jusante” de X_j no grafo acíclico dirigido que é a espinha dorsal do modelo causal. De maneira muito semelhante a (normalmente) pensarmos que nossas escolhas hoje afetam quanto dinheiro teremos amanhã, mas não quanto dinheiro tínhamos ontem.

Então, a utilidade esperada deve ser calculada como:

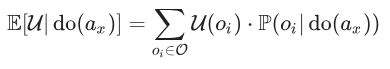
Sob essa regra, não calcularemos que podemos afetar a probabilidade de ter toxoplasmose ao acariciar o gato, já que nossa escolha de acariciar o gato está causalmente a jusante de se temos toxoplasmose.

Comichões e Ciclos Infinitos

Uma classe de problemas técnicos com a teoria causal da decisão surge da forma como, no caso do Dilema da Toxoplasmose, chegamos à decisão qualitativa correta, porém à resposta quantitativa errada para a utilidade esperada.

Suponha que a probabilidade anterior de ter toxoplasmose seja de 10% e que a probabilidade posterior após ser visto acariciando o gato seja de 20%. Suponha que não ter toxoplasmose tenha utilidade de $ 100, que ter toxoplasmose tenha utilidade de $ 0 e que, dado o quanto você gosta de acariciar gatos, acariciar o gato adicione $ 1 de utilidade ao seu resultado.

Então, a fórmula acima para decidir se deve acariciar o gato sugere que acariciar leva a uma utilidade esperada de $ 91 e não acariciar leva a uma utilidade esperada de $ 90. Isso nos diz para acariciar o gato, o que é a decisão correta, mas também nos diz para esperar $ 91 de utilidade esperada após acariciar o gato, sendo que na verdade recebemos $ 81 em expectativa. Parece que a resposta intuitivamente “correta” é que deveríamos calcular $ 81 de utilidade para acariciar o gato e $ 80 de utilidade para não acariciá-lo.

Você pode inicialmente ser tentado a resolver esse problema fazendo o cálculo em fases:

• Fase 1: calcule a decisão com base nas crenças anteriores.
• Fase 2: atualize nossas crenças com base na observação de nossa preferência emergente: percebemos o “comichão” de um impulso para decidir de uma maneira específica.
• Fase 3: recalcule as utilidades esperadas com base nas crenças posteriores, possivelmente escolhendo uma nova ação; então volte para 2.

…e então aguarde que esse algoritmo se estabeleça em um estado consistente.

Além de carecer da eficiência e elegância de calcular nossa decisão de uma vez, parece possível para um agente como esse entrar em um ciclo infinito. Houve propostas para quebrar esse ciclo infinito randomizando ações. Mas então acabamos novamente calculando as probabilidades de resultados errados condicionados à ação que realmente realizamos, e isso pode levar a outras decisões aparentemente estúpidas.

O Problema de Newcomb e o Caronista de Parfit

O debate acadêmico sobre a teoria da decisão girava principalmente em torno de problemas de decisão de tipo Newcomb, uma classe ampla que inclui o Dilema do Prisioneiro, votação em eleições, coordenação com outros agentes que estão raciocinando sobre você, e assim por diante.

Grosso modo, poderíamos descrever problemas de tipo Newcomb como aqueles em que alguém semelhante a você, ou tentando prever você, existe no ambiente. Nesse caso, sua decisão pode se correlacionar com eventos fora de você, sem que sua ação cause fisicamente esses eventos.

O problema de Newcomb original era bastante artificial, mas vale a pena recontar por razões históricas:

Um alienígena chamado Ômega apresenta a você duas caixas, uma caixa transparente A contendo $ 1.000 e uma caixa opaca B. Ômega então vai embora voando, deixando você com a escolha de pegar apenas a caixa B (“uma caixa”) ou pegar a caixa A mais a caixa B (“duas caixas”). Ômega colocou $ 1.000.000 na caixa B se e somente se Ômega previu que você pegaria apenas uma caixa; caso contrário, a caixa B está vazia.

Ômega já partiu; então a caixa B já está vazia ou já está cheia.

Ômega é um excelente previsor do comportamento humano; por exemplo, podemos supor que Ômega tenha sido observado realizando esse experimento 73 vezes e acertando em suas previsões todas as vezes. O problema de Newcomb original estipulava que se você tentasse decidir jogando uma moeda, Ômega deixaria a caixa B vazia; alternativamente, poderíamos supor que Ômega pudesse prever a jogada da moeda.

Você pega ambas as caixas ou apenas a caixa B?

• Argumento 1: as pessoas que pegam apenas a Caixa B tendem a sair ricas. As pessoas que pegam as duas caixas tendem a sair pobres. É melhor ser rico do que pobre.
• Argumento 2: Ômega já fez sua previsão. A Caixa B já está vazia ou já está cheia. Seria irracional deixar para trás a Caixa A sem motivo. É verdade que Ômega escolheu recompensar pessoas com disposições irracionais nesta configuração, mas a Caixa B agora já está vazia, e deixar irracionalmente a Caixa A para trás resultaria apenas factualmente em você receber $0 em vez de $1.000.

O Problema de Newcomb é convencionalmente visto como um exemplo que divide o veredicto entre a teoria evidencial da decisão (“Pegar apenas a Caixa B é uma boa notícia! Faça isso.”) versus a teoria causal da decisão (“Pegar ambas as caixas não faz com que a Caixa B fique vazia, só adiciona $ 1.000 à recompensa”) de uma maneira que inicialmente parece mais favorável aos agentes decisórios evidenciais (que saem ricos).

A configuração do Problema de Newcomb pode parecer forçada, apoiando a acusação de que Ômega está apenas recompensando pessoas com disposições irracionais. Mas considere a seguinte variante, o Caronista de Parfit:

Você está perdido no deserto, sua garrafa de água está quase esgotada, quando alguém para com um caminhão. Este motorista é (a) completamente egoísta e (b) muito bom em detectar mentiras. (Talvez o motorista tenha passado pelo treinamento de Paul Ekman para ler microexpressões faciais.)

O motorista diz que vai levar você até a cidade, mas só se você prometer dar a ele $ 1.000 ao chegar lá.

Se você valoriza sua vida em $ 1.000.000 (paga $1.000 para evitar riscos de morte de 0,1%), então esse problema é quase isomorfo ao Problema de Newcomb transparente de Gary Drescher, no qual a Caixa B é transparente e Ômega colocou $1.000.000 visíveis na Caixa B se e somente se Ômega prevê que você pegará apenas uma caixa ao ver uma Caixa B cheia. Isso torna o Carona de Parfit um problema de tipo Newcomb, mas um em que o comportamento do motorista parece sensato em termos egoístas e não forçado como no caso de Ômega de Newcomb.

Ao chegar à cidade no Caronista de Parfit, você pode ser tentado a raciocinar que o carro já levou você até lá, e então, quando agora você tomar a decisão em seu egoísmo, você vai raciocinar que está em melhor situação em termos de $ 1.000 agora se se recusar a pagar, já que sua decisão não pode alterar o passado. Da mesma forma no Problema de Newcomb transparente; a Caixa B já parece visivelmente cheia, de modo que o dinheiro está ali e não pode desaparecer se você pegar as duas caixas, certo? Mas se você é um tipo de agente que raciocina assim, a Caixa B já está vazia. O motorista de Parfit faz algumas perguntas difíceis e depois parte para deixá-lo morrer no deserto. (Como você conhece seu próprio algoritmo, suas crenças atuais sobre sua decisão futura provavelmente estão fortemente correlacionadas com sua decisão futura; o motorista, que novamente é muito bom em ler rostos, também faz perguntas difíceis como “Você acha que está se enganando?” e “Você está imaginando detalhadamente o cenário no qual já está na cidade?”, ou “Você está planejando secretamente mudar de ideia depois enquanto diz a si mesmo que não está?”)

Tanto os agentes decisórios causais quanto os agentes decisórios evidenciais pegarão as duas caixas na versão transparente do Problema de Newcomb, ou serão deixados para morrer no deserto no Carona de Parfit. Um agente causal que vê uma Caixa B cheia raciocina: “Não posso fazer com que a Caixa B fique vazia deixando a Caixa A para trás.” Um agente evidencial raciocina: “Não seria uma boa notícia sobre nada em particular deixar a Caixa A para trás; eu já sei que a Caixa B está cheia.”

Teoria Lógica da Decisão

A forma mais geral da teoria lógica da decisão, “teoria funcional da decisão”, argumenta que um agente lógico deve calcular a utilidade esperada da seguinte forma:

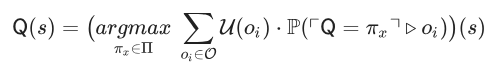
Sendo que:

• Q é o algoritmo de decisão atual do agente, ou seja, todo o cálculo que está sendo executado no momento.
• s são os dados sensoriais do agente.
• π_x é a saída de Q, uma diretriz que mapeia dados sensoriais para ações.
• ⌜Q = π_x⌝ é a proposição de que, como um fato lógico, a saída do algoritmo Q é π_x.
• P(X▹o_i) é a probabilidade de o_i condicionada ao fato lógico X.

A teoria funcional da decisão é formalmente incompleta porque ninguém tem uma especificação completa e formal de como calcular o operador de condicionamento lógico X▹Y. As únicas teorias lógicas da decisão completas são aquelas que calculam casos especiais de X▹Y:

• A teoria da decisão baseada na prova trata X como uma premissa introduzida em um sistema lógico de primeira ordem paradigmático e diz que X▹Y em algum mundo possível se Y pode ser derivado após adicionar a suposição X.
• A teoria atemporal da decisão pressupõe um cenário de decisão na forma de um modelo causal paradigmático ao estilo de Pearl, cujos nós são feitos para denotar proposições lógicas (e particularmente a proposição Q. P( X▹Y ) é então apenas P( Y | do (X)) .

Esses casos especiais são suficientes para:

• Formalizar agentes modais e nos permitir simular formalmente agentes com conhecimento comum do código um do outro negociando no Dilema do Prisioneiro e outras configurações de teoria dos jogos.
• Formalizar o Dilema do Prisioneiro e todos os outros dilemas paradigmáticos, pelo menos até onde a teoria da decisão causal poderia formalizá-los.

Sabemos que esses dois estilos de formalização não são completos porque:

• A teoria da decisão baseada na prova tem casos extremos estranhos indicando que ela só formaliza corretamente a noção intuitiva de condicionamento lógico algumas vezes.
• Não temos um algoritmo geral para construir modelos causais que incluam fatos lógicos, se não estivermos dando-os ao agente como maná dos céus. Também não é óbvio que as regras de probabilidade para modelos causais possam modelar de forma útil correlações lógicas mais complicadas do que “execute exatamente este mesmo algoritmo em dois lugares diferentes”.

Em qualquer configuração que entendemos como representar, um agente decisório lógico alegremente promete pagar os $ 1.000 ao motorista de Parfit (e depois realmente paga). Ele também alegremente deixa para trás a Caixa A no problema original de Newcomb. Um agente decisório lógico está escolhendo a melhor saída para seu algoritmo e raciocinando: “Se meu algoritmo tivesse produzido ‘não pagar’ / ‘pegar ambas as caixas’, então isso teria implicado minha morte no deserto / a Caixa B estar vazia”.

TLD e o Princípio da Escolha Racional

A família geral de teorias lógicas da decisão afirma incorporar o princípio da escolha racional — ou, pelo menos, incorporá-lo melhor do que a teoria causal da decisão ou qualquer alternativa atualmente conhecida. Permanecem problemas em aberto, como uma formulação verdadeiramente geral dos “contrafactuais lógicos” / “condicionamento lógico”. Mas a alegação é que algum tipo de condicionamento à saída lógica do seu algoritmo, em comparação com a clássica teoria causal da decisão, agora parece um candidato muito mais provável para o princípio da escolha racional: ou seja, quando temos um princípio de escolha racional completamente especificado, é muito mais provável que pareça que pertence a alguma parte da família de teorias lógicas da decisão, em vez de pertencer à família de teorias causais da decisão, que pega ambas as caixas no problema de Newcomb.

Alguns dos argumentos apresentados na filosofia da racionalidade incluem:

Argumento da Justiça dos Problemas de Tipo Newcomb

A primeira e principal motivação por trás da TLD é que agentes de TLD sistematicamente acabam ricos. A literatura atual contém ricas linhas de discurso sobre “os que escolhem uma caixa” no Problema de Newcomb perguntando aos que escolhem as duas caixas “Por que tu num tá rico, se tu é tão racional?” e várias respostas do tipo “Não é culpa minha que Ômega decidiu punir pessoas que agiriam racionalmente antes mesmo de eu chegar aqui; isso não muda qual é minha escolha racional agora.”

Essa resposta pode parecer menos persuasiva se estivermos pensando no Caronista de Parfit em vez do Problema de Newcomb. O motorista não está fazendo uma escolha arbitrária e estranha para punir agentes “racionais”. Não faz sentido (egoísta) resgatar alguém que você não prevê que vai pagar depois.

Se no Problema de Newcomb Ômega lesse o código-fonte do agente e decidisse recompensar apenas os agentes com um algoritmo que produzisse “uma caixa” escolhendo a primeira opção em ordem alfabética, punindo todos os agentes que se comportassem exatamente da mesma maneira devido a uma computação interna diferente, então isso seria de fato um torneio tramado. Mas no Problema de Newcomb, Ômega se importa apenas com o comportamento e não com o tipo de algoritmo que o produziu; e um agente pode de fato adotar qualquer tipo de comportamento que desejar; então, de acordo com a TLD, não há motivo para dizer que Ômega está sendo injusto. Você pode fazer a saída lógica do seu algoritmo atual ser o que quiser; então não há motivo para escolher uma saída lógica que o deixe morrer no deserto.

Argumento da Liberdade com relação aos Contrafactuais

Dentro da filosofia analítica, o argumento a favor da teoria causal da decisão repousa principalmente na intuição de que escolher apenas uma caixa no problema de Newcomb não pode fazer com que a Caixa B esteja cheia; ou que no Problema de Newcomb transparente, com a Caixa B transparentemente cheia (ou vazia), não pode ser razoável imaginar que, ao deixar para trás a Caixa A e seus $ 1.000, você possa fazer com que as coisas sejam diferentes.

Não é verdade, em algum sentido, após o motorista de Parfit ter levado o agente de TLD para a cidade no deserto, que no mundo contrafactual em que o agente de TLD não escolhe pagar naquele momento, eles permanecem na cidade? Nesse sentido, um agente de TLD não deve estar iludido sobre alguma questão de fato, ou agir como se estivesse?

O agente de TLD responde:

• Não existem realmente “mundos onde eu não paguei” flutuando por aí. O único mundo real é aquele onde o meu algoritmo de decisão teve a saída que realmente teve. Imaginar outros mundos é um ato de imaginação, computando uma descrição de certo mundo que não existe; não há um mundo correspondente flutuando por aí; então minha descrição dessa impossibilidade não pode ser verdadeira ou falsa sob uma teoria da verdade por correspondência. “Os contrafactuais foram feitos para a humanidade, não a humanidade para os contrafactuais”. Dado isso, posso decidir condicionar às ações que meu algoritmo não realiza da maneira que produz a maior riqueza. Sou livre para dizer “No mundo inexistente onde eu não pago agora, eu já morri no deserto”.
• Eu não escolho apenas uma caixa no Problema de Newcomb porque penso que isso causa fisicamente que a Caixa B esteja cheia. Eu escolho apenas uma caixa no Problema de Newcomb porque calculei isso como a saída ótima de uma maneira completamente diferente. É questionável presumir que um agente racional deva tomar sua decisão realizando algum ritual particular de cognição sobre quais coisas causam fisicamente quais outras coisas; e essa é a premissa por trás da noção de que estou “agindo como se” acreditasse irracionalmente que minha escolha fisicamente causa que a Caixa B esteja cheia.

A esse argumento, o agente de TLD acrescenta que é desejável que os condicionais de ação que calculamos correspondam ao único mundo real. Ou seja, se é um fato que seu algoritmo de decisão produz a ação a_x então sua imaginação do “O mundo onde faço a_x” dentro desse termo da fórmula da utilidade esperada deve corresponder à realidade. Pelo bem do argumento, os agentes de TCD devem violar essa regra ou às vezes entrar em ciclos infinitos.

Argumento da Coerência

Os agentes de TLC nunca precisam recorrer a comprometimentos anteriores (já que os agentes de TLD nunca desejam que seus futuros eus ajam de maneira diferente do algoritmo de TLD). Os agentes de TLD sempre calculam um valor positivo da informação. Por outro lado, p. ex., no Problema de Newcomb transparente, um agente decisório evidencial pode implorar para você não tornar a Caixa B transparente, pois então o agente evidencial escolherá ambas as caixas e, portanto, a Caixa B será revelada como vazia.

Ou similarmente: suponha que, com 10% de probabilidade, Ômega ainda esteja presente e vá encher ou esvaziar a caixa B depois que você fizer sua escolha. Nesse caso, todos os agentes pegam apenas a caixa B (claro!). Agora, suponha que Ômega ainda não tenha configurado o experimento e você não tenha acesso a nenhum meio de comprometimento anterior ou de forçar seu eu futuro a fazer coisa alguma. Eu ameaço revelar se Ômega vai encher ou esvaziar a caixa B antes ou depois do experimento. Como um agente decisório causal, você me pagará milhares de dólares para não revelar essa decisão a você.

Um agente da TCD, tendo a chance de se preparar antes da chegada de Ômega, também pagará uma taxa de $ 10 para ter um assistente de comprometimento anterior por perto com uma arma ameaçando atirar nele se pegar ambas as caixas no Problema de Newcomb. Naturalmente, recebendo a chance de surpresa, o mesmo agente depois (após a partida de Ômega) pagaria $ 10 para fazer o portador da arma ir embora.³

Do ponto de vista da TLD, essas anomalias revelam uma espécie de inconsistência dinâmica ou inconsistência reflexiva na TED e na TCD. Se Ômega está configurando um Problema de Newcomb às 8h, o agente de TCD às 7h e o agente de TCD fazendo a escolha às 9h têm preferências diferentes sobre quantas caixas desejam que o agente de TCD pegue às 9h. O agente de TED no deserto e o agente de TED uma vez que chegou à cidade têm preferências diferentes sobre o que o agente de TED deveria fazer na cidade.

O resultado é que tanto os agentes de TED quanto os agentes de TCD pagarão para forçar seus futuros eus a fazerem coisas, ou alterarão seu próprio código-fonte se puderem. Essa é uma das razões pelas quais a TLD foi originalmente estudada por pesquisadores interessados na teoria dos agentes automodificadores reflexivamente estáveis.

Pode-se, claro, tentar argumentar que todos os problemas de tipo Newcomb são apenas casos especiais estranhos (incluindo votação em eleições?), mas não está claro por que deveríamos fazer isso, considerando que em problemas não de tipo Newcomb, a TED, a TCD e a TLD dão as mesmas respostas. Nesse sentido, a TLD parece dominar, proporcionando um desempenho estritamente melhor na classe de problemas maior e igualmente bom na classe de problemas menor.

Também podemos dizer: “Bem, não há motivo para esperar que o princípio da escolha racional deva ser coerente reflexivamente; quem disse que agentes racionais sempre querem que seus futuros eus sejam racionais?” A literatura da economia moderna considera tão garantidos os “comprometimentos anteriores” e o comportamento “utilmente irracional” na mesa de negociação, que pode parecer estranho afirmar que a consistência dinâmica e a consistência reflexiva são propriedades desejáveis para o princípio da escolha racional ter. Existem apenas dois assuntos de estudo completamente diferentes: o estudo sobre “O que é comportamento racional” e o estudo sobre “Como racionalistas desejam que se comportem” ou racionalidade modificada por comprometimentos prévios, “irracionalidade útil”, “racionalidade social”, “super-racionalidade”, etc.

Mas seria, no entanto, um fato notável se o estudo das “disposições que os agentes racionais desejam ter” apontasse fortemente na direção de um algoritmo geral simples, com propriedades filosoficamente atraentes, que calhasse de ser muito mais autoconsistente de várias maneiras, cujos agentes correspondentes ficassem por aí dizendo coisas como “Por que diabos um agente racional desejaria que seus futuros eus fossem irracionais?” ou “O que você quer dizer com irracionalidade útil? Se um padrão de escolha é útil, não é irracional!”⁴

Um agente decisório causal verdadeiramente puro, sem outros pensamentos além da TCD, descartará todo esse argumento com um suspiro; você não pode alterar o que o Fairbot2 já jogou no Dilema do Prisioneiro e pronto. Mas se nós, humanos reais, nos permitirmos esvaziar nossas mentes de nossos pensamentos anteriores e tentarmos retornar a uma posição intuitiva e pré-teórica, podemos suspeitar ao olhar para essa situação que cometemos um erro sobre o que adotar como nossa teoria explícita da racionalidade.

Consequências Pragmáticas (Visão Geral)

Uma visão geral muito rápida de algumas das consequências pragmáticas da adoção da teoria lógica da decisão:

⚫ O raro livro-texto que entra em detalhes suficientes para apresentar a teoria causal da decisão em vez de apenas usar a formulação errada e simples da utilidade esperada, deve apresentar a equação para a teoria funcional da decisão.

⚫ Vários dilemas econômicos e sociais que envolvem pessoas semelhantes a você, ou pessoas que podem adivinhar como você está pensando, ou pessoas tentando ganhar uma reputação pública por agir de uma certa maneira, levarão a respostas diferentes. Veja, por exemplo, a análise do Jogo do Ultimato como um caso básico para decidir sobre recusar ofertas baixas na mesa de negociação.

⚫ Devemos parar de dizer por aí que dois agentes racionais Desertam um ao outro no Dilema do Prisioneiro. A TLD não é uma panaceia e dois agentes de TLD podem acabar Desertando um ao outro, porque, p. ex., tenho certeza de que você é um agente de TLD, mas não tenho certeza de que você sabe que eu sou um agente de TLD. Mas, p. ex., no Dilema do Prisioneiro Iterado com um horizonte de tempo conhecido, mesmo uma pequena chance de que o outro agente também seja racional em termos de TLD é suficiente para tentar jogar Cooperar na primeira rodada.

⚫ Da mesma forma, podemos parar de dizer por aí que agentes racionais não votam, ou que agentes racionais cedem à chantagem, ou que precisamos de “racionalidade social” em vez de simplesmente racionalidade para que a sociedade tenham coesão, ou que existe esse negócio de ser “utilmente irracional” na mesa de negociação, e assim por diante. A TLD geralmente calcula equilíbrios em dilemas econômicos desse tipo de forma que nunca parece haver uma vantagem visível em ser menos racional.

⚫ Podemos esperar que agentes que conhecem o código um do outro, ou podem calcular os casos prováveis para o código um do outro, sejam extremamente bons em coordenar entre si. Isso pode se aplicar, p. ex., a inteligências artificiais ou a futuras Organizações Autônomas Distribuídas.

⚫ O trabalho futuro em agentes automodificadores deve começar com agentes de TLD em vez de agentes de TCD (ou de TED).

[…]

Notas

1. Na verdade, executamos um pequeno torneio como esse, não só na imaginação.

2. Antes se acreditava ser verdade que “Toxoplasmose faz humanos agirem como gatos”. Mais recentemente, esse resultado pode não ter replicado, infelizmente.

3. Mesmo acreditando que Ômega previu isso com precisão e que a Caixa B está, portanto, vazia!

4. Veja também o episódio de Star Trek no qual Spock fala sobre perder um jogo de xadrez para um oponente que jogou “ilogicamente”.

---

Tradução: Luan Marques

Link para o original