De Denny Zhou, Nathanael Scharli, Le Hou, Jason Wei, Nathan Scales, Xuezhi Wang, Dale Schuurmans, Claire Cui, Olivier Bousquet, Quoc Le, Ed Chi, Google Research, Brain Team. 16 de abril de 2023.
Índice
Resumo
A indução de cadeia de pensamento (chain-of-thought prompting) demonstrou um desempenho notável em várias tarefas de raciocínio em linguagem natural. No entanto, ela tende a ter um desempenho ruim em tarefas que exigem a resolução de problemas mais difíceis do que os exemplares mostrados nos prompts. Para superar esse desafio de generalização de fácil para difícil, propomos uma estratégia de indução inovadora, chamada de indução do mínimo ao máximo (least-to-most prompting). A ideia-chave dessa estratégia é decompor um problema complexo em uma série de subproblemas mais simples e, em seguida, resolvê-los em sequência. A resolução de cada subproblema é facilitada pelas respostas aos subproblemas previamente resolvidos. Nossos resultados experimentais em tarefas relacionadas à manipulação simbólica, generalização composicional e raciocínio matemático revelam que a indução do mínimo ao máximo é capaz de generalizar para problemas mais difíceis do que aqueles vistos nos prompts. Uma descoberta notável é que, quando o modelo GPT-3 code-davinci-002 é usado com a indução do mínimo ao máximo, ele pode resolver o referencial de generalização composicional SCAN em qualquer divisão (incluindo divisão por comprimento) com uma precisão de pelo menos 99%, usando apenas 14 exemplares, em comparação com apenas 16% de precisão com a indução de cadeia de pensamento. Isso é particularmente digno de nota porque os modelos neurossimbólicos na literatura que se especializam em resolver o SCAN são treinados no conjunto de treinamento completo contendo mais de 15.000 exemplos. Incluímos prompts para todas as tarefas no Apêndice.
1. Introdução
Apesar do grande sucesso do aprendizado profundo na última década, ainda existem diferenças enormes entre a inteligência humana e o aprendizado de máquina: (1) ao enfrentar uma nova tarefa, seres humanos geralmente conseguem aprendê-la com apenas alguns exemplos demonstrativos, enquanto o aprendizado de máquina requer uma grande quantidade de dados rotulados para o treinamento do modelo; (2) seres humanos podem explicar claramente a lógica subjacente de suas previsões ou decisões, enquanto o aprendizado de máquina é essencialmente uma caixa-preta; (3) seres humanos podem resolver problemas mais difíceis do que qualquer um que já tenham visto, enquanto para o aprendizado de máquina, os exemplos no treinamento e nos testes são tipicamente do mesmo nível de dificuldade.
A abordagem recentemente proposta da indução de cadeia de pensamento (Wei et al., 2022; Chowdhery et al., 2022) deu um passo significativo para reduzir a lacuna entre a inteligência humana e a inteligência artificial. Ela combina a ideia de raciocínio em linguagem natural (Ling et al., 2017; Cobbe et al., 2021) com a indução de poucas amostras (few-shot prompting) (Brown et al., 2020). Quando integrada ainda mais com decodificação de autoconsistência (Wang et al., 2022b) em vez de usar a típica decodificação gananciosa, a indução de cadeia de pensamento de poucas amostras supera em grande parte os resultados de última geração na literatura em muitas tarefas desafiadoras de processamento de linguagem natural obtidos a partir de modelos neurais especialmente projetados e treinados com centenas de vezes mais exemplos anotados, enquanto é totalmente interpretável.
No entanto, a indução de cadeia de pensamento possui uma limitação fundamental: frequentemente tem um desempenho ruim em tarefas que exigem generalização para resolver problemas mais difíceis do que os exemplos demonstrativos, como a generalização composicional (Lake & Baroni, 2018; Keysers et al., 2020). Para enfrentar essas questões de generalização de fácil para difícil, propomos a indução do mínimo ao máximo. Ela consiste em duas etapas: primeiro, decompor um problema complexo em uma lista de subproblemas mais fáceis e, em seguida, resolver sequencialmente esses subproblemas, sendo que resolver um subproblema dado é facilitado pelas respostas aos subproblemas previamente resolvidos. Ambas as etapas são implementadas por meio da indução de poucas amostras, de modo que não há treinamento ou ajuste fino em nenhuma das etapas. Um exemplo de uso da indução do mínimo ao máximo é ilustrado na Figura 1.
O termo indução do mínimo ao máximo é emprestado da psicologia educacional (Libby et al., 2008), onde é usado para denotar a técnica de usar uma sequência progressiva de induções para ajudar um aluno a aprender uma nova habilidade. Aqui, aplicamos essa técnica para ensinar humanos a ensinar modelos de linguagem. Resultados empíricos em manipulação simbólica, generalização composicional e raciocínio matemático mostram que a indução do mínimo ao máximo pode, de fato, generalizar para problemas mais difíceis do que os demonstrados.
2. Indução do mínimo ao máximo
A indução do mínimo ao máximo ensina modelos de linguagem a resolver um problema complexo decompondo-o em uma série de subproblemas mais simples. Ela consiste em duas etapas sequenciais:
- Decomposição. O prompt nesta etapa contém exemplos constantes que demonstram a decomposição, seguidos pela pergunta específica a ser decomposta.
- Resolução do subproblema. O prompt nesta etapa consiste em três partes: (1) exemplos constantes que demonstram como os subproblemas são resolvidos; (2) uma lista potencialmente vazia de subperguntas anteriormente respondidas e soluções geradas, e (3) a próxima pergunta a ser respondida.
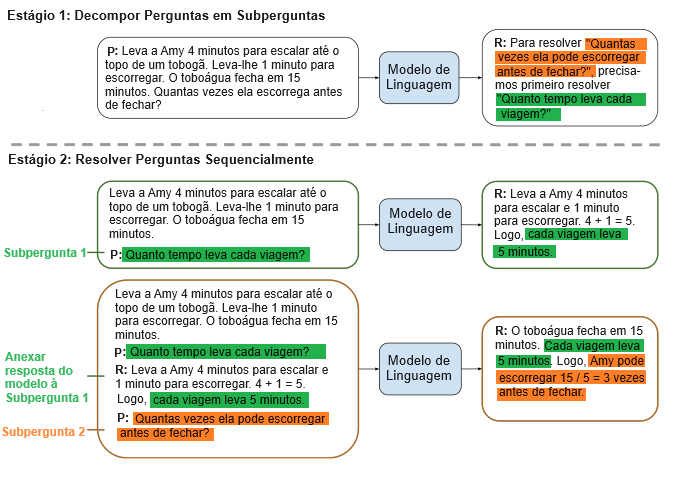
No exemplo mostrado na Figura 1, pede-se primeiro que o modelo de linguagem decomponha o problema original em subproblemas. O prompt que é passado para o modelo consiste em exemplos que ilustram como decompor problemas complexos (que não estão mostrados na figura), seguido pelo problema específico a ser decomposto (como mostrado na figura). O modelo de linguagem descobre que o problema original pode ser resolvido através da resolução de um problema intermediário: “Quanto tempo cada viagem leva?”
Na próxima fase, pedimos ao modelo de linguagem para resolver sequencialmente os subproblemas da etapa de decomposição do problema. O problema original é adicionado como o último subproblema. A resolução começa passando para o modelo de linguagem um prompt que consiste em exemplos que ilustram como os problemas são resolvidos (não mostrados na figura), seguido pelo primeiro subproblema: “Quanto tempo cada viagem leva?” Então, pegamos a resposta gerada pelo modelo de linguagem (“… cada viagem leva 5 minutos.”) e construímos o próximo prompt adicionando a resposta gerada ao prompt anterior, seguido pelo próximo subproblema, que calha de ser o problema original nesse exemplo. O novo prompt é então passado de volta para o modelo de linguagem, que retorna a resposta final.
A indução do mínimo ao máximo pode ser combinada com outras técnicas de indução como a de cadeia de pensamento (Wei et al., 2022) e de autoconsistência (Wang et al., 2022b), mas não precisa ser. Além disso, para algumas tarefas, as duas etapas na indução do mínimo ao máximo podem ser fundidas para formar um prompt de única passagem.
3. Resultados
Apresentamos os resultados da indução do mínimo ao máximo para tarefas de manipulação simbólica, generalização composicional e raciocínio matemático, e comparamos com a indução de cadeia de pensamento.
3.1. Manipulação simbólica
Consideramos a tarefa de concatenação da última letra (Wei et al., 2022). Nesta tarefa, cada entrada é uma lista de palavras, e a saída correspondente é a concatenação das últimas letras das palavras na lista. Por exemplo, “thinking, machine” resulta em “ge”, já que a última letra de “thinking” é “g” e a última letra de “machine” é “e”. A indução de cadeia de pensamento faz um trabalho perfeito quando as listas de testagem têm o mesmo comprimento das listas nos prompts exemplares. No entanto, tem um desempenho ruim quando as listas de testagem são muito mais longas do que as listas nos prompts exemplares. Mostramos que a indução do mínimo ao máximo supera essa limitação e supera significativamente a indução de cadeia de pensamento na generalização do comprimento.
| P: “think, machine, learning” R: “think”, “think, machine”, “think, machine, learning” |
| P: “think, machine” R: A última letra de “think” é “k”. A última letra de “machine” é “e”. Concatenar “k”, “e” leva a “ke”. Logo, “think, machine” produz “ke”. P: “think, machine, learning” R: “think, machine” produz “ke”. A última letra de “learning” é “g”. Concatenar “ke”, “g” leva a “keg”. Logo, “think, machine, learning” produz “keg”. |
Indução do mínimo ao máximo. Os contextos de indução do mínimo ao máximo para a tarefa de concatenação da última letra são mostrados nas Tabelas 1 e 2. O exemplar na Tabela 1 demonstra como decompor uma lista em uma sequência de sublistas. O exemplar na Tabela 2 demonstra como mapear uma entrada para a saída desejada. Dada uma nova lista, primeiro a adicionamos ao exemplar na Tabela 1 para construir o prompt de decomposição, que é enviado ao modelo de linguagem para obter a decomposição da lista. Em seguida, construímos para cada sublista S um prompt de solução, que consiste nos exemplares na Tabela 2, seguidos pelos pares de sublistas/respostas anteriores (se houver), seguidos por S. Emitimos sequencialmente esses prompts para o modelo de linguagem e usamos a última resposta como solução final.
Vale a pena dar uma olhada mais de perto nos exemplares na Tabela 2. Basicamente, eles ensinam modelos de linguagem a construir respostas para novos problemas usando as respostas para problemas anteriormente resolvidos: (1) a lista no segundo exemplar (“think, machine, learning”) é uma extensão da lista no primeiro exemplar (“think, machine”), em vez de uma completamente independente; (2) a resposta para “think, machine, learning” é construída a partir da saída de “think, machine” começando com uma frase dizendo que “think, machine” produz “ke”. Os dois exemplares juntos ilustram um caso-base e uma etapa recursiva.
Indução de cadeia de pensamento. O contexto da indução de cadeia de pensamento para a tarefa de concatenação da última letra está listado na Tabela 3. Ele usa as mesmas listas que a indução do mínimo ao máximo na Tabela 2. A única diferença é que, na indução de cadeia de pensamento, a resposta à segunda lista (“think, machine, learning”) é construída do zero, em vez de usar a saída da primeira lista (“think, machine”).
| P: “think, machine” R: A última letra de “think” é “k”. A última letra de “machine” é “e”. Concatenar “k”, “e” leva a “ke”. Logo, “think, machine” produz “ke”. P: “think, machine, learning” R: A última letra de “think” é “k”. A última letra de “machine” é “e”. A última letra de “learning” é “g”. Concatenar “k”, “e”, “g” leva a “keg”. Logo, “think, machine, learning” produz“keg”. |
Comparamos a indução do mínimo ao máximo (Tabela 1 e 2) com a indução de cadeia de pensamento (Tabela 3) e a indução-padrão de poucas amostras. O prompt para a indução-padrão de poucas amostras é construído removendo as explicações intermediárias na indução de cadeia de pensamento. Ou seja, ele consiste apenas nesses dois exemplares: (1) “think, machine” produz “ke”; e (2) “think, machine, learning” produz “keg”. Não consideramos uma linha de base de treinamento ou ajuste fino porque um modelo de aprendizado de máquina baseado em dois exemplares generalizaria muito mal.
Resultados. Retiramos como amostras aleatórias palavras no Wikcionário 1 para construir listas de testagem com comprimentos variando de 4 a 12. Para cada comprimento dado, são construídas 500 listas. As precisões de diferentes métodos com code-davinci-002 no GPT-3 são mostradas na Tabela 4. A indução-padrão falha completamente em todos os casos de teste com uma precisão de 0. A indução de cadeia de pensamento aumenta significativamente o desempenho com relação à indução-padrão, mas ainda fica bem atrás da indução do mínimo ao máximo, especialmente quando as listas são longas. Além disso, o desempenho da indução de cadeia de pensamento cai muito mais rápido do que a indução do mínimo ao máximo à medida que o comprimento aumenta.
| L = 4 | L = 6 | L = 8 | L = 10 | L = 12 | |
| Indução-padrão | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| Cadeia de pensamento | 84,2 | 69,2 | 50,2 | 39,8 | 31,8 |
| Mínimo ao máximo | 94,0 | 88,4 | 83,0 | 76,4 | 74,0 |
Nos Apêndices 7.2 e 7.3, apresentamos experimentos adicionais com diferentes prompts de cadeia de pensamento e diferentes modelos de linguagem. Note que, ao contrário da indução do mínimo ao máximo, os exemplares em um prompt de cadeia de pensamento podem ser independentes entre si. Para a tarefa de concatenação da última letra, isso significa que não precisamos apresentar exemplares que sejam sublistas de outros exemplares. Na verdade, um prompt de cadeia de pensamento com listas independentes tende a ter um desempenho melhor do que um com listas dependentes, já que o primeiro transmite mais informações. Além disso, podemos melhorar a indução de cadeia de pensamento incorporando exemplares adicionais. Isso parece ser justo, já que a indução do mínimo ao máximo contém mais palavras devido à sua decomposição extra. Conforme mostrado na Tabela 13 (Apêndice 7.3), para listas com comprimento 12, a indução de cadeia de pensamento alcança uma precisão de 37,4% com 4 exemplares independentes (Apêndice 7.2.2) e 38,4% com 8 exemplares independentes (Apêndice 7.2.3). Embora tenha havido avanços notáveis em comparação com uma precisão de 31,8% do prompt original na Tabela 3, a indução de cadeia de pensamento ainda fica atrás da indução do mínimo ao máximo, que ostenta uma precisão de 74,0%.
Análise de erros. Embora a indução do mínimo ao máximo supere significativamente a indução de cadeia de pensamento, ainda está longe de alcançar 100% de precisão para listas longas. No Apêndice 7.4, apresentamos uma análise detalhada de erros. Descobrimos que apenas alguns deles são devidos a letras finais incorretas, enquanto a maioria são erros de concatenação (eliminar ou adicionar uma letra). Por exemplo, dada a lista “gratified, contract, fortitude, blew”, o modelo elimina a última letra na concatenação de “dte” e “w”, e assim prevê o resultado como sendo “dte” em vez de “dtew”. Em outro exemplo “hollow, supplies, function, gorgeous”, o modelo de alguma forma duplica a última letra “s” na concatenação de “wsn” e “s”, e assim a previsão se torna “wsnss” em vez de “wsns”.
Referências
Consulte as referências do documento original.
Notas
1. https://en.wiktionary.org/wiki/Wiktionary:Frequency_lists/PG/2006/04/1-10000
Tradução: Luan Marques
Link para o original
