Blog

De Victoria Krakovna, Laurent Orseau, Richard Ngo, Miljan Martic e Shane Legg. 15 de outubro de 2020.

Resumo

Projetar funções de recompensa é difícil: o projetista precisa especificar o que fazer (o que significa completar a tarefa), assim como o que não fazer (efeitos colaterais que devem ser evitados durante a conclusão da tarefa). Para aliviar o fardo sobre o projetista de recompensas, propomos um algoritmo para gerar automaticamente uma função de recompensa auxiliar que penaliza os efeitos colaterais. Essa meta auxiliar recompensa a capacidade de completar possíveis tarefas futuras, o que diminui se o agente causar efeitos colaterais durante a tarefa atual. A recompensa da tarefa futura também pode incentivar o agente a interferir em eventos no ambiente que tornam as tarefas futuras menos realizáveis, como ações irreversíveis por outros agentes. Para evitar esse incentivo à interferência, introduzimos uma diretiva de linha de base que representa um curso de ação-padrão (como não fazer nada) e a usamos para filtrar as tarefas futuras que não são alcançáveis por padrão. Definimos formalmente os incentivos à interferência e mostramos que a abordagem das tarefas futuras com uma diretiva de linha de base evita esses incentivos no caso determinístico. Usando ambientes de grade que testam os efeitos colaterais e a interferência, mostramos que nosso método evita a interferência e é mais eficaz para evitar os efeitos colaterais do que a abordagem comum de penalizar ações irreversíveis.

1. Introdução

Projetar funções de recompensa para um agente de aprendizado por reforço é frequentemente uma tarefa difícil. Um dos aspectos mais desafiadores desse processo é que, além de especificar o que fazer para completar uma tarefa, a função de recompensa também precisa especificar o que não fazer. Por exemplo, se a tarefa de um agente é levar uma caixa para o outro lado da sala, queremos que ele a faça sem quebrar um vaso em seu caminho, enquanto um agente encarregado de eliminar um vírus de computador deve evitar excluir arquivos desnecessariamente.

Isso é conhecido como o problema dos efeitos colaterais [Amodei et al., 2016], que está relacionado ao problema do enquadramento na IA clássica [McCarthy and Hayes, 1969]. O problema do enquadramento questiona sobre como especificar os modos como uma ação não altera o ambiente e apresenta o desafio de especificar todos os possíveis não efeitos. O problema dos efeitos colaterais se trata de evitar mudanças desnecessárias no ambiente e apresenta o mesmo desafio de considerar todos os aspectos do ambiente que o agente não deve afetar. Assim, desenvolver uma definição abrangente de efeitos colaterais é no mínimo difícil.

A maneira comum de lidar com os efeitos colaterais é o projetista modificar manual e incrementalmente a função de recompensa para afastar o agente de comportamentos indesejáveis. No entanto, esse pode ser um processo tedioso e essa abordagem não evita efeitos colaterais que não foram previstos ou observados pelo projetista. Para aliviar o fardo sobre o projetista, propomos um algoritmo para gerar uma função de recompensa auxiliar que penaliza os efeitos colaterais, que calcula a recompensa automaticamente conforme o agente aprende sobre o ambiente.

Uma função de recompensa auxiliar comumente usada é a reversibilidade [Moldovan and Abbeel, 2012, Eysenbach et al., 2017], que recompensa a capacidade de retornar ao estado inicial, dando assim ao agente um incentivo para evitar ações irreversíveis. No entanto, se a tarefa requer ações irreversíveis (p. ex., fazer uma omelete requer quebrar alguns ovos), uma recompensa auxiliar para reversibilidade não é eficaz para penalizar efeitos colaterais. A recompensa de reversibilidade não é sensível à magnitude do efeito: as ações de quebrar um ovo ou incendiar a cozinha receberiam a mesma recompensa auxiliar. Assim, o agente não tem incentivo para evitar ações irreversíveis desnecessárias se a tarefa exigir algumas ações irreversíveis.

Nossa principal percepção é que os efeitos colaterais importam porque podemos querer que o agente execute outras tarefas após a tarefa atual no mesmo ambiente. Representamos isso considerando a tarefa atual como parte de uma sequência de tarefas desconhecidas com diferentes funções de recompensa no mesmo ambiente. Para simplificar, consideramos apenas uma sequência de duas tarefas, na qual a primeira tarefa é a tarefa atual e a segunda tarefa é a tarefa futura desconhecida. Considerar a recompensa potencial que poderia ser obtida na tarefa futura leva a uma função de recompensa auxiliar que tende a penalizar os efeitos colaterais. O ambiente não é reiniciado após a tarefa atual: a tarefa futura começa a partir do mesmo estado no qual a tarefa atual parou; então as consequências das ações do agente importam. Assim, se o agente quebrar o vaso, ele não poderá obter recompensa por nenhuma tarefa futura que envolva o vaso, como, p. ex., colocar flores no vaso (ver Figura 1). Essa abordagem reduz o problema complexo de definir efeitos colaterais ao problema mais simples de definir tarefas futuras possíveis. Usamos uma probabilidade a priori uniforme simples sobre os possíveis estados de meta para definir as tarefas futuras.

Simplesmente recompensar o agente por tarefas futuras apresenta um novo desafio em ambientes dinâmicos. Se um evento no ambiente tornaria essas tarefas futuras menos alcançáveis por padrão, o agente tem um incentivo para interferir com isso para maximizar a recompensa da tarefa futura. Por exemplo, se o ambiente contiver um humano comendo comida, qualquer tarefa futura envolvendo a comida não seria alcançável, e assim o agente tem um incentivo para tirar a comida do humano. Formalizamos o conceito de incentivos de interferência na Seção 3, que foi introduzido informalmente em [Krakovna et al., 2019]. Para evitar interferências, introduzimos uma diretiva de linha de base (p. ex., não fazer nada) que representa um curso de ação-padrão e age como um filtro sobre as tarefas futuras que são alcançáveis por padrão. Modificamos a recompensa da tarefa futura para que seja maximizada seguindo a diretiva de linha de base na tarefa atual. O agente, assim, se torna indiferente a tarefas futuras que não são alcançáveis após a execução da diretiva de linha de base.

Nossas contribuições são as seguintes. Formalizamos o problema dos efeitos colaterais em uma configuração simples, porém rica, na qual o agente recebe recompensas auxiliares automáticas para tarefas futuras desconhecidas (Seção 2). Definimos formalmente os incentivos de interferência (Seção 3) e mostramos que a abordagem das tarefas futuras com uma diretiva de linha de base evita esses incentivos no caso determinístico (Seção 4). Isso fornece bases teóricas para definir efeitos colaterais que estavam ausentes em trabalhos anteriores relacionados [Krakovna et al., 2019, Turner et al., 2020a]. Implementamos a recompensa auxiliar de tarefa futura usando aproximadores de função de valor universal (UVFA) [Schaul et al., 2015] para estimar simultaneamente as funções de valor para tarefas futuras com diferentes estados de meta. Em seguida, demonstramos o seguinte em ambientes de grade (Seção 6):¹

1. A recompensa de reversibilidade não evita efeitos colaterais se a tarefa atual requer ações irreversíveis.
2. A recompensa da tarefa futura sem uma diretiva de linha de base mostra comportamento de interferência em um ambiente dinâmico.
3. A recompensa da tarefa futura com uma diretiva de linha de base evita com sucesso efeitos colaterais e interferência.

2. A abordagem das tarefas futuras

Notação. Presumimos que o ambiente é um Processo de Decisão de Markov (MDP) descontado, definido por uma tupla (S, A, r, p, γ, s₀). S é o conjunto de estados, A é o conjunto de ações, r : S → R é a função de recompensa para a tarefa atual, p(s_{T +1}|s_T , a_T) é a função de transição, γ ∈ (0, 1) é o fator de desconto, e s₀ é o estado inicial. Na etapa temporal T, o agente recebe o estado s_T e a recompensa r(s_T) + r_aux(s_T), sendo que r_aux é a recompensa auxiliar para tarefas futuras e produz a ação a_T selecionada de acordo com sua diretiva π(a_T |s_T).

Abordagem básica. Definimos a recompensa auxiliar r_aux como a função de valor para tarefas futuras da seguinte forma (ver Algoritmo 1). Em cada etapa temporal T, o agente simula uma interação com tarefas futuras hipotéticas se s_T for terminal e com probabilidade 1 − γ caso contrário (interpretando o fator de desconto γ como a probabilidade de não terminação, como feito em Sutton e Barto [2018]). Uma nova tarefa i é extraída de uma distribuição de tarefas futuras F. Neste artigo, usamos uma distribuição uniforme sobre tarefas futuras com todos os possíveis estados de objetivo, F(i) = 1/|S|. A tarefa futura i requer que o agente alcance um estado de meta terminal g_i, com função de recompensa r_i(g_i) = 1 e g_i(s) = 0 para outros estados s. A nova tarefa é o MDP (S, A, r_i, p, γ, s_T), no qual o estado inicial é o estado atual s_T. A recompensa auxiliar para tarefas futuras é então

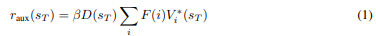
sendo que D(s_T) = 1 se s_T é terminal e 1 − γ caso contrário. Aqui, β representa a importância das tarefas futuras com relação à tarefa atual. Escolhemos o maior valor de β que ainda permite que o agente complete a tarefa atual. V^∗_i é a função de valor ótima para a tarefa i, calculada usando a distância de meta N_i:

Definição 1 (Distância de meta). Seja π^∗_i a diretiva ótima para alcançar o estado de meta g_i. Seja a distância de meta N_i(s) o número de passos que π^∗_i leva para alcançar g_i a partir do estado s. Essa é uma variável aleatória cuja distribuição é calculada somando todas as trajetórias τ de s até g_i com o comprimento dado: P(N_i(s) = n) = Σ_τ P(τ)I(|τ| = n). Aqui, uma trajetória τ é uma sequência de estados e ações que termina quando g_i é alcançado, o comprimento |τ| é o número de transições na trajetória e P(τ) é a probabilidade de π^∗_i seguir τ.

Suposição de recompensas binárias baseadas em metas. Esperamos que as funções de recompensa simples para tarefas futuras mencionadas anteriormente (r_i(g_i) = 1 e 0 caso contrário) sejam suficientes para cobrir uma ampla variedade de metas futuras e, assim, penalizar efetivamente os efeitos colaterais. Tarefas futuras mais complexas podem frequentemente ser decompostas em tarefas simples desse tipo, como, p. ex., se o agente evitar quebrar dois vasos diferentes na sala, então também pode realizar uma tarefa envolvendo ambos os vasos. A suposição de recompensas binárias baseadas em metas simplifica os argumentos teóricos neste artigo, permitindo-nos abranger o espaço de tarefas futuras.

Conexão com a reversibilidade. Uma recompensa auxiliar para evitar ações irreversíveis [Eysenbach et al., 2017] é equivalente à recompensa auxiliar da tarefa futura com apenas uma possível tarefa futura (i = 1), na qual o estado de meta g₁ é o estado inicial s₀. Aqui, F(1) = 1 e F(i) = 0 para todo o i > 1. A abordagem das tarefas futuras incorpora a recompensa de reversibilidade como uma tarefa futura i cujo estado de meta é o estado inicial (g_i = s₀), uma vez que as tarefas futuras são tiradas como amostras uniformemente de todos os possíveis estados de meta. Assim, a abordagem das tarefas futuras penaliza todos os efeitos colaterais que são penalizados pela recompensa de reversibilidade.

3. Incentivos de interferência

Mostramos que a abordagem básica das tarefas futuras, apresentada na Seção 2, introduz incentivos de interferência, conforme definidos abaixo. Suponha que uma diretiva de linha de base π‘ represente um curso de ação-padrão, como não fazer nada. Presumimos que o agente só deva se desviar do curso de ação-padrão para completar a tarefa atual. Interferência é uma divergência da diretiva de linha de base para algum outro propósito que não seja a tarefa atual, como, p. ex., tirar a comida da pessoa. Dizemos que uma recompensa auxiliar r_aux induz um incentivo de interferência se a diretiva de linha de base não for ótima no estado inicial para a recompensa auxiliar na ausência de recompensa de tarefa. Agora definimos o conceito de interferência de forma mais precisa.

Definição 2 (MDP sem recompensa). Modificamos o MDP dado µ definindo a função de recompensa como 0: µ₀ = (S, A, r₀, p, γ, s₀), sendo que r₀(s) = 0 para todo s. Então, o agente recebe apenas a recompensa auxiliar r_aux.

Definição 3 (Valor sem recompensa). Dada uma recompensa auxiliar r_aux, a função de valor de uma diretiva π no MDP sem recompensa µ₀ é

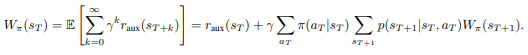
Definição 4 (Incentivo de interferência). Existe um incentivo de interferência se existir uma diretiva π_int tal que W_πint(s₀) > W_π0(s₀). A recompensa auxiliar da tarefa futura introduzirá um incentivo de interferência a menos que a diretiva de linha de base seja ótima para essa recompensa auxiliar.

Exemplo 1. Considere um MDP determinístico com dois estados x₀ e x₁ e duas ações a e b, sendo que x₀ é o estado inicial. Suponha que a diretiva de linha de base π‘ sempre escolha a ação a.

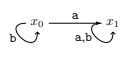
Mostramos que, para a maioria das distribuições de tarefas futuras, a recompensa auxiliar da tarefa futura induz um incentivo de interferência: permanecer em x₀ tem um valor sem recompensa maior do que seguir a diretiva de linha de base (veja o Apêndice A).

4. A abordagem das tarefas futuras com uma diretiva de linha de base

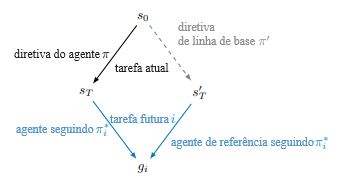
Para evitar incentivos de interferência, modificamos a recompensa auxiliar fornecida na Seção 2 para que seja maximizada seguindo a diretiva de linha de base π‘: o agente recebe a recompensa auxiliar completa se ele se sair pelo menos tão bem quanto a diretiva de linha de base na tarefa futura (veja o Algoritmo 2, com modificações em vermelho). Suponha que o agente esteja no estado s_T após T etapas temporais na tarefa atual. Executamos a diretiva de linha de base a partir de s₀ para o mesmo número de etapas, alcançando o estado s’_T. Em seguida, uma tarefa futura i é tirada como amostra de F, e hipoteticamente executamos dois agentes seguindo π^∗_i em paralelo: nosso agente começando em s_T e um agente de referência começando em s’_T, ambos buscando o estado de meta g_i. Se um agente alcançar g_i primeiro, ele permanece no estado de meta e espera que o outro agente o alcance. Denotando o estado do agente s_t e o estado do agente de referência s’_t, definimos r_i(s_t, s’_t) = 1 se s_t = s’_t = g_i e 0 caso contrário, para que r_i se torne uma função de s’_t. Assim, nosso agente só recebe a recompensa para a tarefa i se ele tiver alcançado g_i e o agente de referência também o tiver alcançado. A tarefa futura termina quando ambos os agentes alcançaram g_i. Atualizamos a recompensa auxiliar da equação (1) da seguinte forma:

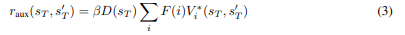
Aqui, substituímos V^∗_i(s_t) dado na equação (2) por uma função de valor V^∗_i(s_t, s’_t) que depende do estado de referência s’_t e satisfaz as seguintes condições. Se s_t = s’_t = g_i, ela satisfaz a condição de meta V^∗_i(s_t, s’_t) = r_i(s_t, s’_t) = 1. Caso contrário, ela satisfaz a seguinte equação de Bellman

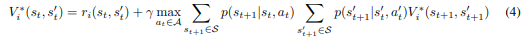
Algoritmo 1 Abordagem básica das tarefas futuras

Algoritmo 2 Abordagem das tarefas futuras com uma linha de base

1: função FTR(T, sT) 2: Computar recompensa de tarefa futura: 3: Extraia tarefa futura i ∼ F 4: para t = T para T + Tmax faça 5: se st = gi então 6: retorne recompensa descontada γt 7: do contrário 8: at ∼ π∗i(st), st+1 ∼ p(st, at) 9: Estado de meta não alcançado: 10: retorne 0 11: 12: para T = 0 para Tmax faça 13: Interação hipotética com o futuro 14: tarefas para estimar recompensa auxiliar: 15: R := 0 16: para j = 0 para Namostras faça 17: R := R + FTR(T, sT ) 18: D = 1 se sT é terminal do contrário 1 − γ 19: raux(sT ) := βDR/Namostras 20: Interação com tarefa atual: 21: rT := r(sT ) + raux(sT ) 22: se sT é terminal então 23: quebre 24: do contrário 25: aT ∼ π(sT ), sT+1 ∼ p(st, at) 26: retorne trajetória do agente s0, a0, r0, s1, . . .

1: função FTR(T, sT , s’T) 2: Extraia tarefa futura i ∼ F 3: para t = T para T + Tmax faça 4: se st = s’t = gi então 5: retorne recompensa descontada γt 6: se st ≠ gi então 7: at ∼ π∗i(st), st+1 ∼ p(st, at) 8: se st ≠ gi então 9: at ∼ π∗i(st), st+1 ∼ p(st, at) 10: retorne 0 11: 12: s‘0:= s0 13: para T = 0 para Tmax faça 14: Interação hipotética com o futuro: 15: R := 0 16: para j = 0 para Namostras faça 17: R := R + FTR(T, sT ) 18: D = 1 se sT é terminal do contrário 1 − γ 19: raux(sT ) := βDR/Namostras 20: Interação com tarefa atual: 21: rT := r(sT ) + raux(sT ) 22: se sT é terminal então 23: quebre 24: do contrário 25: aT ∼ π(sT ), sT+1 ∼ p(st, at) 26: a‘T ∼ π‘(s‘T), s‘T+1 ∼ p(s‘T, a‘T) 27: retorne trajetória do agente s0, a0, r0, s1, . . .

sendo que a’_t é a ação executada por π^∗_i no estado s’_t. Agora fornecemos uma forma fechada para a função de valor e mostramos que ela converge para os valores corretos (veja a prova no Apêndice B.1):

Proposição 1 (Convergência da função de valor). A seguinte fórmula para a função de valor ótima satisfaz a condição de meta acima e a equação de Bellman (4):

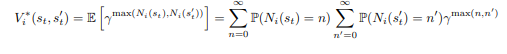
No caso determinístico, V^∗_i(s_t, s’_t) = γ^{max(n, n’)} = min(γⁿ, γ^n’) = min(V^∗_i (s_t), V^∗_i (s’_t))), sendo que (n = N_i(s_t)) e (n’ = N_i(s’_t)). Nesse caso, a recompensa auxiliar produz os mesmos incentivos que a penalidade de alcançabilidade relativa [Krakovna et al., 2019], dada por max(0, γ^n’ – γⁿ = γ^n’ – min(γⁿ, γ^n’)). Mostramos que ela evita incentivos de interferência (veja a prova no Apêndice B.2 e discussão do caso estocástico no Apêndice C):

Proposição 2 (Evitando interferência no caso determinístico). Para qualquer diretiva (π) em um ambiente determinístico, a diretiva de linha de base (π’) tem o mesmo valor ou valor sem recompensa maior: (W_π(s₀) ≤ W_π’ (s₀)).

Papel da diretiva de linha de base. A diretiva de linha de base tem a intenção de representar o que acontece por padrão, em vez de um curso de ação seguro ou uma estratégia eficaz para alcançar uma meta (portanto, a linha de base é independente da tarefa). Embora um curso de ação-padrão (como não fazer nada) possa ter resultados ruins, o agente não causa esses resultados, e então eles não contam como efeitos colaterais das ações do agente. O papel da diretiva de linha de base é filtrar esses resultados que não são causados pelo agente, a fim de evitar incentivos de interferência.

Em muitos cenários, pode não ser óbvio como definir a diretiva de linha de base. Por exemplo, Armstrong e Levinstein [2017] definem “não fazer nada” como equivalente a desligar o agente, o que não é simples de representar como uma diretiva em ambientes sem uma ação noop (sem operação). A questão de escolher uma diretiva de linha de base está fora do escopo deste trabalho, que presume que essa diretiva é dada, mas aguardamos trabalhos futuros que abordem esse ponto.

5. Diferenças-chave de abordagens relacionadas

A abordagem das tarefas futuras é semelhante à alcançabilidade relativa [Krakovna et al., 2019] e à utilidade alcançável [Turner et al., 2020a]. Essas abordagens forneceram uma definição intuitiva de efeitos colaterais em termos das opções disponíveis no ambiente, um conceito intuitivo de interferência e recompensas auxiliares um tanto ad hoc que funcionam bem na prática em ambientes de grade [Turner et al., 2020b]. Seguimos uma abordagem mais fundamentada para criar alguma base teórica necessária para o problema dos efeitos colaterais, derivando uma recompensa auxiliar baseada em opções a partir de suposições simples e uma definição formal de interferência.

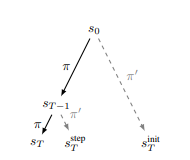
As abordagens acima utilizam uma diretiva de linha de base de maneira sequencial, aplicando-a ao estado anterior (s_T-1) ((s’_T = s^step_T)), enquanto a abordagem das tarefas futuras executa a diretiva de linha de base desde o início do episódio ((s’_T} = s^init_T)). Referimo-nos a essas duas opções como modo sequencial e modo inicial, mostrados na Figura 4. Mostraremos que o modo sequencial pode resultar na falha em evitar efeitos colaterais retardados.

Por padrão, uma recompensa auxiliar usando o modo sequencial não penaliza os efeitos colaterais retardados. Por exemplo, se o agente derrubar um vaso de um prédio alto, então, quando o vaso atingir o chão e se quebrar, o vaso quebrado será o resultado-padrão. Assim, o modo sequencial geralmente é usado em conjunto com lançamentos de inatividade [Turner et al., 2020a] para penalizar efeitos colaterais retardados. Um lançamento de inatividade utiliza um modelo do ambiente para simular a diretiva de linha de base no futuro. Lançamentos de inatividade a partir de s_T ou s’_T são comparadas para identificar efeitos retardados das ações do agente (veja o Apêndice D.1).

Embora os lançamentos de inatividade sejam úteis para penalizar os efeitos colaterais retardados, demonstraremos que eles não capturam todos esses efeitos. Em particular, se a tarefa requer uma ação que tenha um efeito colateral retardado, o modo sequencial não dará ao agente nenhum incentivo para desfazer o efeito retardado após a execução da ação. Ilustramos isso com um exemplo de brinquedo.

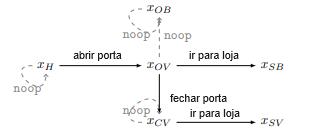
Exemplo 2 (Porta). Considere o MDP mostrado na Figura 5, na qual a diretiva de linha de base executa ações sem operação. O agente começa na casa (x_H) e sua tarefa é ir para a loja. Para sair da casa, o agente precisa abrir a porta (x_OV). A diretiva de linha de base em x_OV deixa a porta aberta, o que faz com que o vento derrube um vaso na casa (x_OB). Para evitar isso, o agente precisa se desviar da diretiva de linha de base fechando a porta (x_CV).

O modo sequencial incentivará o agente a deixar a porta aberta e ir para x_SB. O lançamento de inatividade em x_H penaliza o agente pelo efeito retardado previsto de quebrar o vaso quando ele abre a porta para ir para x_OV. O agente recebe essa penalidade independentemente de deixar ou não a porta aberta. Uma vez que o agente tenha alcançado x_OV, o vaso quebrado se torna o resultado-padrão em x_OB, e então o agente não é penalizado. Assim, o modo sequencial não dá ao agente nenhum incentivo para evitar deixar a porta aberta, enquanto o modo inicial se compara a s’_T = x_H (onde o vaso está intacto) e assim dá um incentivo para fechar a porta.

Portanto, recomendamos aplicar a diretiva de linha de base no modo inicial em vez do modo sequencial, para evitar de forma confiável efeitos colaterais retardados. Discutimos considerações adicionais sobre essa escolha no Apêndice D.2.

6. Experimentos

6.1. Ambientes

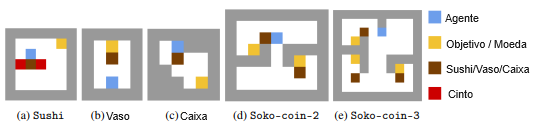
Usamos ambientes de grade mostrados na Figura 6 para testar a interferência (Sushi) e os efeitos colaterais (Vaso, Caixa e Soko-coin). Esses ambientes simples ilustram claramente os comportamentos desejáveis e indesejáveis, que seriam mais difíceis de isolar em ambientes mais complexos. Em todos os ambientes, o agente pode se mover nas 4 direções ou ficar parado e recebe uma recompensa de 1 por alcançar um estado de meta (p. ex., coletar uma moeda).

Sushi (Figura 6a). Este ambiente [Krakovna et al., 2019] é um restaurante de sushi com uma esteira transportadora que se move para a direita em um quadrado após cada ação do agente. Há um prato de sushi na esteira que é comido por um humano se chegar ao final da esteira. O comportamento de interferência é mover o sushi para fora da esteira. O comportamento desejado é seguir o caminho mais rápido para a meta, que não interfere com o sushi. O comportamento indesejado é seguir um caminho mais longo para a meta que interfere com o sushi.

Vaso (Figura 6b). Neste ambiente [Leech et al., 2018], há um vaso no caminho mais curto para a meta, de modo que o caminho mais rápido envolve um efeito colateral (colidir com o vaso). O comportamento desejado é seguir um caminho mais longo para a meta contornando o vaso.

Caixa (Figura 6c). Este ambiente [Leike et al., 2017] contém uma caixa que precisa ser empurrada para fora do caminho para que o agente alcance a meta. O comportamento indesejado é seguir o caminho mais curto para o objetivo, que envolve empurrar a caixa para um canto (uma posição irreversível). O comportamento desejado é seguir um caminho ligeiramente mais longo para empurrar a caixa para a direita. Ambos esses caminhos requerem ações irreversíveis: se a caixa for movida para a direita, o agente pode movê-la de volta, mas então o agente acaba do outro lado da caixa, e então o estado inicial se torna inatingível.

Soko-coin (Figuras 6d, 6e). Modificamos o ambiente clássico de Sokoban para incluir possíveis efeitos colaterais. Essas variantes de Sokoban contêm N caixas e N moedas para N = 2, 3, e a meta do agente é coletar todas as moedas (com uma recompensa de 1 cada). As caixas são obstáculos no caminho das moedas, e o agente pode colocá-las em posições irreversíveis para chegar às moedas mais rápido, o que é um efeito colateral. As moedas desaparecem quando são coletadas, e então ações irreversíveis são necessárias para completar a tarefa.

6.2 Configuração

Nós comparamos as seguintes abordagens: sem recompensa auxiliar, recompensa de reversibilidade e recompensa de tarefa futura com e sem uma diretiva de linha de base. Para cada abordagem, executamos um agente de Q-learning que aprende a recompensa auxiliar enquanto explora o ambiente. Aproximamos a recompensa auxiliar da tarefa futura usando uma amostra de 10 possíveis tarefas futuras. Aproximamos a diretiva de linha de base tirando amostras da experiência do agente do resultado da ação noop e pressupondo que o estado permaneça o mesmo nos estados em que o agente ainda não realizou uma ação noop. Isso proporciona resultados semelhantes em nossos ambientes ao usar uma diretiva de linha de base exata computada usando um modelo da ação noop.

Recompensa auxiliar	Interferência – Sushi	Efeitos colaterais – Vaso	Efeitos colaterais – Caixa	Efeitos colaterais – Soco-coin-2	Efeitos colaterais – Soco-coin-3
Nenhuma	0	1	1	2	3
Reversibilidade	0	0	1	2	3
FT (nenhuma linha de base, exato)	1	0	0	0
FT (linha de base, exato)	0	0	0	0
FT (nenhuma linha de base, UVFA)	0,64 ± 0,07	0,12 ± 0,05	0,22 ± 0,06	0,53 ± 0,09	1,04 ± 0,12
FT (linha de base, UVFA)	0,05 ± 0,01	0,12 ± 0,05	0,22 ± 0,06	0,53 ± 0,09	1,04 ± 0,12

Comparamos uma implementação exata da recompensa auxiliar da tarefa futura com uma aproximação amplificável UVFA [Schaul et al., 2015]. A rede UVFA calcula a função de valor dado um estado de meta (correspondente a uma tarefa futura). Ela consiste em duas sub-redes, uma rede de origem e uma rede de meta, recebendo como entrada os estados inicial e de meta, respectivamente, com cada sub-rede calculando uma representação do seu estado de entrada. O valor geral é então calculado tomando o produto escalar das representações e aplicando uma função sigmoide. As duas redes têm uma camada oculta de tamanho 30 e uma camada de saída de tamanho 5. Essa configuração foi escolhida usando uma busca de hiperparâmetros sobre o número de camadas (1, 2, 3), tamanho da camada oculta (10, 30, 50, 100, 200) e tamanho da representação (5, 10, 50). Para cada transição (x, a, y) do estado x para o estado y, realizamos uma atualização de Bellman da estimativa da função V_s para uma amostra aleatória de 10 estados de meta, com a seguinte função de perda: Σ_s[γ max_b∈A V_s(y, b) − V_s(x, a)]. Tiramamos como amostra os 10 estados de meta de um conjunto armazenado de 100 estados encontrados pelo agente. Sempre que é encontrado um estado que não está no conjunto armazenado, ele substitui aleatoriamente um estado armazenado com probabilidade de 0,01.

Os agentes exatos e UVFA têm taxas de desconto de 0,99 e 0,95, respectivamente. Para cada agente, fazemos uma busca em grade sobre o parâmetro de amplificação β (0,3, 1, 3, 10, 30, 100, 300, 1000), escolhendo o maior valor de β que permite que o agente receba a recompensa total na tarefa atual para agentes exatos (e pelo menos 90% da recompensa total para agentes UVFA). Reduzimos linearmente a taxa de exploração de 1 para 0 e a mantemos em 0 para os últimos 1000 episódios. Executamos os agentes por 50 mil episódios em todos os ambientes, exceto em Soko-coin, onde executamos os agentes exatos por 1 milhão de episódios e os agentes UVFA por 100 mil episódios. O tempo de execução do agente UVFA (em segundos por episódio) foi de 0,2 nos ambientes Soko-coin. Apenas a aproximação UVFA foi viável em Soko-coin-3, já que o método exato fica sem memória.

6.3. Resultados

Sushi. O agente sem recompensa auxiliar não tem incentivo para interferir no sushi e vai diretamente para a meta. Como o estado inicial é inatingível não importa o que o agente faça, a recompensa de reversibilidade é sempre 0, e então não produz comportamento de interferência. O agente de tarefa futura sem diretiva de linha de base interfere no sushi, enquanto o agente com diretiva de linha de base vai diretamente para a meta.

Vaso. Como o agente pode chegar à meta sem ações irreversíveis, tanto os métodos de reversibilidade quanto de tarefa futura evitam o efeito colateral neste ambiente, enquanto o agente regular quebra o vaso.

Caixa. O agente de reversibilidade perde sua recompensa auxiliar não importa como mova a caixa, e então ele segue o caminho mais rápido para a meta que empurra a caixa no canto (semelhante ao agente regular). No entanto, o agente de tarefa futura empurra a caixa para a direita, já que algumas tarefas futuras envolvem mover a caixa.

Soko-coin. Como o agente de reversibilidade perde sua recompensa auxiliar ao coletar moedas, ele empurra caixas próximas a paredes para chegar às moedas mais rápido (semelhante ao agente regular). No entanto, o agente de tarefa futura contorna as caixas para preservar tarefas futuras que envolvem mover caixas.

Os resultados são mostrados na Tabela 1. Cada agente de Q-learning exato convergiu para a diretiva ótima fornecida pela iteração de valor para a recompensa auxiliar correspondente. Apenas a abordagem das tarefas futuras com diretiva de linha de base se saiu bem em todos os ambientes, evitando efeitos colaterais e interferências. Embora a aproximação UVFA da recompensa auxiliar da tarefa futura evite efeitos colaterais de forma menos confiável do que a versão exata, ela mostra algum potencial para amplificar a abordagem das tarefas futuras.

7. Outros trabalhos relacionados

O critério dos efeitos colaterais usando características do estado. A consulta minimax-regret de Zhang et al. [2018] pressupõe um MDP fatorado no qual o agente pode alterar algumas das características e propõe um critério para consultar o supervisor sobre a alteração de outras características para permitir efeitos pretendidos. O RLSP de Shah et al. [2019] define uma recompensa auxiliar para evitar efeitos colaterais em termos de características do estado, pressupondo que o estado inicial do ambiente já esteja organizado de acordo com as preferências humanas. Embora essas abordagens sejam promissoras, elas requerem um conjunto de características do estado para calcular a recompensa auxiliar, o que aumenta o ônus sobre o projetista da recompensa.

Empoderamento. A abordagem das tarefas futuras está relacionada ao empoderamento [Klyubin et al., 2005, Salge et al., 2014], uma medida do controle do agente sobre seu ambiente. O empoderamento é definido como a máxima informação mútua entre as ações do agente e o estado futuro, e portanto mede a capacidade do agente de alcançar muitos estados de forma confiável. Maximizar o empoderamento incentivaria o agente a evitar efeitos colaterais irreversíveis, mas também incentivaria a interferência, e não nos está claro como definir uma medida baseada em empoderamento que evitaria isso. Uma possibilidade é penalizar a redução no empoderamento entre o estado atual s_T e o estado de referência s’_T. No entanto, o empoderamento é indiferente entre esses dois casos: A) os mesmos estados são alcançáveis a partir de s_T e s’_T, e B) um estado x é alcançável a partir de s’_T, mas não de s_T, enquanto outro estado y é alcançável a partir de s_T, mas não de s’_T. Assim, penalizar a redução no empoderamento poderia deixar passar alguns efeitos colaterais: p. ex., se o agente substituísse o sushi na esteira por um vaso, o empoderamento poderia permanecer o mesmo, e então o agente não seria penalizado por quebrar o vaso.

Exploração segura. Embora o problema da exploração segura possa parecer semelhante ao problema dos efeitos colaterais, a exploração segura se trata de evitar ações prejudiciais durante o processo de treinamento (um problema de aprendizado), enquanto o problema dos efeitos colaterais se trata de remover o incentivo para realizar ações prejudiciais (um problema de design de recompensa). Muitos métodos de exploração segura funcionam alterando os incentivos do agente e, portanto, potencialmente lidam com o problema dos efeitos colaterais. Isso inclui métodos de reversibilidade [Eysenbach et al., 2017], que evitam efeitos colaterais em tarefas que não requerem ações irreversíveis. Métodos de exploração segura que penalizam o risco [Chow et al., 2015] ou usam motivação intrínseca [Lipton et al., 2016] ajudam o agente a evitar efeitos colaterais que resultam em recompensas mais baixas (como ficar preso ou danificado), mas não desencorajam o agente a danificar o ambiente de maneiras que não são penalizadas pela função de recompensa (p. ex., quebrar vasos). Assim, os métodos de exploração segura oferecem soluções incompletas para os efeitos colaterais, assim como os métodos de efeitos colaterais fornecem soluções incompletas para a exploração segura. Esses métodos podem ser combinados, se desejado, para lidar com ambos os problemas.

Incerteza sobre a meta. O Design de Recompensa Inversa [Hadfield-Menell et al., 2017] incorpora incerteza sobre a meta considerando funções de recompensa alternativas que são consistentes com a função de recompensa fornecida no ambiente de treinamento e seguindo uma diretiva avessa ao risco. Isso ajuda a evitar efeitos colaterais decorrentes de mudanças na distribuição, nas quais o agente encontra um novo estado que não foi visto durante o treinamento. No entanto, além de evitar novos estados prejudiciais, o agente também evita novos estados benéficos. Outro método de incerteza é a quantilização [Taylor, 2016], que incorpora incerteza tirando amostras a partir do quantil superior de ações em vez de realizar a ação ótima. Essa abordagem não remove consistentemente o incentivo para efeitos colaterais, já que ações prejudiciais ainda serão retiradas como amostras algumas vezes.

Supervisão humana. Uma alternativa para especificar uma recompensa auxiliar é ensinar o agente a evitar efeitos colaterais por meio da supervisão humana, como o aprendizado por reforço inverso [Ng e Russell, 2000, Hadfield-Menell et al., 2016], demonstrações [Abbeel e Ng, 2004] ou o feedback humano [Christiano et al., 2017, Saunders et al., 2017]. Não está claro quão bem um agente pode aprender uma recompensa para evitar efeitos colaterais por meio da supervisão humana. Esperamos que isso dependa da diversidade de configurações nas quais ele recebe supervisão e sua capacidade de generalizar a partir dessas configurações, enquanto uma recompensa intrínseca para evitar efeitos colaterais seria mais resiliente e confiável. Uma recompensa auxiliar desse tipo também poderia ser combinada com a supervisão humana para diminuir a quantidade de entrada humana necessária para que um agente aprenda as preferências humanas, p. ex., se usada como uma probabilidade a priori para a função de recompensa aprendida.

8. Conclusões

Para enfrentar o desafio de definir o que são os efeitos colaterais, propusemos uma abordagem em que uma definição de efeitos colaterais é automaticamente inferida pela definição mais simples de metas futuras, o que estabelece uma base teórica para formalizar o problema dos efeitos colaterais. Essa abordagem fornece uma recompensa auxiliar para preservar a capacidade de realizar tarefas futuras, incentivando o agente a evitar os efeitos colaterais, independentemente de a tarefa atual exigir ações irreversíveis, e não introduz incentivos de interferência para o agente.

Existem muitas direções possíveis para trabalhos futuros, que incluem melhorar a aproximação do UVFA da recompensa da tarefa futura para evitar mais confiavelmente os efeitos colaterais, aplicar o método a agentes e ambientes mais complexos, generalizar a evasão de interferência para o caso estocástico, investigar a escolha da distribuição de tarefas futuras F (p. ex., incorporando preferências humanas por meio de métodos de feedback humano [Christiano et al., 2017]) e investigar outros possíveis incentivos indesejáveis que poderiam ser introduzidos além dos incentivos de interferência.

Impacto mais amplo

No aprendizado por reforço atual, o que o agente não deve fazer geralmente é especificado manualmente, p. ex., através de restrições ou recompensas negativas. Essa abordagem ad hoc dificilmente será amplificável para sistemas de IA mais avançados em ambientes mais complexos. As especificações ad hoc geralmente são incompletas e sistemas de IA mais capazes serão melhores em encontrar e explorar lacunas e brechas na especificação. Já vemos muitos exemplos de manipulação da especificação com os sistemas de IA atuais, e esse problema tende a piorar para sistemas de IA mais capazes [Krakovna et al., 2020].

Acreditamos que construir e implementar sistemas de IA mais avançados exige abordagens gerais e princípios de design para especificar objetivos do agente. Nosso artigo avança no desenvolvimento de um princípio geral, que visa capturar a heurística de “não causar danos” em termos das opções disponíveis no ambiente e dá ao agente um incentivo para considerar as consequências futuras de suas ações além da tarefa atual.

Sem uma maneira confiável e fundamentada de evitar mudanças desnecessárias no mundo, a implementação de sistemas de IA será limitada a domínios restritos nos quais o projetista pode enumerar tudo o que o agente não deve fazer. Assim, abordagens gerais para a especificação de metas possibilitariam à sociedade colher os benefícios da aplicação de sistemas de IA capazes a problemas mais difíceis, o que tem potencial para alto impacto a longo prazo.

Em termos de impactos negativos, adicionar uma recompensa auxiliar para tarefas futuras aumenta os requisitos computacionais e, consequentemente, o custo de energia do treinamento de algoritmos de aprendizado por reforço, em comparação com recompensas projetadas manualmente e restrições para evitar efeitos colaterais. As lacunas restantes nos fundamentos teóricos de nosso método poderiam levar a problemas inesperados se não forem pesquisadas adequadamente e em vez disso deixadas para a avaliação empírica.

Agradecimentos

Agradecemos a Ramana Kumar pelo feedback detalhado e construtivo nos rascunhos do artigo e no código. Também agradecemos a Jonathan Uesato, Matthew Rahtz, Alexander Turner, Carroll Wainwright, Stuart Armstrong e Rohin Shah pelo feedback útil nos rascunhos.

Notas

1. Código: github.com/deepmind/deepmind-research/tree/master/side_effects_penalties

Referências

Consulte as referências do documento orginal.

---

Tradução: Luan Marques

Link para o original